Privacy & Cookies
Deze site maakt gebruik van cookies. Door verder te gaan, gaat u akkoord met het gebruik ervan. Lees meer, inclusief hoe u cookies kunt beheren.
Een spiraal is een kromme die “uitgaat van een punt en zich verder verwijdert naarmate hij om het punt draait”.

Er zijn veel verschillende soorten spiralen, afhankelijk van de formules waarmee ze zijn gemaakt. In deze blogpost zal ik tweedimensionale spiralen bespreken (merk op dat er ook een verscheidenheid aan driedimensionale spiralen bestaat).
Archimedeese Spiraal
Dit is een spiraal genoemd naar de beroemde Griekse wiskundige Archimedes, die de eerste was die deze beschreef in zijn boek Over spiralen. Zij wordt beschreven door de volgende poolvergelijking:
waarbij a en b reële getallen zijn.
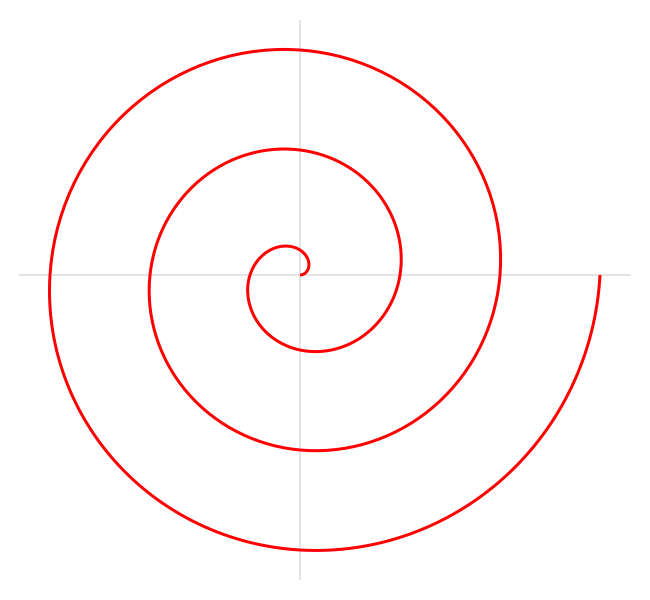
Door parameter a te veranderen zal de spiraal draaien en parameter b bepaalt de afstand tussen opeenvolgende draaiingen.
De spiraal van Fermat
De spiraal van Fermat is een parabolische spiraal die aan de volgende poolvergelijking voldoet:
Het is een soort Archimedische spiraal.

Eulerspiraal
Zogenaamd Cornu-spiraal, is een kromme waarvan de kromming toeneemt naarmate de afstand tot de oorsprong groter wordt; “de kromming van een cirkelvormige kromme is gelijk aan het reciproke van de straal”.

De parametervorm bestaat uit twee vergelijkingen met de intervallen van Fresnel, die slechts bij benadering kunnen worden opgelost.
Deze integralen, en daarmee de Eulerspiraal, kunnen worden gebruikt om de energieverdeling van de diffractie van Fresnel bij een enkel spleetje in de golftheorie te beschrijven.
Hyperbolische spiraal
De hyperbolische spiraal, voor het eerst bedacht door Pierre Varignon in 1704, is een transcendentale kromme, wat betekent dat “het een analytische functie is die niet aan een veeltermvergelijking voldoet”. Zij is het tegengestelde van een Archimedespiraal en heeft dus de volgende poolvergelijking:
In het centrum bevindt zij zich op oneindige afstand van de pool; voor θ beginnend bij 0, begint r bij oneindig.
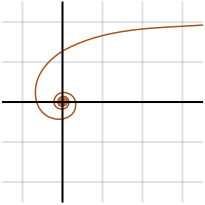
Lituus
De lituus is een spiraal met een poolvergelijking:
waarbij k een constante is. De hoek is dus omgekeerd evenredig met het kwadraat van de straal. 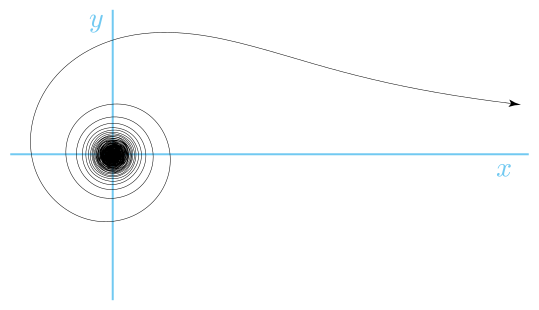
De kromme is genoemd naar de oude Romeinse lituus (een gebogen augurale staf of oorlogstrompet) door Roger Cotes in een verzameling verhandelingen gepubliceerd in 1722.
Logaritmische spiraal
 De logaritmische spiraal is een zelfgelijkvormige spiraal, die vaak in de natuur voorkomt. Zij werd voor het eerst beschreven door Descartes, maar werd diepgaand bestudeerd door Jacob Bernoulli, die haar “de wonderbaarlijke spiraal” noemde. Hij heeft een poolvergelijking van
De logaritmische spiraal is een zelfgelijkvormige spiraal, die vaak in de natuur voorkomt. Zij werd voor het eerst beschreven door Descartes, maar werd diepgaand bestudeerd door Jacob Bernoulli, die haar “de wonderbaarlijke spiraal” noemde. Hij heeft een poolvergelijking van





Geef een antwoord