mishadoff gedachten

Implementeren van Depth-First Search voor de Binaire Boom zonder stack en recursie.

Binaire Boom Array

Dit is een binaire boom.

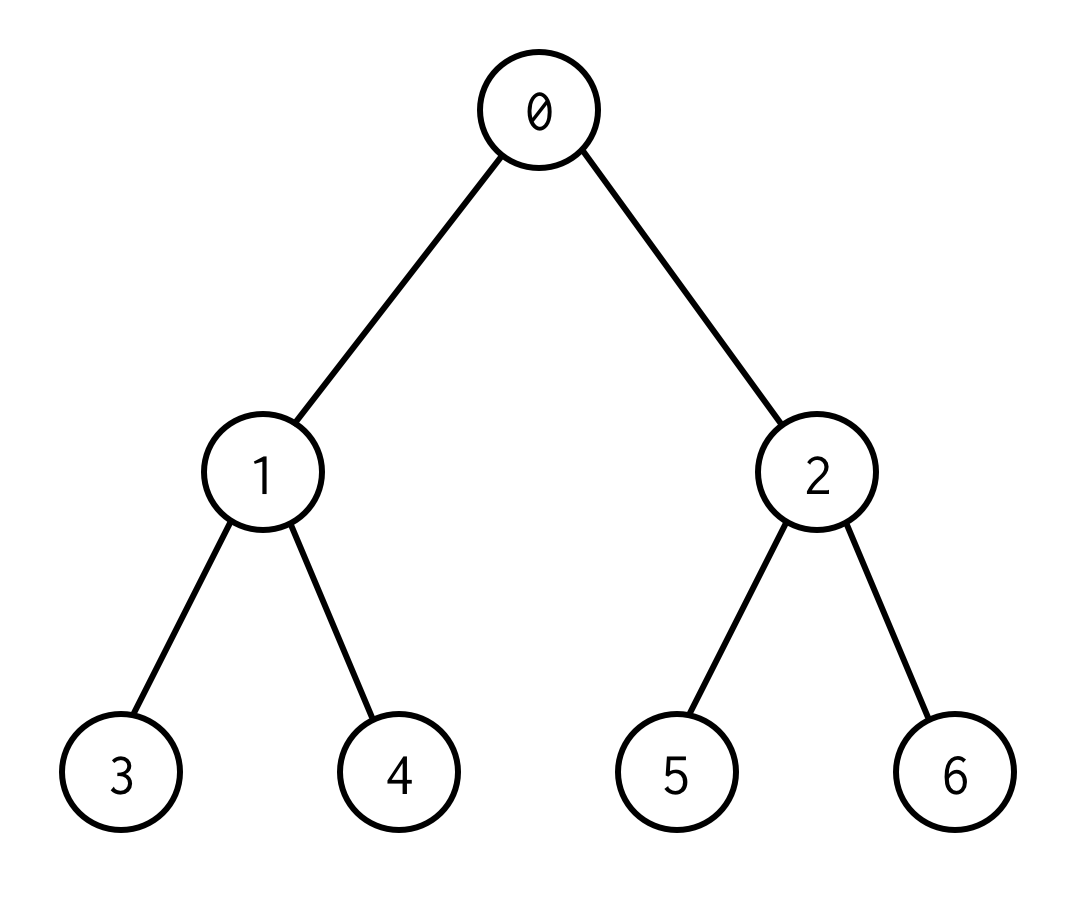
0 is een wortelknooppunt.
0 heeft twee kinderen: links 1 en rechts: 2.
Elke van zijn kinderen heeft zijn kinderen enzovoort.
De knooppunten zonder kinderen zijn bladknooppunten (3,4,5,6).

Het aantal randen tussen wortel- en bladknooppunten bepaalt de hoogte van de boom.De boom hierboven heeft de hoogte 2.

Standaardmethode om een binaire boom te implementeren is het definiëren van een klasse genaamd BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Echter, er is een truc om een binaire boom te implementeren door alleen statische arrays te gebruiken. Als u alle knooppunten in een binaire boom opsommt door niveaus te beginnen vanaf nul, kunt u deze in een array verpakken.

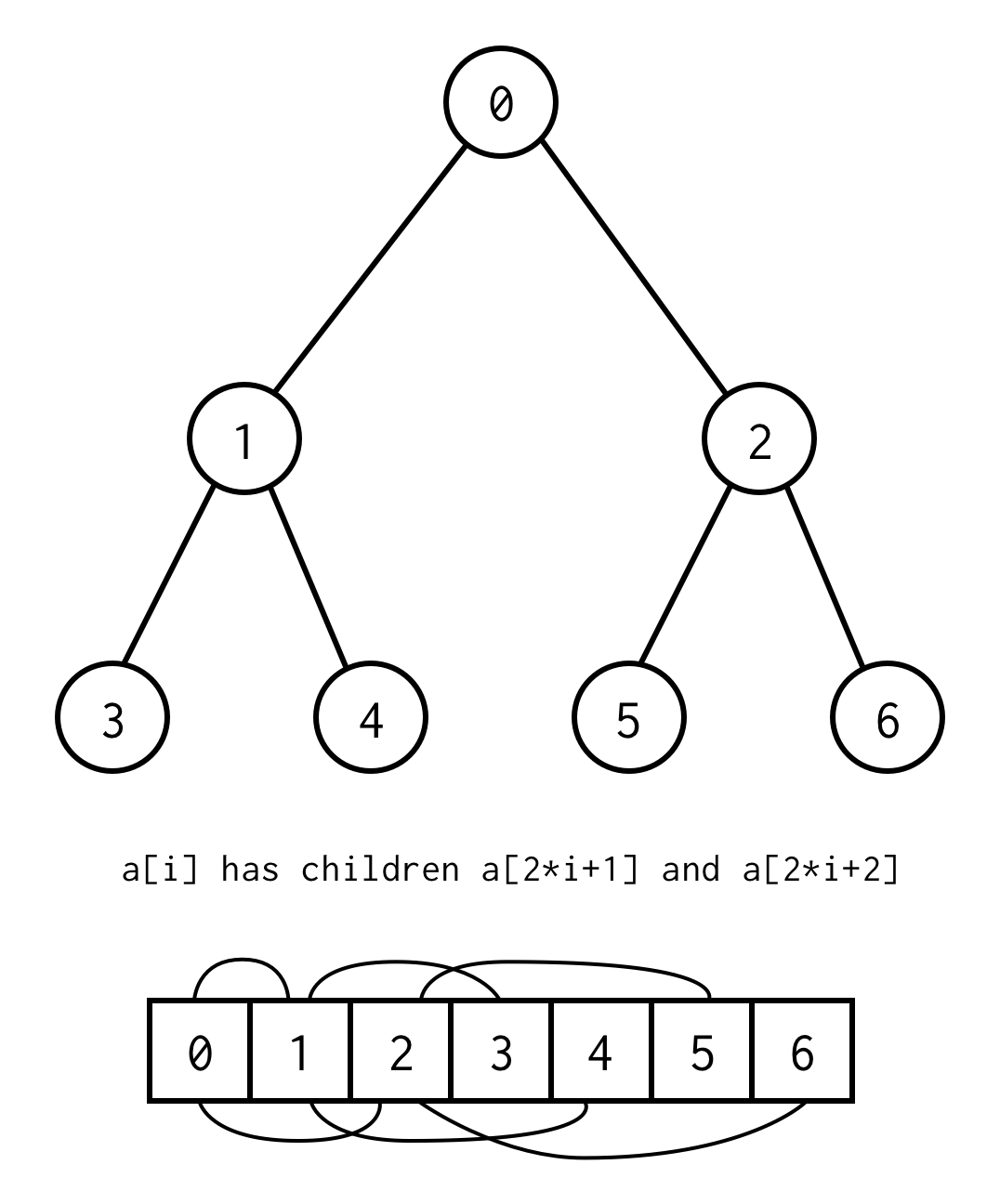
De relatie tussen ouderindex en kindindex, laat ons toe om van de ouder naar het kind te gaan, alsook van het kind naar de ouder

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Belangrijke opmerking is dat de boom volledig moet zijn, wat betekent dat hij voor de specifieke hoogte precies elementen moet bevatten.

U kunt deze eis omzeilen door null te plaatsen in plaats van ontbrekende elementen.De opsomming geldt ook nog steeds voor lege knooppunten. Dit zou elke mogelijke binaire boom moeten dekken.

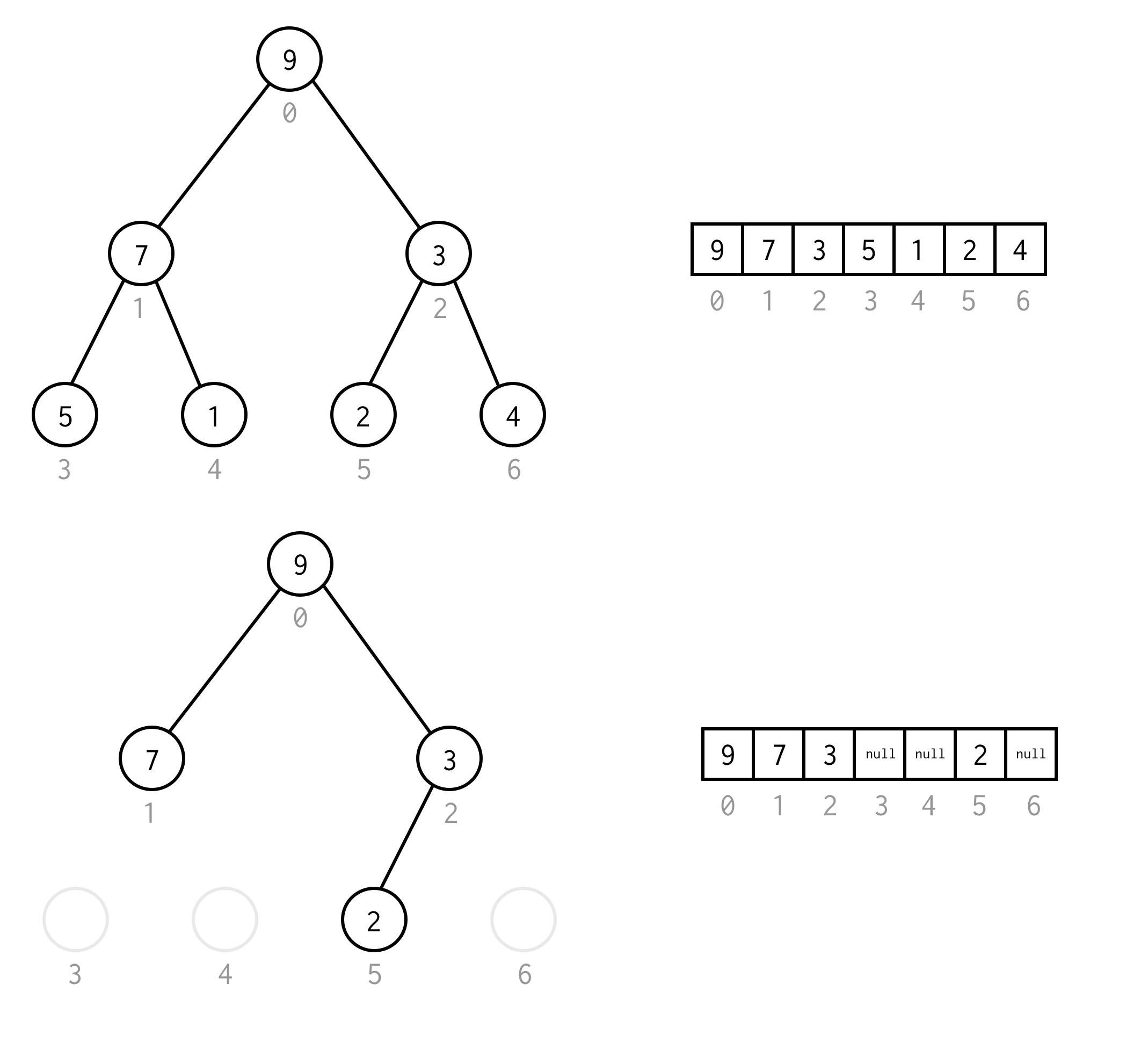
Zulke array-weergave voor binaire bomen noemen we Binary Tree Array.We gaan er altijd van uit dat deze elementen zal bevatten.

BFS vs DFS

Er bestaan twee zoekalgoritmen voor binaire bomen: breadth-first search (BFS) en depth-first search (DFS).

De beste manier om ze te begrijpen is visueel

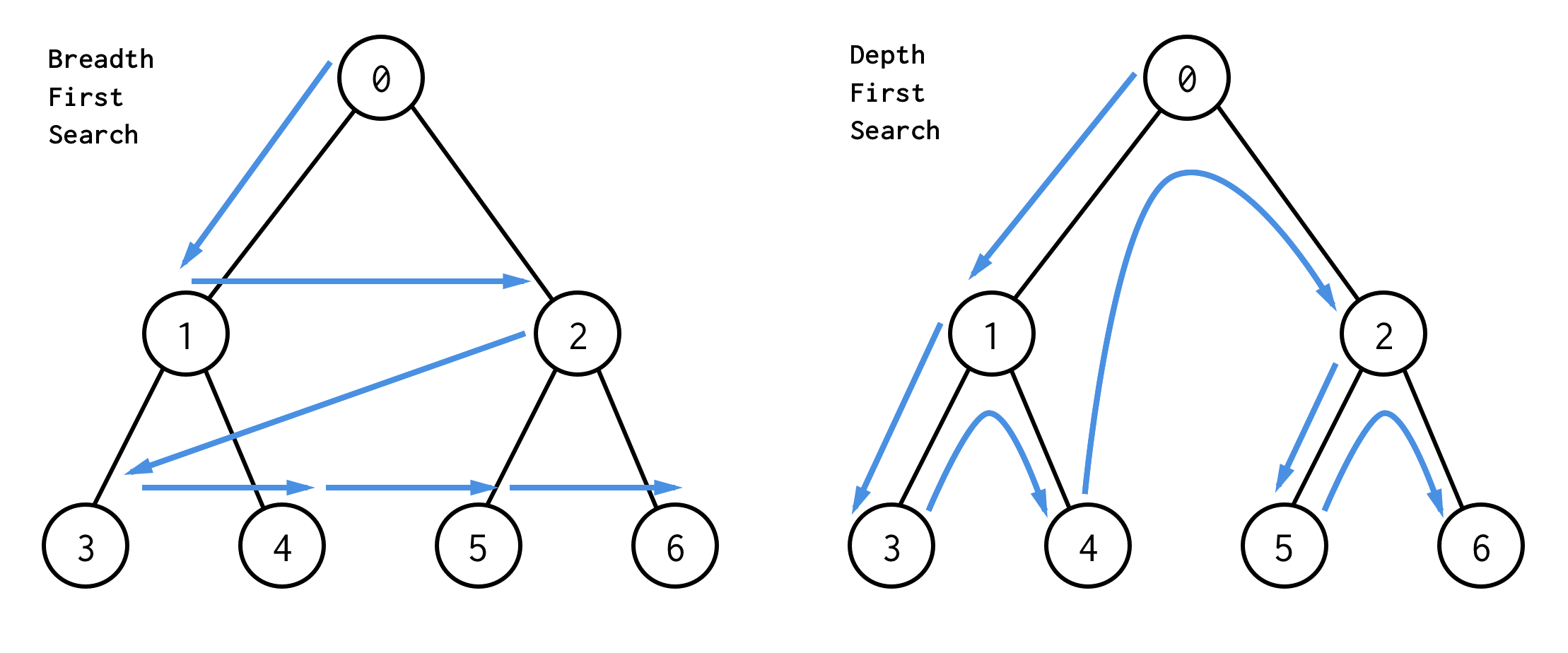
BFS doorzoekt knooppunten niveau per niveau, beginnend bij de wortelknoop. Dan worden de kinderen gecontroleerd. Totdat alle knooppunten zijn verwerkt of een knooppunt is gevonden dat aan de zoekvoorwaarde voldoet.

DFS gedraagt zich anders. Het controleert alle knooppunten vanaf het meest linkse pad van de wortel naar het blad, springt dan omhoog en controleert het meest rechtse knooppunt enzovoort.

Voor klassieke binaire bomen is BFS geïmplementeerd met behulp van een wachtrij-gegevensstructuur (LinkedList implementeert wachtrij)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Als u wachtrij vervangt door stapel, krijgt u DFS-implementatie.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Bij wijze van voorbeeld, stel dat u een knooppunt met de waarde 1 in de volgende boom moet vinden.

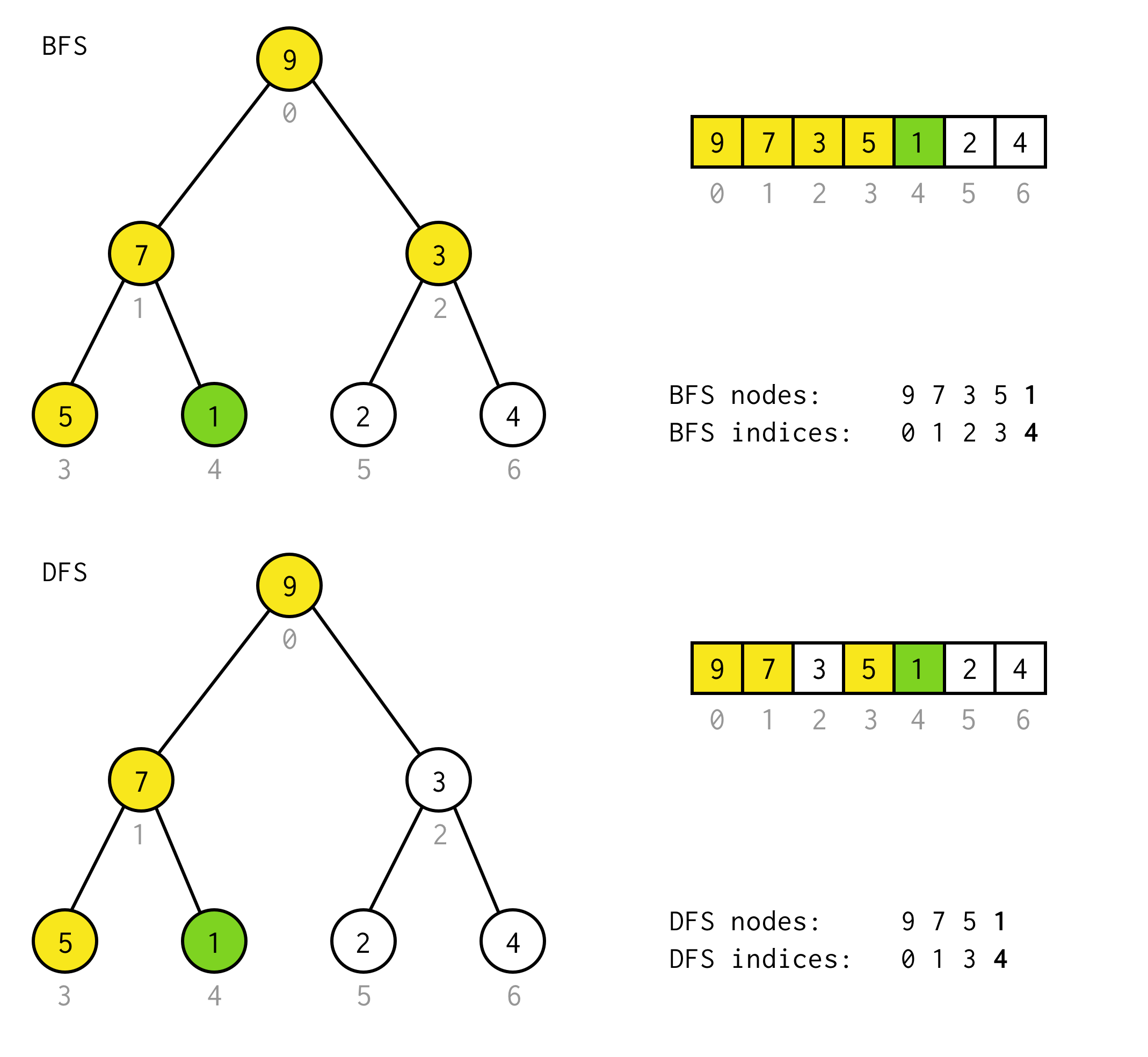
Gele cellen zijn cellen die in het zoekalgoritme worden getest voordat het benodigde knooppunt is gevonden.Houd er rekening mee dat DFS in sommige gevallen minder knooppunten nodig heeft voor verwerking.In sommige gevallen zijn er meer nodig.

BFS en DFS voor Binary Tree Array

Breadth-first search voor binary tree array is triviaal.Aangezien elementen in binary tree array niveau per niveau worden geplaatst en bfs ook elementen niveau per niveau controleert, is bfs voor binary tree array gewoon lineair zoeken

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

Depth-first search is een beetje moeilijker.

Gebruik makend van een stack datastructuur kan het op dezelfde manier worden geïmplementeerd als voor een klassieke binaire boom, gewoon indexen in de stack plaatsen.

Van hieruit is recursie helemaal niet anders, je gebruikt gewoon een impliciete methode-aanroep stack in plaats van een datastructuur stack.

Wat als we DFS zouden kunnen implementeren zonder stack en recursie.Uiteindelijk is het gewoon een juiste index selecteren bij elke stap?

Wel, laten we het proberen.

DFS voor Binary Tree Array (zonder stack en recursie)

Zoals in BFS beginnen we bij de wortelindex 0.
Dan moeten we zijn linker kind inspecteren, welke index kan worden berekend door formule 2*i+1.
Laten we het proces om naar het volgende linker kind te gaan verdubbelen.

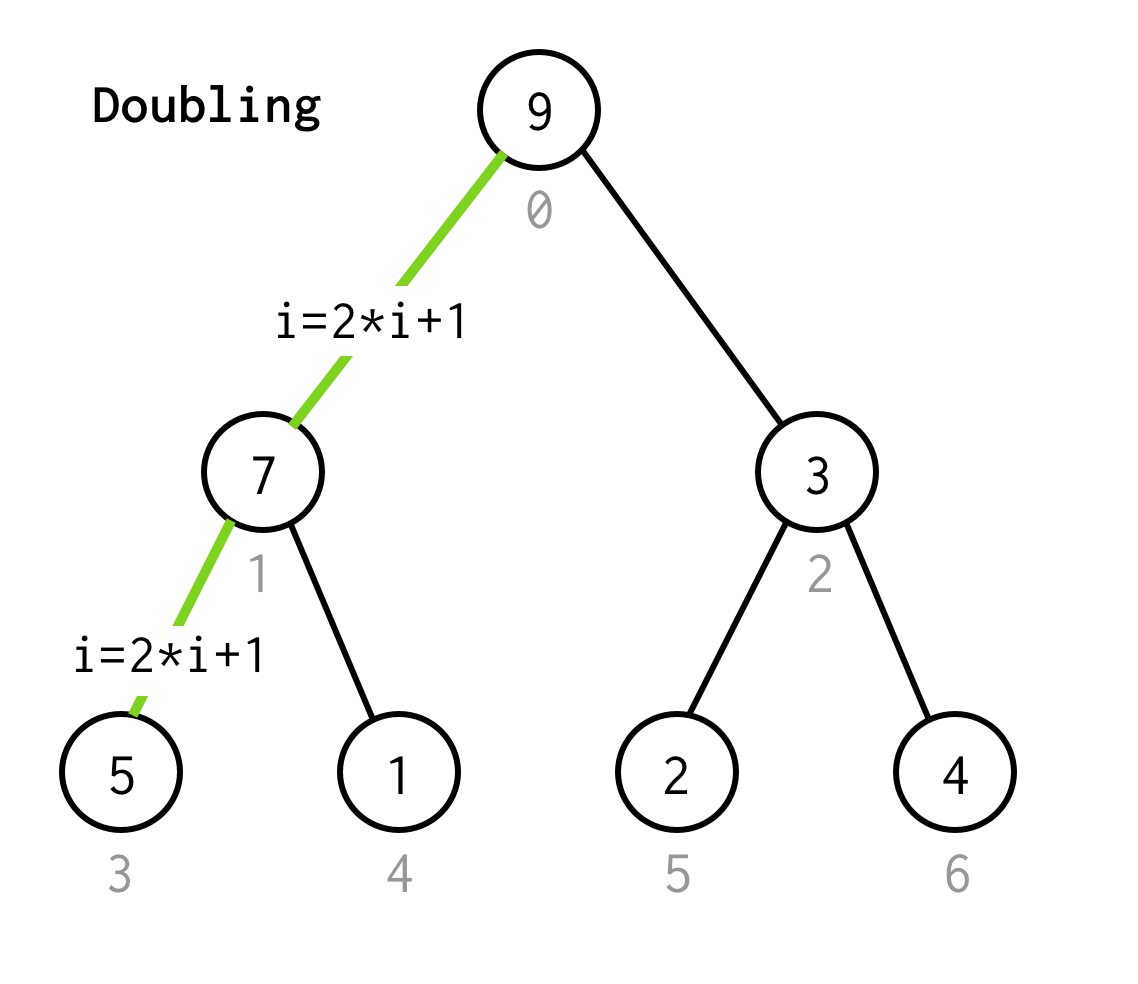
We blijven de index verdubbelen totdat we niet stoppen bij het bladknooppunt.

Dus hoe kunnen we begrijpen dat het een bladknooppunt is?

Als het volgende linker kind een exceptie produceert dat de index buiten de grenzen van de array valt, moeten we stoppen met verdubbelen en naar het rechter kind springen.

Dat is een geldige oplossing, maar we kunnen onnodige verdubbelingen vermijden.De observatie hier is dat het aantal elementen in de boom van sommige height twee keer zo groot is (en plus één)als de boom met height - 1.

Voor een boom met height = 2 hebben we 7 elementen, voor een boom met height = 3 hebben we 7*2+1 = 15 elementen.

Gebruik makend van deze observatie bouwen we een eenvoudige voorwaarde

i < array.length / 2

U kunt controleren of deze voorwaarde geldig is voor elk niet-bladig knooppunt in de boom.

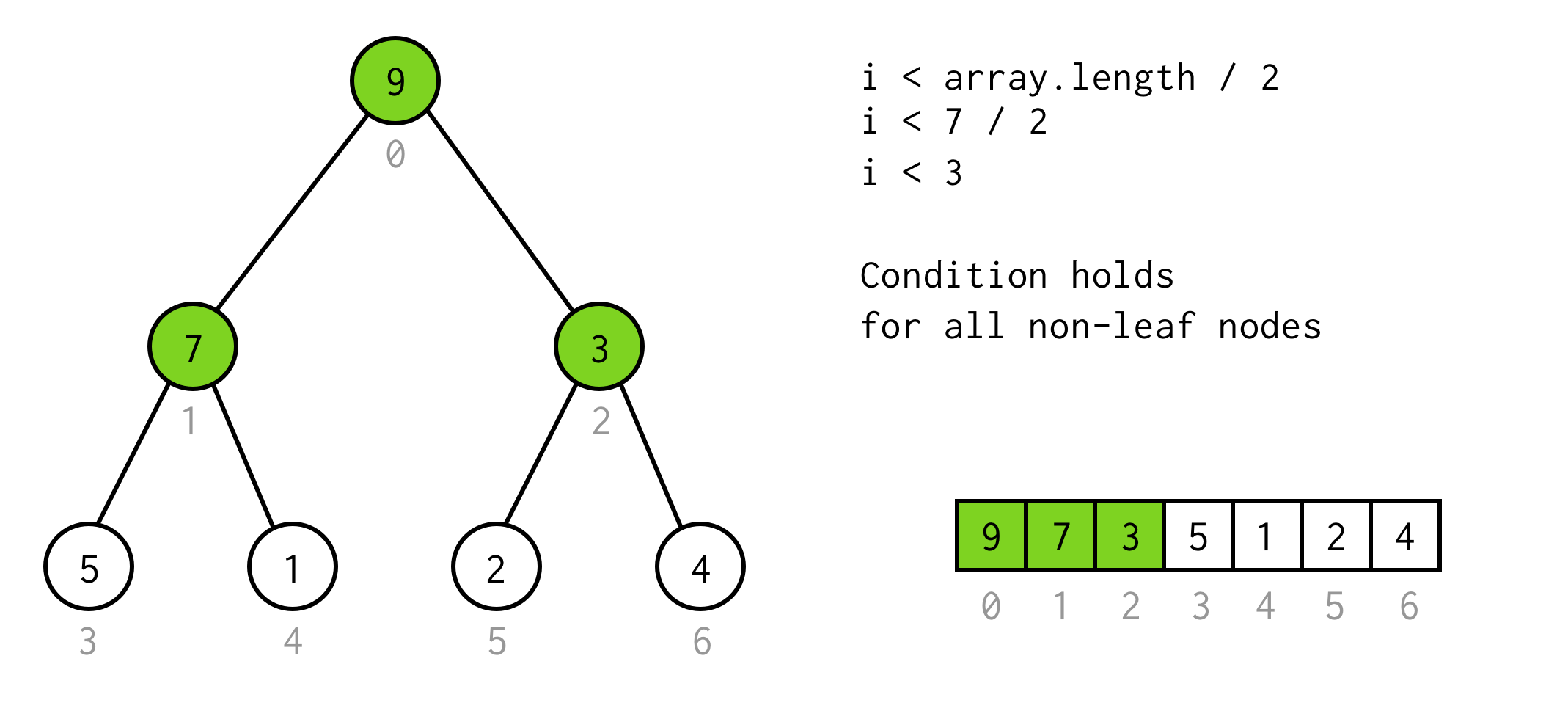
Mooi tot zover. We kunnen verdubbelen, en we weten zelfs wanneer we moeten stoppen. Maar op deze manier kunnen we alleen de linker kinderen van de nodes controleren.

Wanneer we vastzitten bij de blad node en geen verdubbeling meer kunnen toepassen, voeren we een sprong operatie uit.In principe, als verdubbelen is naar het linker kind gaan, is springen naar ouder gaan en naar het rechter kind gaan.

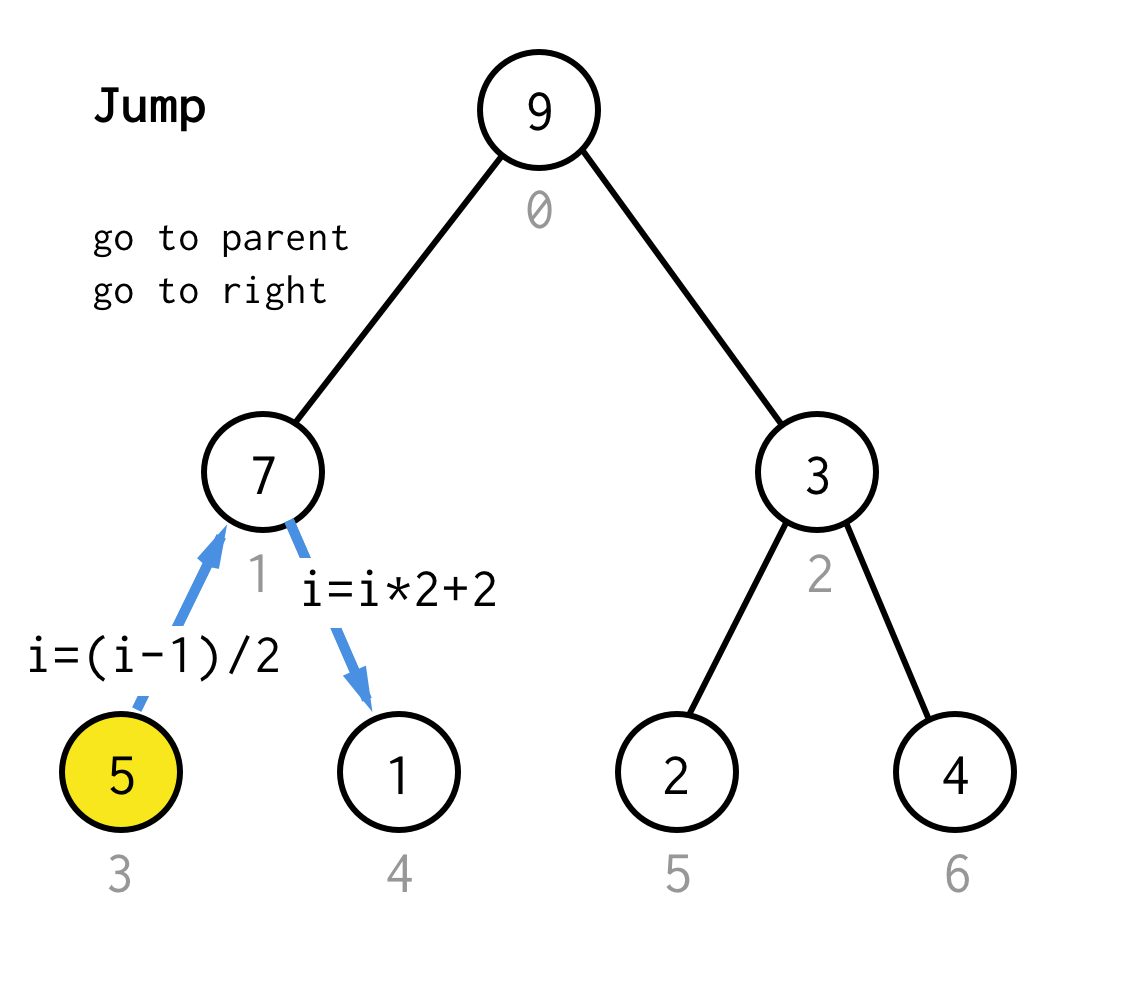
Zulke sprongoperatie kan worden geïmplementeerd door alleen de bladindex te verhogen. Maar als we vastzitten bij het volgende bladknooppunt, verplaatst de verhoging het knooppunt niet naar het volgende knooppunt, wat vereist is voor DFS.Dus moeten we een dubbele sprong uitvoeren

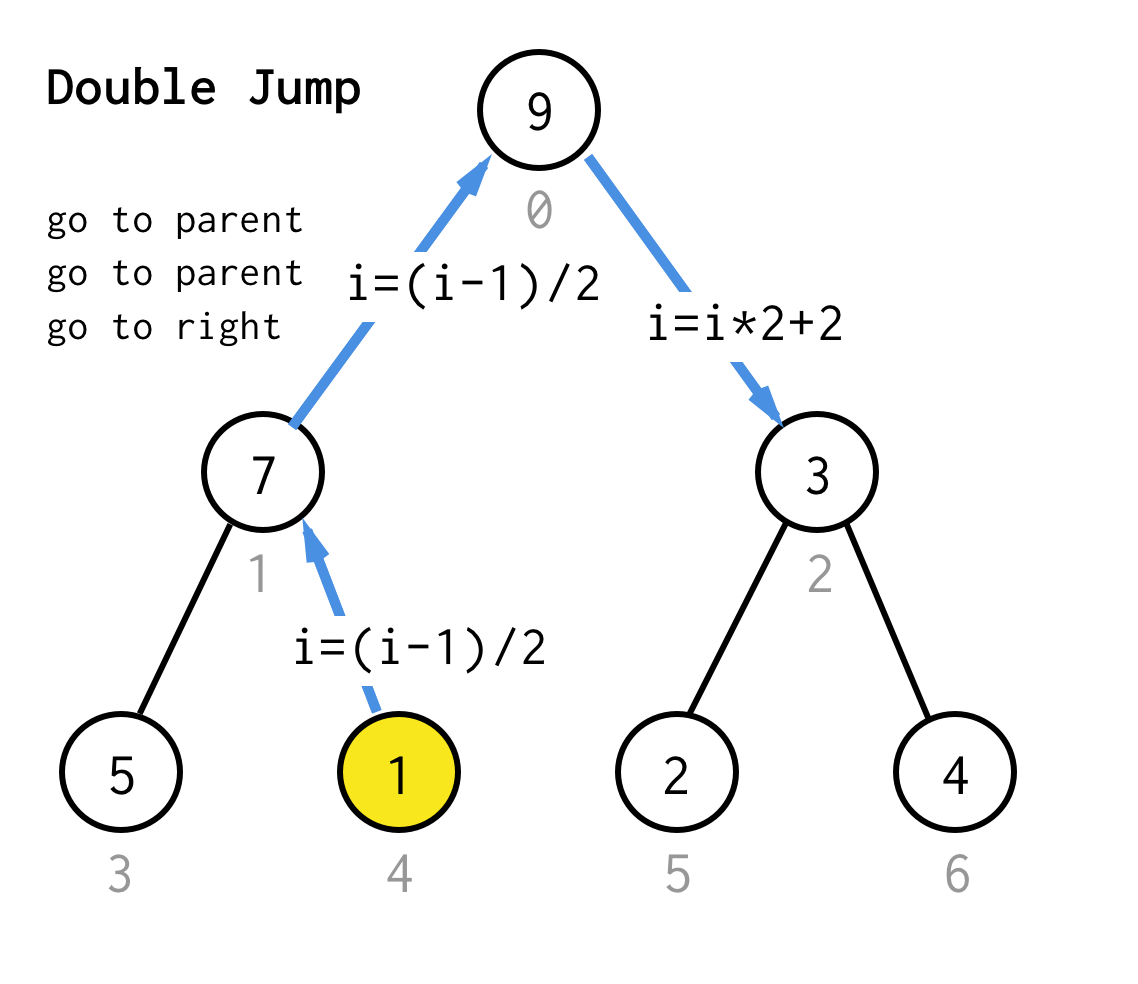
Om het meer generiek te maken, zouden we voor ons algoritme de operatie sprong N kunnen definiëren, die specificeert hoeveel sprongen naar de ouder nodig zijn en altijd eindigt met één sprong naar het juiste kind.

Voor de boom met hoogte 1, hebben we één sprong nodig, sprong 1

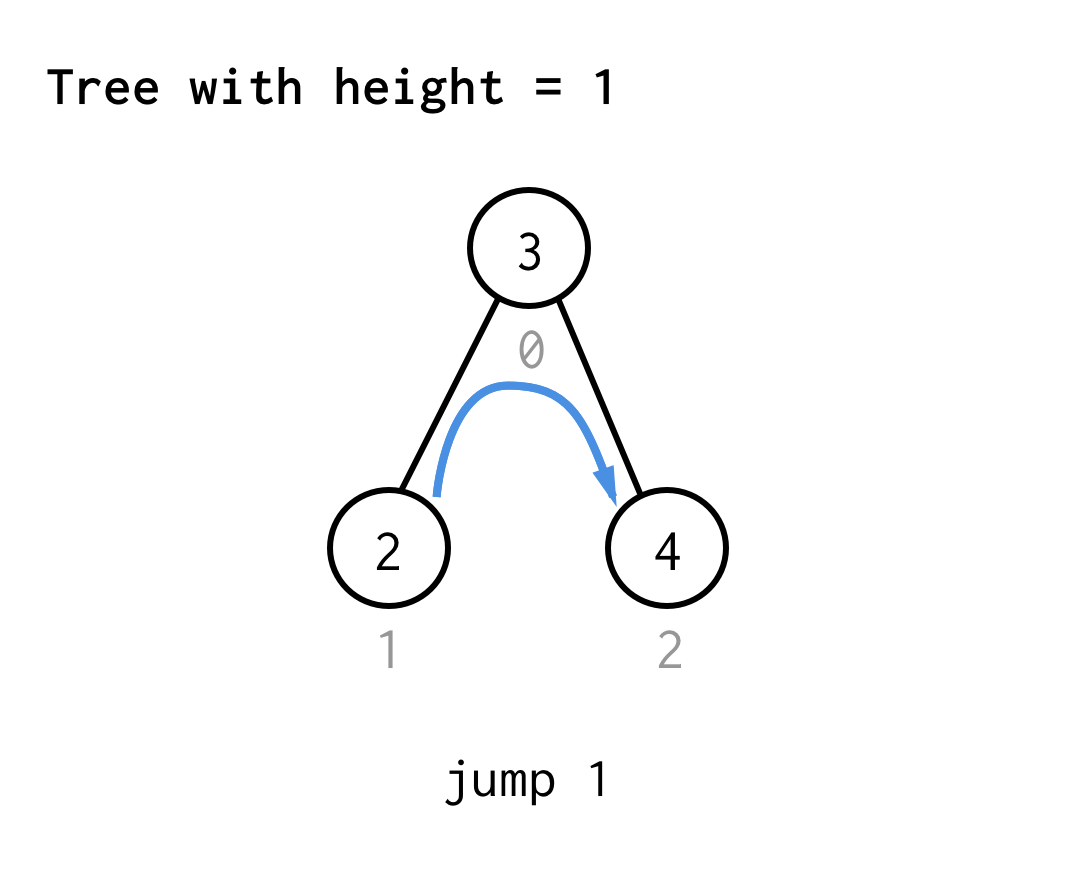
Voor de boom met hoogte 2, hebben we één sprong nodig, één dubbele sprong, en dan weer één sprong

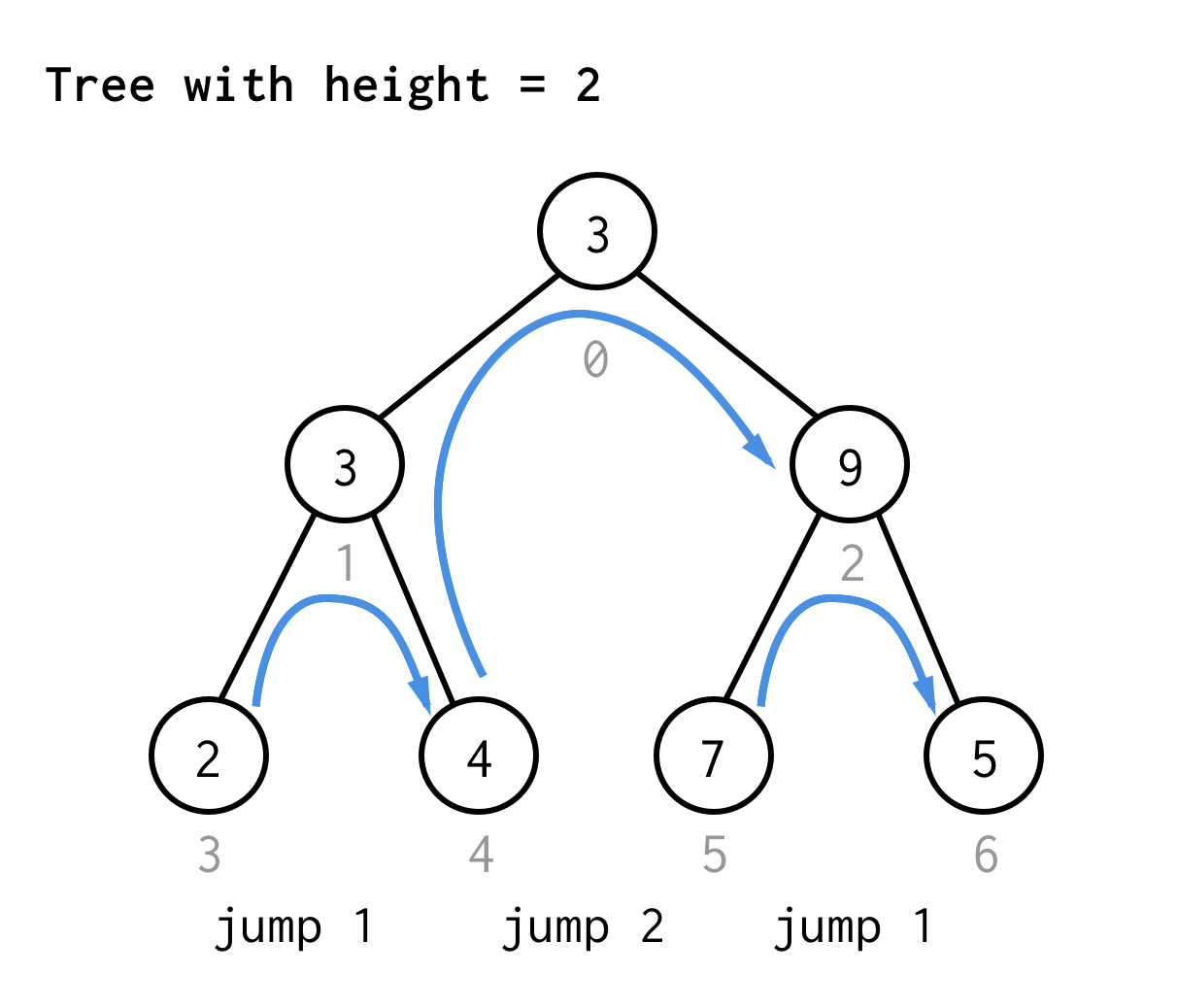
Voor de boom met hoogte 3, kunt u dezelfde regels toepassen en 7 sprongen krijgen.

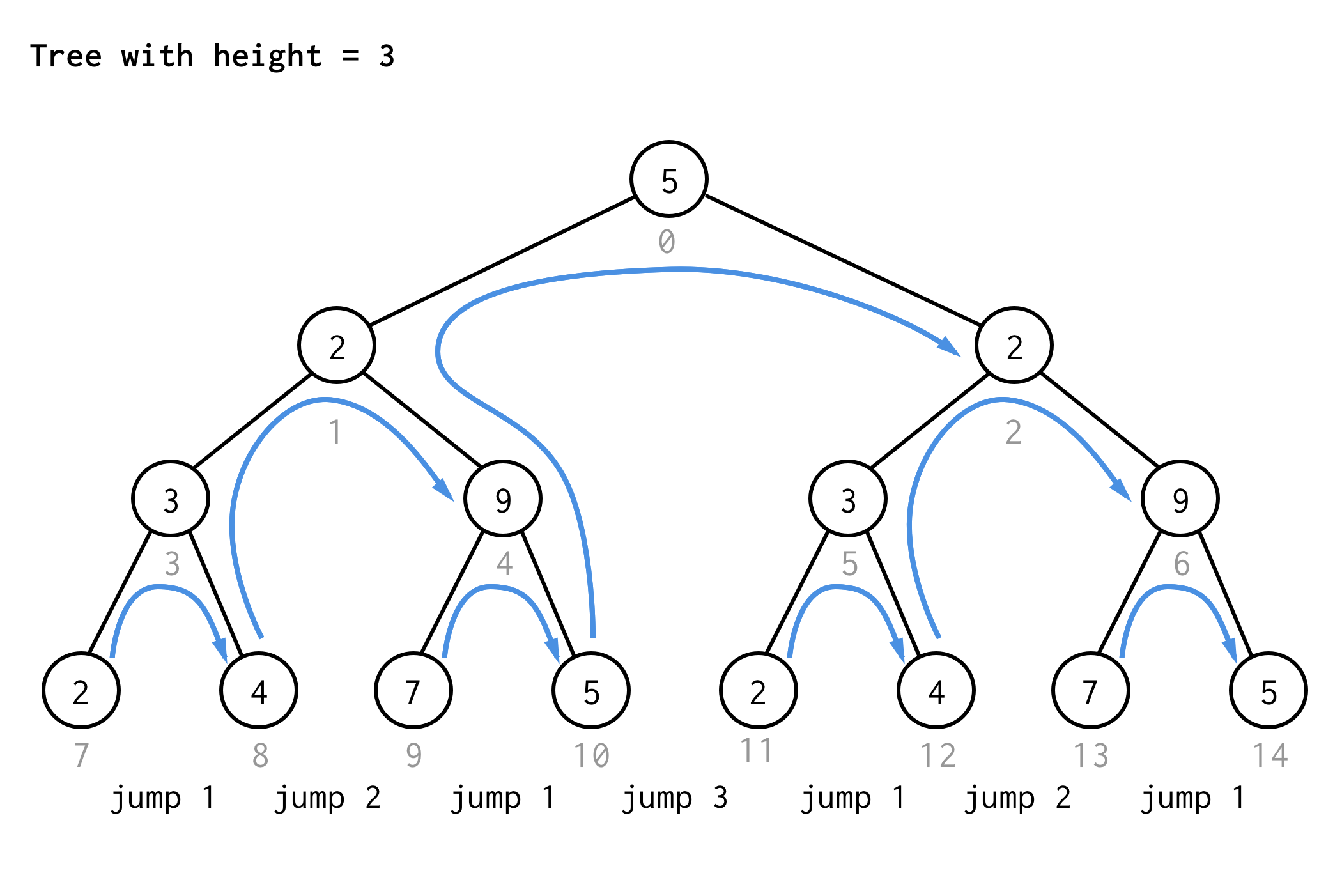
Zie u het patroon?

Als u dezelfde regel toepast op de boom met hoogte 4 en alleen sprongwaarden noteert, krijgt u het volgende volgnummer

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Deze reeks staat bekend als Zimin woorden en heeft een recursieve definitie, wat niet geweldig is, omdat we geen recursie mogen gebruiken.

Laten we een andere manier vinden om het te berekenen.

Als u goed kijkt naar de sprongreeks, ziet u een niet recursief patroon.

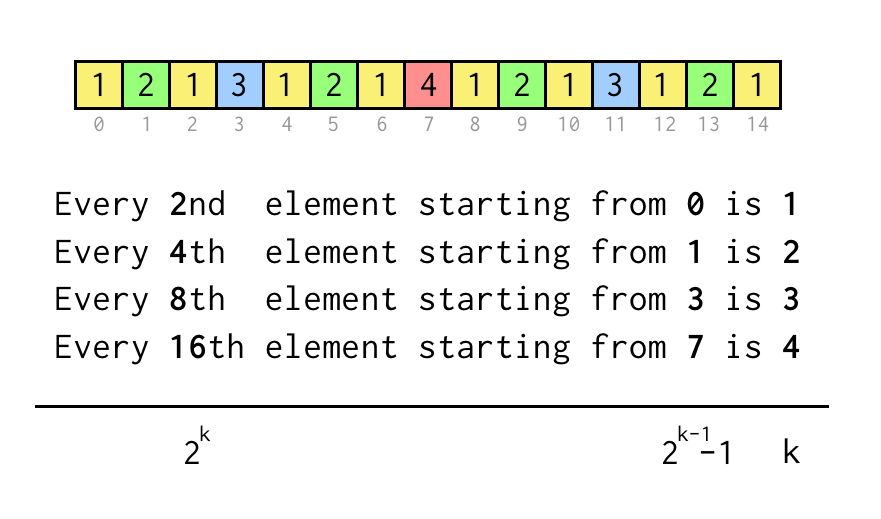
We kunnen de index voor het huidige blad j volgen, die overeenkomt met de index in de reeksreeks hierboven.

Om een bewering als “Elk 8e element vanaf 3” te controleren, hoeven we alleen maar j % 8 == 3 te controleren, en als dat waar is, springen we met drie sprongen naar het gewenste bovenliggende knooppunt.

Iteratief spring proces zal het volgende zijn

• Begin met k = 1
• Spring eenmaal naar de ouder door i = (i - 1)/2
• Als leaf % 2*k == k - 1 alle sprongen zijn uitgevoerd, exit
• Of anders, zet k op 2*k en herhaal.

Als u alles samenvoegt wat we hebben besproken

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Gedaan. DFS voor binaire boom array zonder stack en recursie

Complexiteit

De complexiteit lijkt kwadratisch omdat we lus in een lus hebben, maar laten we eens kijken wat de werkelijkheid is.

• Voor de helft van de totale knopen (n/2) gebruiken we verdubbelingsstrategie, die constant is O(1)
• Voor de andere helft van de totale knopen (n/2) gebruiken we bladsprongstrategie.
• De helft van de bladspringende knopen (n/4) vereisen slechts één oudersprong, 1 iteratie. O(1)
• De helft van deze helft (n/8) vereisen twee sprongen, of 2 iteraties. O(1)
• …
• Een enkel blad springend knooppunt vereist een volledige sprong naar de wortel, dat is O(logN)
• Dus, als alle gevallen O(1) hebben behalve een die O(logN) is, kunnen we zeggen dat het gemiddelde voor de sprong O(1)
• Totale complexiteit is O(n)

Prestatie

Hoewel de theorie goed is, laten we eens kijken hoe dit algoritme in de praktijk werkt, vergeleken met anderen.

We testen 5 algoritmen, met JMH.

• BFS op Binary Tree (gekoppelde lijst als wachtrij)
• BFS op Binary Tree Array (lineair zoeken)
• DFS op Binary Tree (stack)
• DFS op Binaire Boom Array (stack)
• Iteratieve DFS op Binaire Boom Array

We hebben een boom gemaakt en gebruiken een predikaat om het laatste knooppunt te vinden,om er zeker van te zijn dat we altijd hetzelfde aantal knooppunten raken voor alle algoritmes.

Dus, resultaten

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Het is duidelijk dat BFS op array wint. Het is gewoon een lineaire zoekactie, dus als je een binaire boom als array kunt representeren, doe het dan.

Iteratief DFS, dat we net in het artikel beschreven, nam 2 de tweede plaats in en 4.5 keer langzamer dan lineair zoeken (BFS op array)

De overige drie algoritmen zijn nog langzamer dan iteratief DFS, waarschijnlijk, omdat er extra datastructuren, extra ruimte en geheugentoewijzing bij komen kijken.

En het ergste geval is BFS op Binary Tree. Ik vermoed dat hier de gelinkte lijst een probleem is.

Conclusie

Binary Tree Array is een mooie truc om hiërarchische datastructuren te representeren als een statische array (aaneengesloten gebied in het geheugen). Het definieert een eenvoudige index-relatie om van ouder naar kind te gaan, en ook om van kind naar ouder te gaan, wat niet mogelijk is met een klassieke binaire array representatie. Er zijn enkele nadelen, zoals langzaam invoegen/verwijderen, maar ik weet zeker dat er genoeg toepassingen zijn voor binaire boom-arrays.

Zoals we hebben laten zien, zijn zoek-algoritmen, BFS en DFS geïmplementeerd op arrays veel sneller dan hun broertjes op een referentie-gebaseerde structuur. Voor echte wereldproblemen is dat niet zo belangrijk, en waarschijnlijk zal ik nog steeds de referentie-gebaseerde binaire array gebruiken.

Hoe dan ook, het was een leuke excercitie. Verwacht vraag “DFS op binaire array zonder recursie en stack” op uw volgende interview.

• algoritmen
• datastructuren
• programmeren

mishadoff 10 september 2017