バイナリツリーに対してスタックや再帰を使わない深さ優先探索を実装する。
Binary Tree Array
これはバイナリツリーです。
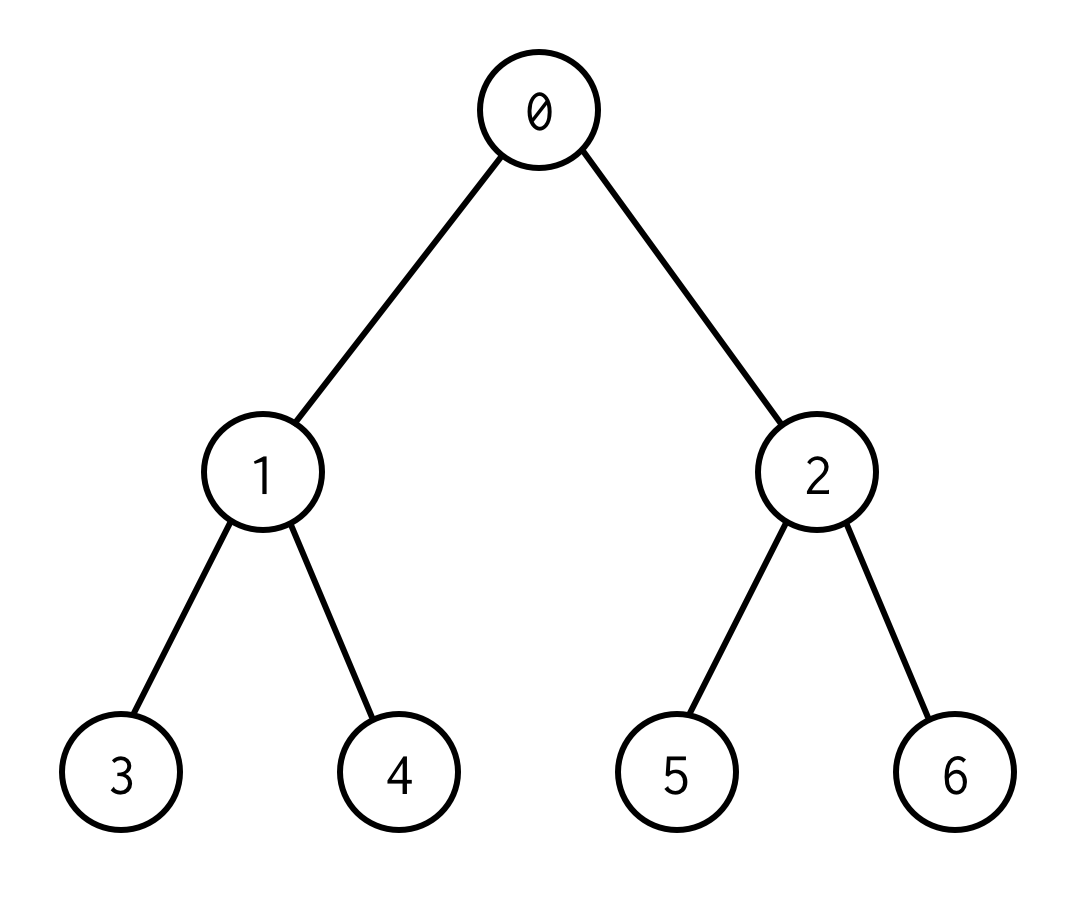
0 はルートノードです。 0 には左 1 と右という二つの子供がいます。 0 はleft 1 とright 2 の2つの子を持ち、その子はさらにその子を持つ。
子のないノードは葉ノード (3,4,5,6) 。
ルートと葉ノード間の辺数で木の高さが決まり、上記の木は 2 高さとなる。
二分木の標準的な実装方法は、BinaryNode
public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}というクラスを定義することですが、静的配列だけで実装する裏技が存在します。
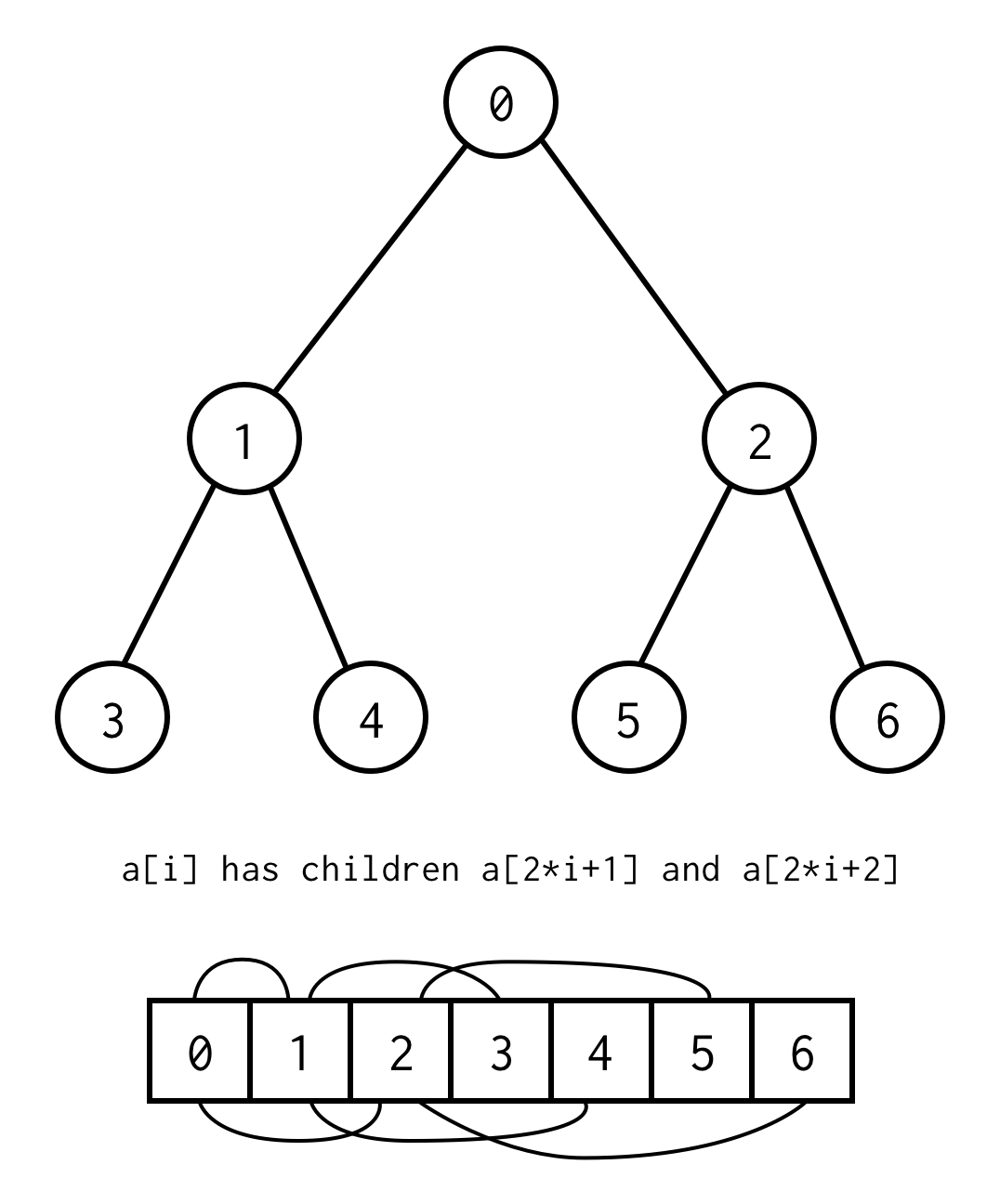
親インデックスと子インデックスの関係により、親から子へ、子から親へ移動できる
left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2重要なのは、木は完全でなければならないということ、つまり特定の高さに正確に要素を含んでいなければならないということだ。
欠落した要素の代わりに null を配置することで、この要件を回避することができます。
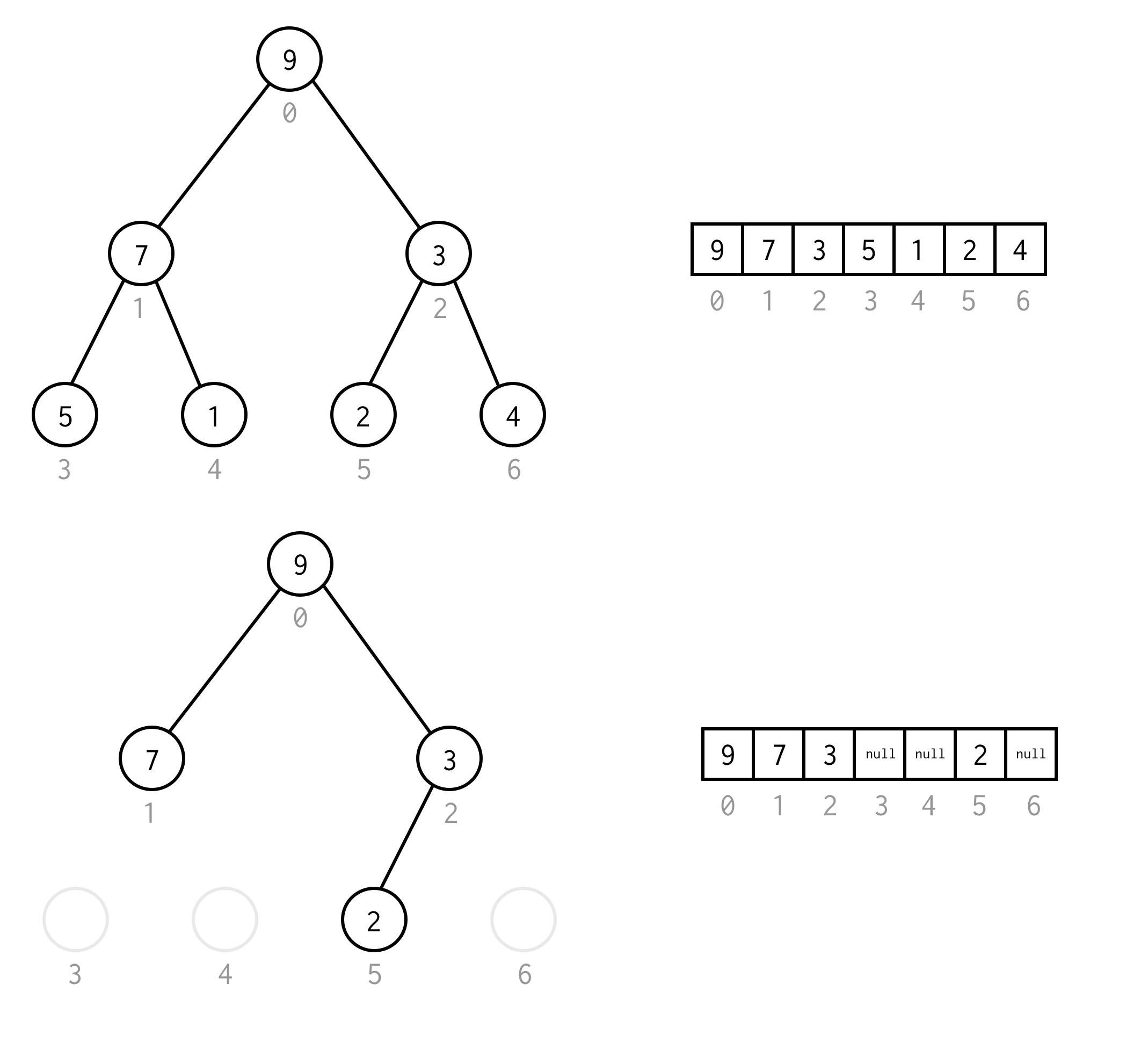
このような二分木の配列表現を二分木配列と呼び、常に要素を含むと仮定する。
BFS vs DFS
二分木の探索アルゴリズムには、幅優先探索 (BFS) と深さ優先探索 (DFS) があります。 次に、その子をチェックします。 すべてのノードを処理するか、検索条件を満たすノードを見つけるまで、子ノード、子ノード、子ノードの順に検索を続ける。 7809>
古典的な2分木のBFSはQueueデータ構造(LinkedListはQueueを実装)を使って実装されています。
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}例えば、以下の木から値1のノードを見つける必要があるとします。
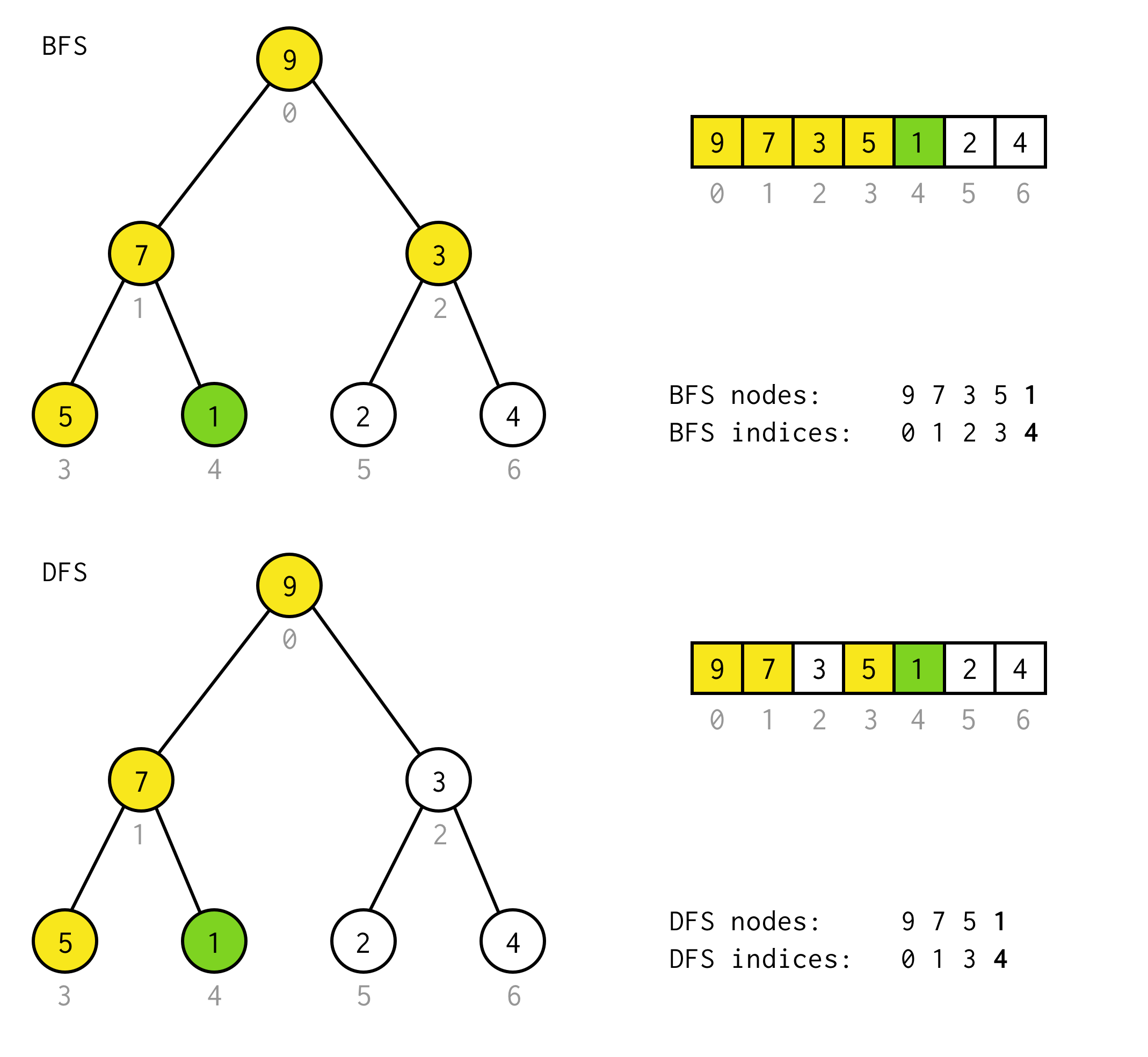
黄色のセルは検索アルゴリズムでテストされるノードで、目的のノードを見つける前にテストします。7809>
BFS and DFS for Binary Tree Array
2分木配列に対するBreadth First Searchは簡単です。2分木配列の要素はレベルごとに置かれ、BFSもレベルごとに要素をチェックするので、BFSは単なる線形探索です
public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}深さ優先探索は少し難しくなっています。
スタックデータ構造を使用することで、古典的なバイナリツリーと同じように実装することができ、スタックにインデックスを置くだけです。
スタックや再帰を使わずにDFSを実装して、最終的には各ステップで正しいインデックスを選択するだけだとしたらどうでしょうか。
DFS for Binary Tree Array (without stack and recursion)
BFSと同様にルートインデックス 0 から開始します。
次に左の子を調べる必要がありますが、そのインデックスは式2*i+1で計算できます。
次の左の子に行く処理を2倍と呼ぶことにしましょう。
If next left child produce index out of array bounds exception we need to stop doubling and jump to the right child.
That’s a valid solution, but we can avoid unnesessary doubling.This observation is some height of the tree in elements is two times larger (and plus one) with height - 1.The reason that is the same way to the tree in the next child in the array bound.
height = 2の木は7個の要素、height = 3の木は7*2+1 = 15個の要素。
この観測結果を用いて、簡単な条件
i < array.length / 2この条件は木の葉以外のノードに対して有効であるか確認することができます。 しかし、この方法では左の子ノードしかチェックできない。
葉ノードで行き詰まり、2重化を適用できなくなったら、ジャンプ操作を行う。
このようなジャンプ操作は、単にリーフインデックスをインクリメントすることで実現できます。そのため、2重ジャンプを行う必要がある
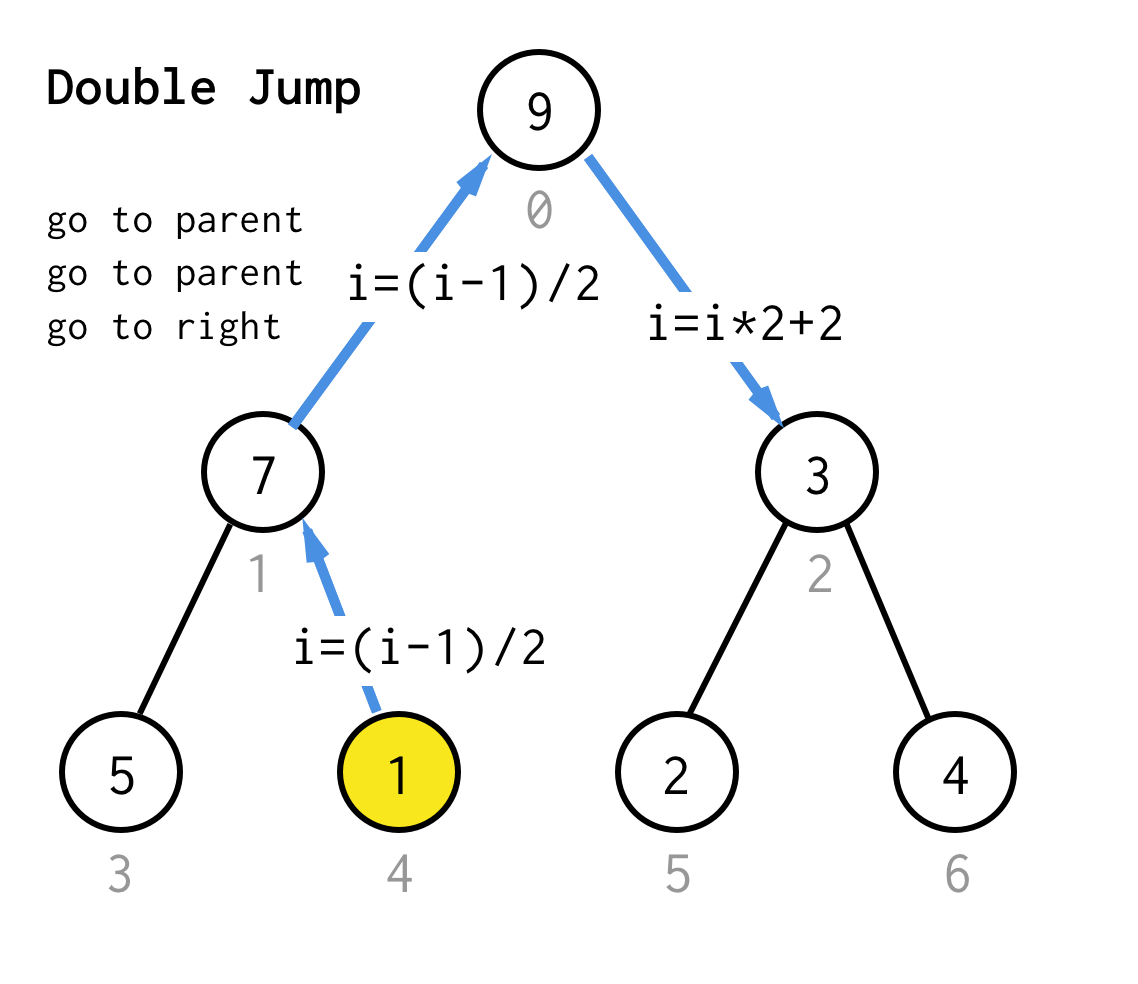
より汎用的にするために、我々のアルゴリズムでは、親へのジャンプをいくつ必要とするか指定し、常に正しい子へのジャンプで終了するジャンプN操作を定義できる。
高さ1の木では、1回のジャンプが必要で、ジャンプ1
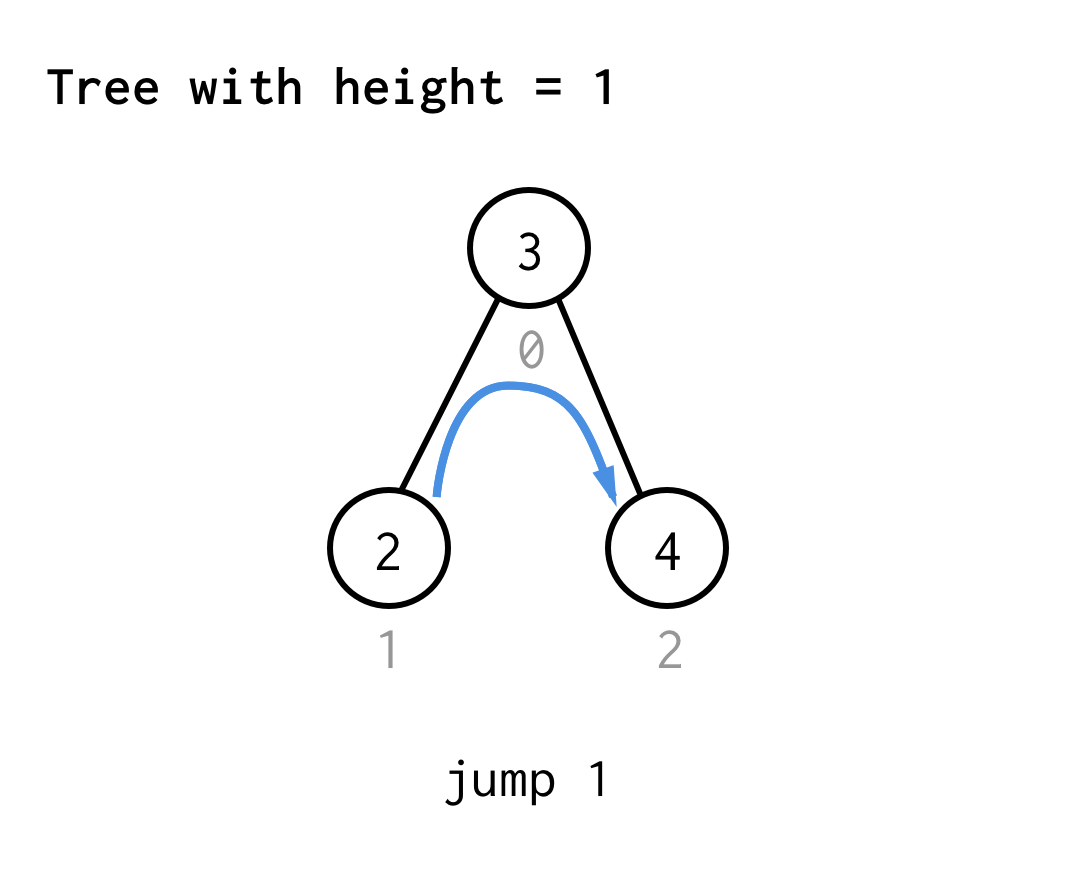
高さ2の木では、1回のジャンプ、2回のジャンプ、さらにもう1回のジャンプ
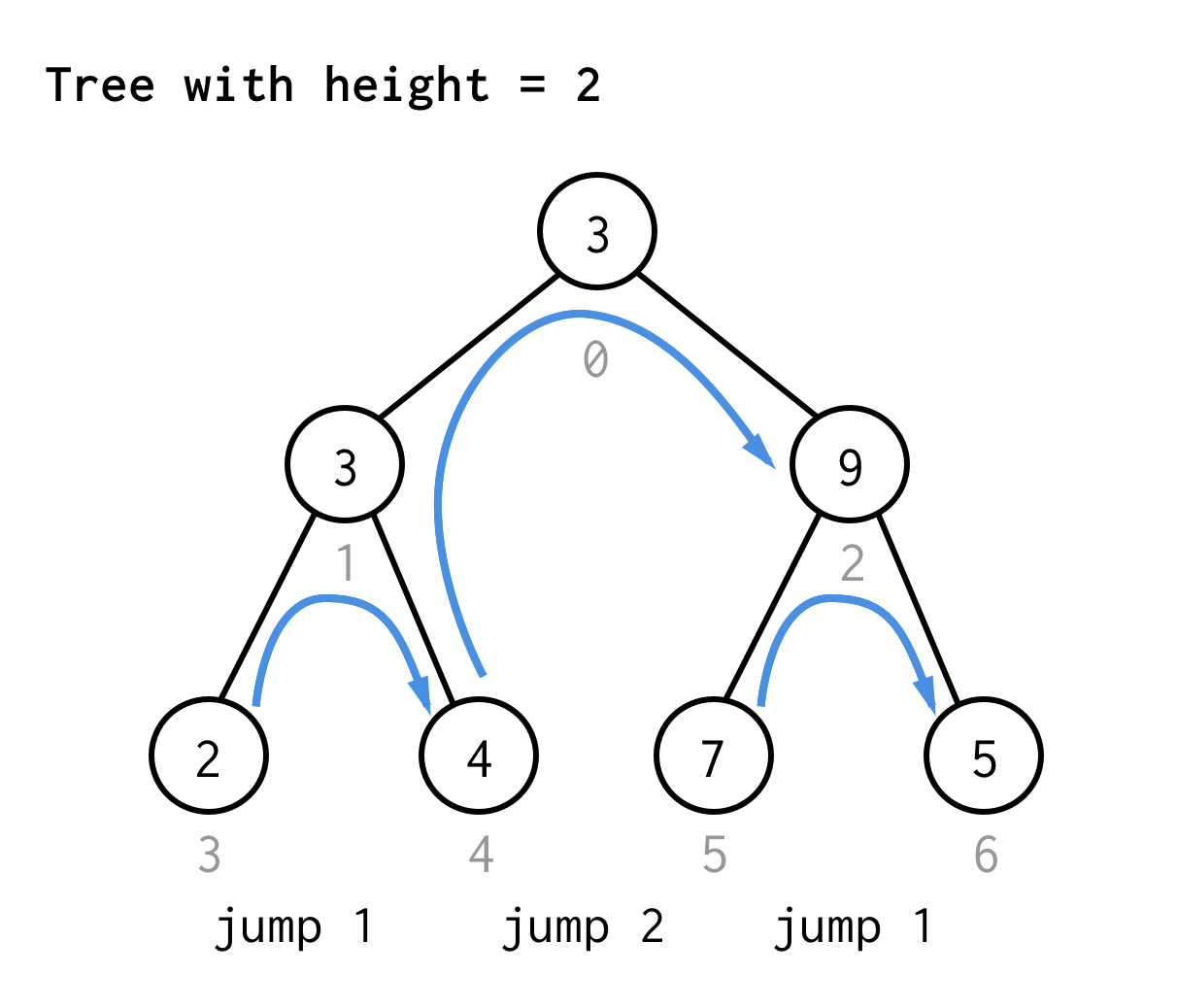
3では同じ規則を使って7回のジャンプが必要である。
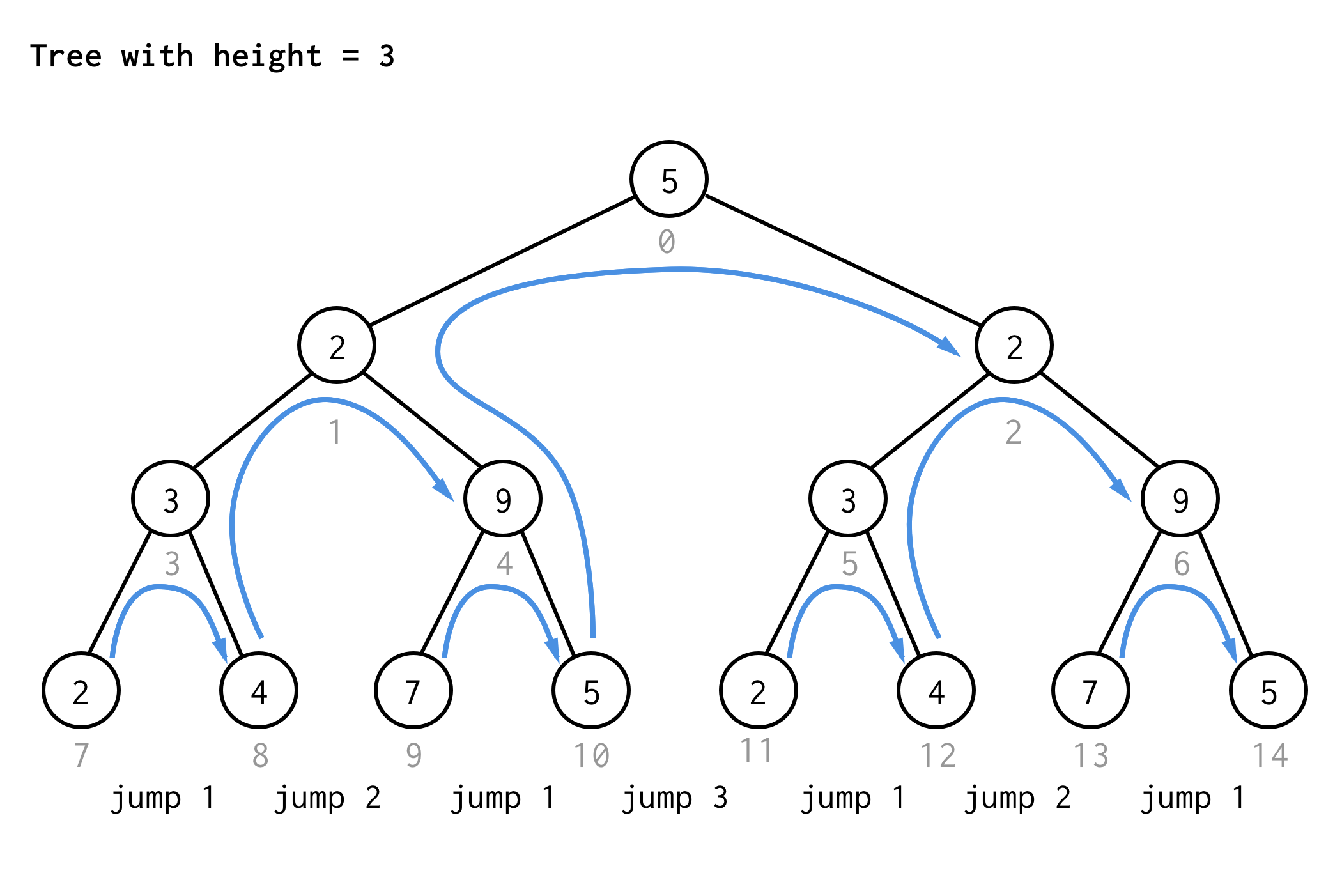
このパターンを見てください。
高さ4の木に同じルールを適用して、ジャンプの値だけを書き出すと、次のシーケンス番号が得られます
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
これはジミン語と呼ばれ、再帰的定義を持っていますが、再帰を使うことは許されないので、あまりよくはないでしょう。
ジャンプシーケンスをよく見ると、非再帰的なパターンがあることがわかります。
「3から始まるすべての8番目の要素」のような文を検証するには、j % 8 == 3をチェックし、それが本当なら親ノードへの3回のジャンプが必要です。
反復的なジャンプ処理は以下のようになります。
-
k = 1 - で開始し、
i = (i - 1)/2 - で親に1回ジャンプします。
leaf % 2*k == k - 1すべてのジャンプが成功したら終了 - さもなければ、
kに2*kと設定して繰り返しです。
今まで議論したことを全部まとめると
public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}完了です。 DFS for binary tree array without stack and recursion
Complexity
ループの中にループがあるので、2次関数的に見えますが、実際はどうなのか見てみましょう。
- 全体の半分のノード(
n/2)は2倍化戦略で、これは一定ですO(1) - 全体の残りの半分(
n/2)はリーフジャンプ戦略で、 - 半分のノード(
n/4)では親のジャンプ1回、繰り返し1回ですみます。O(1) - この半分から半分(
n/8)は2回のジャンプ、つまり2回の反復を必要とする。O(1) - …
- ルートへのフルジャンプが必要なリーフジャンプは
O(logN) - なので、
O(logN)を除くすべてのケースがO(1)であるとします。 ジャンプの平均はO(1) - 総複雑度は
O(n)
パフォーマンス
理論的には良いが、このアルゴリズムが実際にどう動くか、他と比較して見よう。
JMHを使って、5つのアルゴリズムをテストしています。
- BFS on Binary Tree (linked list as queue)
- BFS on Binary Tree Array (linear search)
- DFS on Binary Tree (stack)
- DFS (stack)
- BFS on Binary Tree (linear search) on Binary Tree Array (stack)
- Iterative DFS on Binary Tree Array
- アルゴリズム
- データ構造
- プログラミング
- BFS (linked list as queue)
あらかじめ木を作り、最後のノードにマッチするように述語を使っています。すべてのアルゴリズムで常に同じ数のノードをヒットするようにするため。
で、結果
Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s明らかに、配列上のBFSが勝ちますね。 ただの線形探索なので、2分木を配列で表現できるのであればそうすればいい。
記事で紹介したIterative DFSは、22位、4.5線形探索(配列上のBFS)より1倍遅い。
残りの3つはIterative DFSよりさらに遅く、おそらくデータ構造の追加、余分のスペースとメモリの割り当てがあるためだ。
Conclusion
Binary Tree Array は、階層的なデータ構造を静的配列(メモリ上の連続した領域)として表現する良いトリックである。 これは、古典的なバイナリ配列表現では不可能な、親から子への移動と子から親への移動のための単純なインデックス関係を定義する。 挿入/削除が遅いなどの欠点もありますが、2 進木配列のアプリケーションはたくさんあります。
これまで示したように、配列に実装した検索アルゴリズム、BFS、DFS は、参照ベースの構造上の他のアルゴリズムよりはるかに高速です。 実世界の問題では、それはそれほど重要ではなく、おそらく、私はまだ参照ベースのバイナリ配列を使用することになるでしょう。 次回の面接では「再帰とスタックを使わないバイナリ配列でのDFS」という質問を期待しています。
mishadoff 2017年09月10日
コメントを残す