Molecular Dipole Moments
複数の極性結合を含む分子では、分子双極子モーメントは個々の「結合双極子モーメント」とみなせるもののベクトルの組み合わせにすぎません。 数学的には、双極子モーメントはベクトルであり、大きさと方向の両方を持っています。 したがって、分子の双極子モーメントは、分子内の個々の結合の双極子モーメントのベクトル和となる。 個々の結合の双極子モーメントが互いに打ち消し合っていれば、正味の双極子モーメントは存在しない。 線状分子であるCO2がそうである(図(˶‾᷄ -̫ ‾᷅˵))。 CO2のC-O結合はそれぞれ極性をもっていますが、実験によるとCO2分子は双極子モーメントを持っていません。 CO2の2つのC-O結合の双極子の大きさは等しく、互いに180°の方向を向いているため、相殺されます。 その結果、CO2分子は電荷がかなり分離しているにもかかわらず、正味の双極子モーメントを持たない。 一方、H2O分子は直線状ではなく、3次元空間で曲がっているため、双極子モーメントが打ち消し合うことがない。 そのため、H2Oのような分子は正味の双極子モーメントを持っている。 このとき、電気陰性度の高い酸素に負の電荷が集中し、2つの水素に正の電荷が集中することが予想される。 この電荷の偏りによって、H2Oは他の水分子を含む他の偏った電荷を持つ種と水素結合することができる。
Figure \(\PageIndex{1}): How Individual Bond Dipole Moments Are Added Together to a Overall Molecular Dipole Moment for Two Triatomic Molecules with different Structures. (a) CO2では、C-O結合の双極子の大きさは等しいが、向きが180°反対である。 ベクトル和は0なので、CO2は正味の双極子を持ちません。 (b) H2Oでは、O-H結合の双極子の大きさは等しいが、互いに104.5°の向きになっている。 したがってベクトル和はゼロではなく、H2Oは正味の双極子モーメントを持つ。
以下は、二原子分子に存在する、あるいは分子内の結合双極子を考える場合の単純分離二電荷系の簡略化した式である。
この結合双極子µ (Greek mu)は、部分電荷(Q^+Θ)と(Q^-Θ)(またはより一般的な用語では、(δ^+)- \(δ^-Θ)) 間の距離 \(rΘ) にわたって分離した電荷による双極子と解釈し、その向きは結合軸に沿ったものである。 双極子モーメントの単位は通常デバイ(D)で、1デバイはSI単位で3.336×1030クーロンメートル(C-m)に相当する。 電子と陽子が一定の距離で離れている単純な系を考えてみよう。 電子の単位電荷は1.60 X 1019 C、陽子&電子は100 pm(典型的な共有結合の長さ程度)離れているので、双極子モーメントは次のように計算される:
Centa &= (1.60 \times 10^{-19}, C)(1.00 \times 10^{-10} \,m) \nonumber &= 1.60 \times 10^{-29} \end{align}]
&= 4.80
; D \end{align}
(4.80; Dǐ) は重要な参考値で、+1 と -1 の純電荷が 100 pm 離れていることを表しています。 しかし、電荷の分離を大きくすると、双極子モーメントが(直線的に)増加する:
- 陽子と電子が120 pm分離した場合。
- If the proton and electron were separated by 150 pm:
- If the proton and electron were separated by 200 pm:
Example \(\PageIndex{1}י): Water
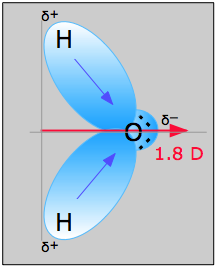
図中の水分子は、双極子モーメントの方向と大きさを決定することができます。 酸素と水素の電気陰性度から、その差は水素-酸素結合のそれぞれで1.2eである。 次に、酸素は電気陰性度が高いため、共有電子をより強く引っ張り、さらに2つの孤立電子を持つ。 このことから、双極子モーメントは2つの水素原子の間から酸素原子の方を向いていると結論づけることができる。 上の式を用いて、酸素原子と水素原子の距離に両者の電荷差を掛け、正味の双極子モーメントの方向を指すそれぞれの成分を求めると、双極子モーメントは1.85 Dとなる(分子の角度は104.5度)。5˚)。
O-H結合の結合モーメント=1.5Dなので、正味の双極子モーメントは
コメントを残す