固有ベクトル

Eigenvectors are special set of vectors associated with a linear system of equations (i.)…e., 782>

系の固有ベクトルおよび固有値を決定することは、物理学および工学において非常に重要であり、それは行列対角化と等価であり、安定性解析、回転体の物理、振動系の小振動など、いくつかの例を挙げるとよくある応用で発生するものである。 各固有ベクトルは、対応する固有値と呼ばれるものと対になっている。 数学的には、固有ベクトルを左固有ベクトルと右固有ベクトルの2種類に区別する必要がある。 しかし、物理学や工学の多くの問題では、右固有ベクトルのみを考慮すれば十分です。 782>

正方行列を固有値と固有ベクトルに分解することをこの作業では固有分解と呼び、の固有ベクトルからなる行列が正方である限り常にこの分解が可能であることを固有分解定理と呼んでいる。

右固有ベクトルを

(1)

ここには行列と定義される。 ということは

(2)

つまり右の固有値はゼロ行列式を持たねばならない、即ち。e.,

(3)

同様に、左固有ベクトルを

と定義します。 “>

(4)

各辺の転置を取ると

(5)

これは

(6)

もう一度整理すると、

(7)

つまり

(8)

書き換えると

＜8254>

		(9)
			(10)
			(11)

ここで最後のステップは恒等式

(12)

任意のとに対して共に0になる式（◇）と（11）を等化するには、したがって、即ち。

ここで、を右固有ベクトルの列で形成される行列とし、を左固有ベクトルの行で形成される行列とすると、左と右固有値は同等である。

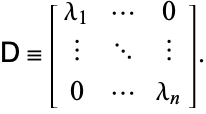(13)

次に

とすると

			(14)
			(15)

and

			(16)
			(17)

ソ

(18)

しかしこの式は

という形になっているのです。

(19)

ここで、は対角行列である。 ということは、も対角であることが真である。 特にが対称行列であれば、左右の固有ベクトルは単に互いの転置であり、が自己共役行列（すなわちエルミート）であれば、左右の固有ベクトルは共役行列となる。

固有ベクトルはゼロベクトルと等しくないことがある。 固有ベクトルの0でないスカラー倍は元の固有ベクトルと等価である。 したがって、一般性を損なうことなく、固有ベクトルはしばしば単位長に正規化されます。

行列は常に 固有値を持ち、その一部または全部は縮退しているかもしれませんが、そのような行列は 0 から 線形独立固有ベクトルを持つかもしれません。 例えば、行列は単一の固有ベクトルのみを持ちます。

固有ベクトルはWolfram LanguageでEigenvectorsを使って計算することができます。 このコマンドは常に長さのリストを返すので，線形独立でない固有ベクトルはすべて0ベクトルとして返されます． 固有ベクトルと固有値はEigensystemというコマンドで一緒に返すことができます．

固有ベクトル, , と対応する固有値 を持つ 行列 が与えられたとき、次のようになる。 , とすると、任意のベクトル は

(20)

行列を適用する。

)

			(21)
			(22)

so

(23)

もし、そしてであるから、

(24)

従って、任意のベクトルに行列を繰り返し驚くほど適用すると、最大固有値を持つ固有ベクトルに比例したベクトルになります。