三角形の角の性質

関連項目：
その他の幾何学のレッスン
幾何学のワークシート
幾何学のゲーム
これらのレッスンでは、三角形の角の性質についてまとめて説明します。

• 三角形の和の定理 – 三角形の3つの角の和は常に180°
• 内角とその隣の外角の和は180°
• 外角の定理 – 三角形の外角は2つの反対側の内角の和に等しい
• 等角三角には60°ずつの3等角が存在します。 二等辺三角形は2つの等しい辺に対向する角がある

三角形の角は次のような性質を持っている。

性質1：三角形の和の定理

三角形の3つの角の和は常に180°である

例:

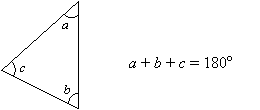
三角形の和の定理の証明方法
次のビデオでは、三角形の角の和が180度であることを証明する方法を紹介します。 (三角形の和の定理)

• Show Step-by-step Solutions

How to Find the Missing Angle in a Triangle using the Triangle Sum Theorem?
Step 1: すべての角を足して180°になるように方程式を書き出す。
ステップ2：xを解きます。
ステップ3：足りない角度を求めて代入します。

• ステップごとの解答を表示する

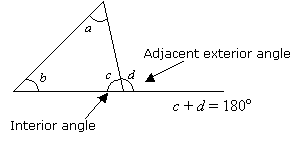
物件2：

内角とその隣の外角との和は180°である。

例:

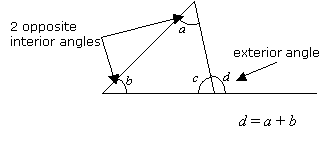
性質3：外角の定理

三角形の外角は2つの対向する内角の和に等しくなる。

例題．

三角形の外角
三角形の未知の角度を求める
例題：
1. a＝40°、b＝60°の三角形abcを評価する。 ∠acbの外角は何度だろうか。
2.a＝50°、b＝30°の三角形abcを求めよ。 ∠acbの外角は？
2. a = 90°、b = 40°の三角形abcを評価する。 ∠acbに対する外角は何度ですか？

• Show Step-by-step Solutions

三角形の角度を含む問題を解くために外角の定理を使うには？

• Show Step-by-step Solutions

性質4：

正三角形の3等角は各60°である。
二等辺三角形には2つの等しい角があり、それは2つの等しい辺に対向する角である。
二等辺三角形で足りない角度を見つけるには？

• 段階的な解答を表示

平行線と三角形の角の和の定理

• 段階的な解答を表示

上記の角の性質は三角形の未知の角度を見つけるのに役に立ちます。

例題：次の三角形でxの値を求めよ。

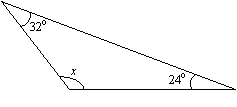
解答。

x + 24° + 32° = 180° (角の和は180°)
x + 56° = 180°
x = 180° – 56° = 124°

例題:

次の三角形におけるxとyの値を求めよ。

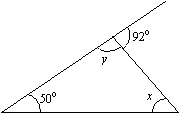
解答。

x + 50° = 92°（反対側の内角の和＝外角）
x = 92° – 50° = 42°

y + 92° = 180°（内角＋隣接する外角＝180°）
y = 180° – 92° = 88°

以下の無料のマスウェイ計算と問題解決ツールでいろいろと計算練習をしてみてください。 与えられた例を試すか、独自の問題を入力し、ステップバイステップの説明であなたの答えを確認してください。