ゼロで割る秘密の魔法

ゼロで割ってはいけない。 私たちは皆、学校でこのことを教えられましたし、ほとんどの日常的な場面で、これは良いアドバイスです。 ゼロで割っても意味がないことはほとんどありませんし、Siri にゼロで割ってくれと頼むと、あなたには友達がいないと言われるでしょう。

しかし、なぜゼロで割ることがそんなに悪いことなのでしょうか？ また、ゼロで割ることが良いことになるケースはあるのでしょうか。 もしあなたが高校時代に注意を払わなかったのなら、簡単に復習することで、数学の多くの不思議のうちの1つに目を向けることができます。

算数では、ゼロで割ることはゼロをかけることとも解釈できるので、ゼロで割ることは意味がないのです。 3/0=Xは0*X=3と同じ式になる。 明らかに、その方程式を成り立たせるために X に差し込める数字はありません。

ゼロをそれ自体で割ろうとすると、同じような状況が生じます。 0/0=X は 0*X=0 と書き直せますが、ここでの問題は、あらゆる数字が機能することです。 Xは何でもよいので、この式はあまり役に立ちません。

しかし、ゼロで割ることが実際に機能し、実際、問題を解くために不可欠であるケースもあります。 これは、ニュートンが微積分を発明したときの洞察でした。

たとえば、ある曲線があって、特定の点での下の曲線の傾きを求めようとしているとします。 これは、接線と呼ばれる、その点でのみ曲線に接する直線の傾きを求めようとするのと同じことです。 多くの場合、代数学だけではその傾きを求めることはできません。

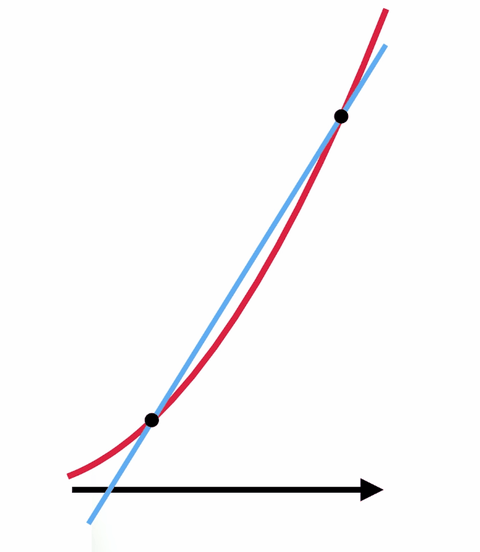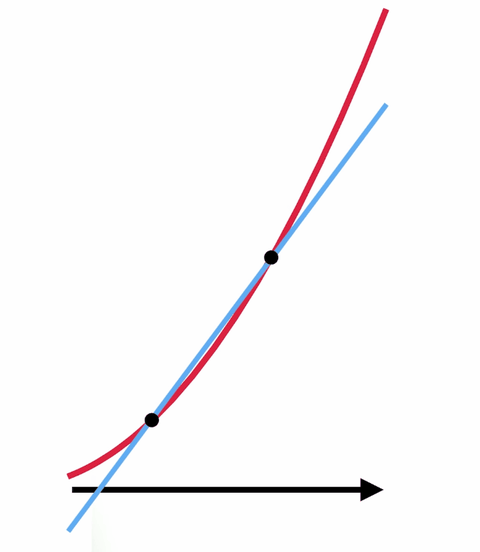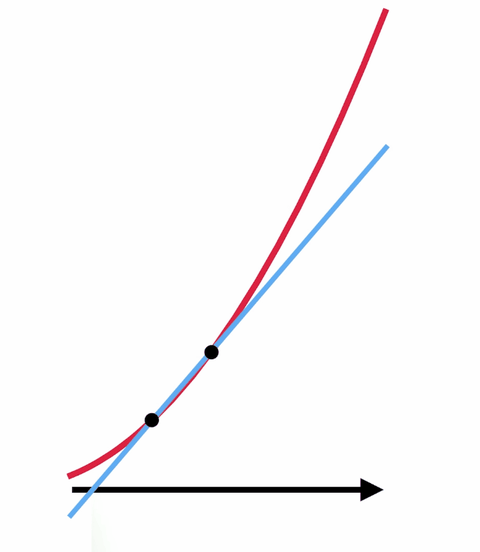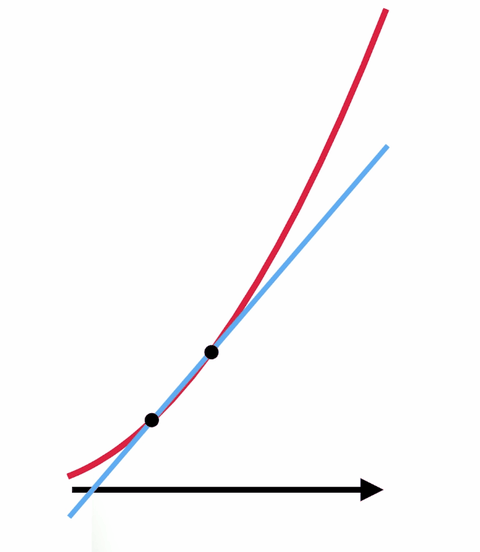
しかし、微積分とゼロで割るマジックを使ったトリックがあります。 接線を求める代わりに、曲線に2点で接する直線の傾きを求める方がずっと簡単です。 その2点をどんどん近づけていけば、望んだ線に近い線が得られる。

2つの点を互いに重なるように、つまり実質的に1つしかないように移動すれば、望んだ元の接線が得られますが、今度は傾きを求めることができます。

ゼロで割るトリックは、本質的にいくつかの余分なコンテキストを作成することです。 0/0 の最初の問題は、すべての数が答えになる可能性があることです。したがって、いくつかの制限要因を導入することで、可能な答えを絞り込むことができます。 ゼロや無限大、あらゆる種類の不可能な方程式で遊ぶことが当たり前になる。 ゼロで割れるようになると、数学はもう二度と同じものではなくなります。