X

プライバシー & Cookies

このサイトではクッキーを使用しています。 続行することで、その使用に同意したことになります。 Cookieを制御する方法など、詳しくはこちら

Got It！

広告

スパイラルとは「ある点から発し、その点を中心に回転しながら遠くへ向かう」曲線です。 このブログでは2次元の螺旋について説明します（3次元の螺旋もいろいろあるので注意してください）。

アルキメデス螺旋

この螺旋は有名なギリシャの数学者アルキメデスから名付けられたもので、彼が著書『On Spirals』で最初に記述したものです。 これは次の極方程式で記述される:

\, r=a+b\theta

ここでaとbは実数。

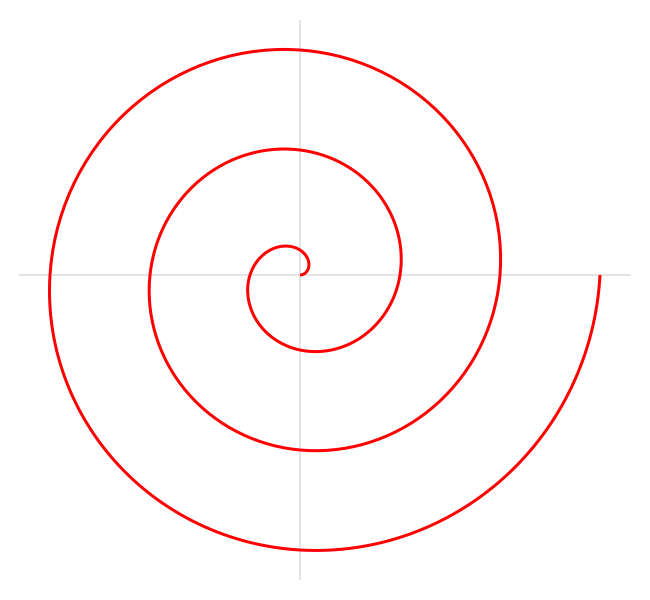
パラメータaを変えることにより螺旋は曲がり、パラメータbは連続した回転間の距離を制御する。

Fermat’s Spiral

Fermatの螺旋は次の極方程式に従う放物線螺旋である：

r=pm \theta ^{1/2},

アルキメデス螺旋の一種である。

オイラー螺旋

コルヌ螺旋とも呼ばれ、原点からの距離が大きくなると曲率が大きくなる曲線で、「円曲線の曲率は半径の逆数に等しい」と言われています。

パラメータ形式はフレネルの間隔を持つ2つの方程式からなり、近似的にしか解けない。

S(x)=int_0^x \sin(t^2)\,\mathrm{d}t,\quad C(x)=int_0^x \cos(t^2)\,\mathrm{d}t.

これらの積分、ひいてはオイラー螺旋は、波動論におけるフレネルの1スリットでの回折のエネルギー分布を記述するのに使える。

ハイパーボリック螺旋

1704年にピエール・バリニヨンが初めて考え出した、超越曲線で「多項式を満たさない解析関数」という意味である。 アルキメデスの螺旋の逆で、次の極方程式を持つ:

r={frac {a}{theta }}

中心では極から無限距離にあり、0から始まるθに対して、rは無限大から始まる。

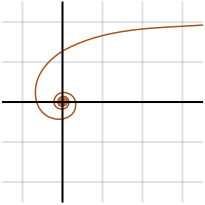
リトゥース

リトゥースは極方程式:

r^2theta = k \,

ここでkは定数である螺旋である。 したがって、角度は半径の2乗に反比例する。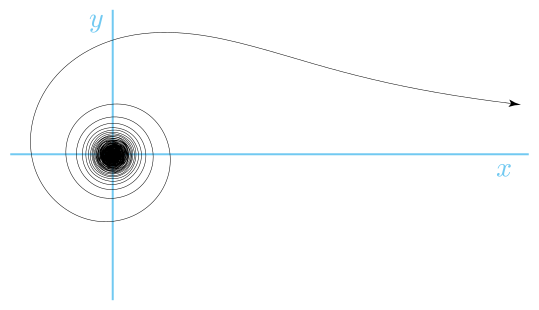

この曲線は1722年に発表された論文集でRoger Cotesによって古代ローマのLituus（曲がったオーギュラス・スタッフまたはウォー・トランペット）にちなんで名付けられた。

対数螺旋

自然界にもしばしば見られる自己相似螺旋である。 デカルトによって初めて記述されたが、ヤコブ・ベルヌーイによって深く研究され、”驚異の螺旋 “と呼ばれるようになった。 極方程式は

である。