Eigenvector

Eigenvectoren zijn een speciale verzameling vectoren die geassocieerd zijn met een lineair stelsel van vergelijkingen (d.w.z.e., een matrixvergelijking) die soms ook karakteristieke vectoren, eigenvectoren of latente vectoren worden genoemd (Marcus and Minc 1988, p. 144).

De bepaling van de eigenvectoren en eigenwaarden van een stelsel is uiterst belangrijk in de natuurkunde en techniek, waar het equivalent is aan matrixdiagonalisering en voorkomt in veelvoorkomende toepassingen zoals stabiliteitsanalyse, de fysica van roterende lichamen, en kleine oscillaties van trillende systemen, om er maar een paar te noemen. Elke eigenvector wordt gekoppeld aan een overeenkomstige zogenaamde eigenwaarde. Wiskundig gezien moeten twee verschillende soorten eigenvectoren worden onderscheiden: linker eigenvectoren en rechter eigenvectoren. Voor veel problemen in de natuurkunde en techniek is het echter voldoende alleen de rechter eigenvectoren te beschouwen. De term “eigenvector” die in dergelijke toepassingen zonder kwalificatie wordt gebruikt, kan daarom worden opgevat als een rechter eigenvector.

De ontbinding van een vierkante matrix in eigenwaarden en eigenvectoren staat in dit werk bekend als eigendecompositie, en het feit dat deze ontbinding altijd mogelijk is zolang de matrix bestaande uit de eigenvectoren van vierkant is, staat bekend als de eigendecompositietheorema.

Definieer een rechter eigenvector als een kolomvector die voldoet

(1)

waar een matrix is, dus

(2)

wat betekent dat de juiste eigenwaarden een determinant van nul moeten hebben, d.w.z.e.,

(3)

Op soortgelijke wijze definieert men een linker eigenvector als een rijvector die voldoet aan

(4)

De transpositie van elke zijde nemen geeft

(5)

die kan worden herschreven als

(6)

Herschik opnieuw om

(7)

wat betekent

(8)

Herschrijven geeft

			(9)
			(10)
			(11)

waarbij de laatste stap volgt uit de identiteit

(12)

Equivalente vergelijkingen (◇) en (11), die beide gelijk zijn aan 0 voor willekeurige en , vereisen daarom dat , d.w.z., linker en rechter eigenwaarde equivalent zijn, een bewering die niet waar is voor eigenvectoren.

Laat een matrix zijn gevormd door de kolommen van de rechter eigenvectoren en een matrix gevormd door de rijen van de linker eigenvectoren. Zij

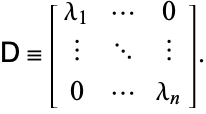(13)

Toen

			(14)
			(15)

en

			(16)
			(17)

zo

(18)

Maar deze vergelijking is van de vorm

(19)

waar een diagonaalmatrix is, dus moet het waar zijn dat ook diagonaal is. In het bijzonder, als een symmetrische matrix is, dan zijn de linker en rechter eigenvectoren eenvoudigweg elkaars transponering, en als een self-adjoint matrix is (d.w.z. Hermitiaans), dan zijn de linker en rechter eigenvectoren adjunct matrices.

Eigenvectoren mogen niet gelijk zijn aan de nulvector. Een niet nul scalair veelvoud van een eigenvector is gelijkwaardig aan de oorspronkelijke eigenvector. Vandaar dat, zonder verlies van algemeenheid, eigenvectoren vaak genormaliseerd worden tot eenheidslengte.

Een matrix heeft altijd eigenwaarden, waarvan sommige of alle ontaard kunnen zijn, maar zo’n matrix kan tussen 0 en lineair onafhankelijke eigenvectoren hebben. Bijvoorbeeld, de matrix heeft slechts de enkele eigenvector .

Eigenvectoren kunnen in de Wolfram Language berekend worden met Eigenvectoren. Dit commando geeft altijd een lijst van lengte terug, dus alle eigenvectoren die niet lineair onafhankelijk zijn worden als nulvectoren teruggegeven. Eigenvectoren en eigenwaarden kunnen samen teruggegeven worden met het commando Eigensysteem.

Gegeven een matrix met eigenvectoren , , en en bijbehorende eigenwaarden , , en , dan kan een willekeurige vector geschreven worden

(20)

Toepassing van de matrix ,

			(21)
			(22)

zo

(23)

Als , en , dan volgt daaruit

(24)

dus herhaalde toepassing van de matrix op een willekeurige vector levert verbazingwekkend genoeg een vector op die evenredig is aan de eigenvector met de grootste eigenwaarde.