Die Synchrondrehzahl ist die Drehzahl der Umdrehung des Magnetfeldes in der Statorwicklung des Motors. Sie ist die Drehzahl, bei der die elektromotorische Kraft von der Wechselmaschine erzeugt wird. Die Synchrondrehzahl ergibt sich aus der nachstehenden Beziehung.

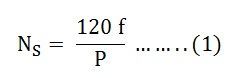
synchronous-speed-eq1

Die obige Gleichung (1) zeigt, dass die Rotordrehzahl N in einem konstanten Verhältnis zu den Feldpolen und der Frequenz der erzeugten Spannung in der Ankerwicklung steht. Eine Maschine, die mit Synchrondrehzahl läuft, wird als Synchronmaschine bezeichnet. Eine Wechselstrommaschine, bei der sich der Rotor mit einer Geschwindigkeit bewegt und ein konstantes Verhältnis zwischen der Frequenz der Spannung in der Ankerwicklung und der Anzahl der Pole herstellt, heißt also Synchronmaschine.

Die nachstehende Tabelle gibt die Anzahl der Pole und die Synchrondrehzahlen für eine Netzfrequenz von 50 Hertz an.

Anzahl der Pole Synchrondrehzahl NS in r.p.m
2 3000
4 1500
6 1000
8 750
10 600
12 500

Zusammenhang zwischen Drehzahl und Frequenz

Die Frequenz der erzeugten Spannung hängt von der Anzahl der Feldpole und von der Drehzahl ab, mit der die Feldpole gedreht werden. Eine vollständige Periode der Spannung wird in einer Ankerspule erzeugt, wenn ein Paar Feldpole über die Spule läuft.

Lassen Sie,

  • P die Gesamtzahl der Feldpole sein,
  • p ist das Paar der Feldpole,
  • N ist die Geschwindigkeit des Feldes in Umdrehungen pro Minute (r.p.m),
  • n ist die Anzahl der Feldpole in Umdrehungen pro Sekunde (r.p.s), und
  • f ist die Frequenz der erzeugten Spannung in Hertz.

Wie wir wissen,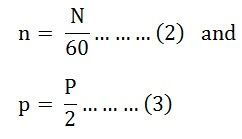synchronous-speed-eq2

wird eine Ankerspule bei einer Umdrehung des Rotors von P/2 Nordpolen und P/2 Südpolen geschnitten. Da ein Zyklus in einer Ankerspule erzeugt wird, wenn ein Paar Feldpole über die Spule läuft. Die Anzahl der Zyklen, die durch eine Umdrehung des Rotors erzeugt werden. ist gleich der Anzahl der Polpaare, d.h.,

  • Anzahl der Zyklen pro Umdrehung = p
  • Anzahl der Umdrehungen pro Sekunde = n

Nun ist die Frequenz,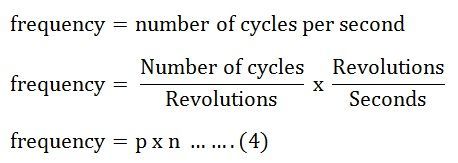synchronous-speed-eq3

Setzt man die Werte von n und p aus den Gleichungen (2) und (3) in Gleichung (4) ein, so erhält man

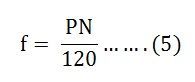
synchronous-speed-eq4

Die obige Gleichung (3) und (5) ergibt die Beziehung zwischen der Anzahl der Pole, der Geschwindigkeit und der Frequenz.