Datenschutz & Cookies
Diese Seite verwendet Cookies. Wenn Sie fortfahren, erklären Sie sich mit deren Verwendung einverstanden. Erfahren Sie mehr, auch wie Sie Cookies kontrollieren können.
Eine Spirale ist eine Kurve, die „von einem Punkt ausgeht und sich weiter entfernt, während sie um den Punkt kreist“.

Es gibt viele verschiedene Arten von Spiralen, abhängig von den Formeln, die sie erzeugen. In diesem Blog-Beitrag werde ich zweidimensionale Spiralen besprechen (beachte, dass es auch eine Vielzahl von dreidimensionalen Spiralen gibt).
Archimedische Spirale
Dies ist eine Spirale, die nach dem berühmten griechischen Mathematiker Archimedes benannt ist, der sie als erster in seinem Buch „Über Spiralen“ beschrieben hat. Sie wird durch die folgende polare Gleichung beschrieben:
wobei a und b reelle Zahlen sind.
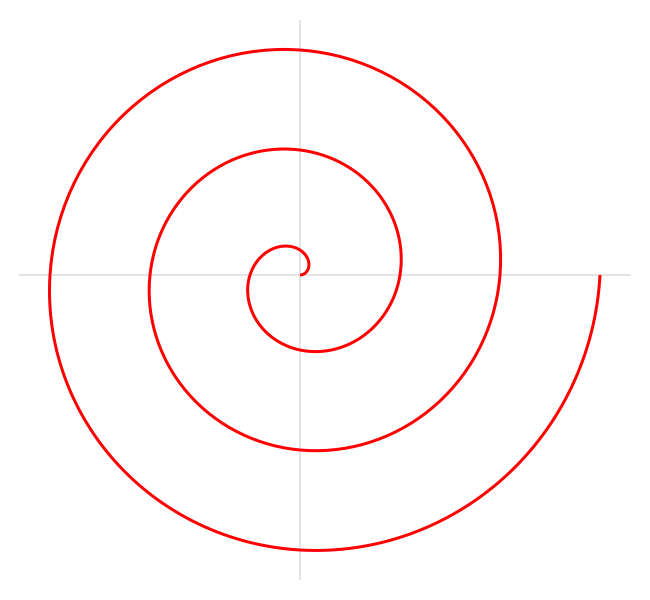
Indem man den Parameter a ändert, dreht sich die Spirale, und der Parameter b steuert den Abstand zwischen aufeinander folgenden Drehungen.
Fermatsche Spirale
Die Fermatsche Spirale ist eine parabolische Spirale, die der folgenden polaren Gleichung gehorcht:
Sie ist ein Typ der archimedischen Spirale.

Euler-Spirale
Auch bekannt als Cornu-Spirale, ist sie eine Kurve, deren Krümmung mit zunehmendem Abstand vom Ursprung wächst; „die Krümmung einer Kreiskurve ist gleich dem Kehrwert des Radius“.

Die Parameterform besteht aus zwei Gleichungen mit Fresnelschen Intervallen, die nur näherungsweise gelöst werden können.
Diese Integrale und damit die Eulersche Spirale können verwendet werden, um die Energieverteilung der Fresnelschen Beugung an einem Einzelspalt in der Wellentheorie zu beschreiben.
Hyperbolische Spirale
Die hyperbolische Spirale wurde erstmals 1704 von Pierre Varignon erdacht und ist eine transzendentale Kurve, was bedeutet, dass „sie eine analytische Funktion ist, die keine Polynomgleichung erfüllt“. Sie ist das Gegenteil einer archimedischen Spirale und hat daher folgende Polgleichung:
Im Zentrum befindet sie sich in unendlicher Entfernung vom Pol; für θ, das bei 0 beginnt, beginnt r bei unendlich.
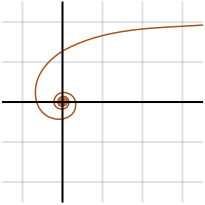
Lituus
Der Lituus ist eine Spirale mit einer polaren Gleichung:
wobei k eine Konstante ist. Der Winkel ist also umgekehrt proportional zum Quadrat des Radius. 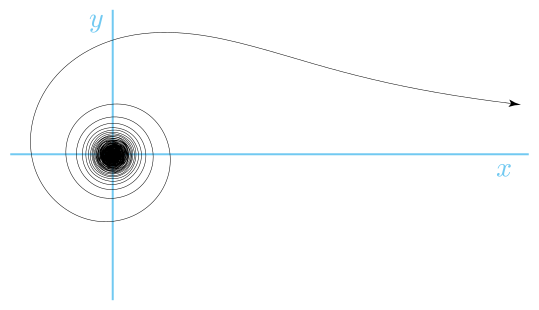
Die Kurve wurde von Roger Cotes in einer 1722 veröffentlichten Sammlung von Abhandlungen nach dem antiken römischen lituus (einem gebogenen Augurenstab oder Kriegstrompete) benannt.
Logarithmische Spirale
 Die logarithmische Spirale ist eine selbstähnliche Spirale, die häufig in der Natur auftritt. Sie wurde erstmals von Descartes beschrieben, aber von Jacob Bernoulli, der sie „die wunderbare Spirale“ nannte, eingehend untersucht. Sie hat eine polare Gleichung von
Die logarithmische Spirale ist eine selbstähnliche Spirale, die häufig in der Natur auftritt. Sie wurde erstmals von Descartes beschrieben, aber von Jacob Bernoulli, der sie „die wunderbare Spirale“ nannte, eingehend untersucht. Sie hat eine polare Gleichung von





Schreibe einen Kommentar