mishadoff thoughts

Implementing Depth-First Search for the Binary Tree without stack and recursion.

Binary Tree Array

Dies ist ein binärer Baum.

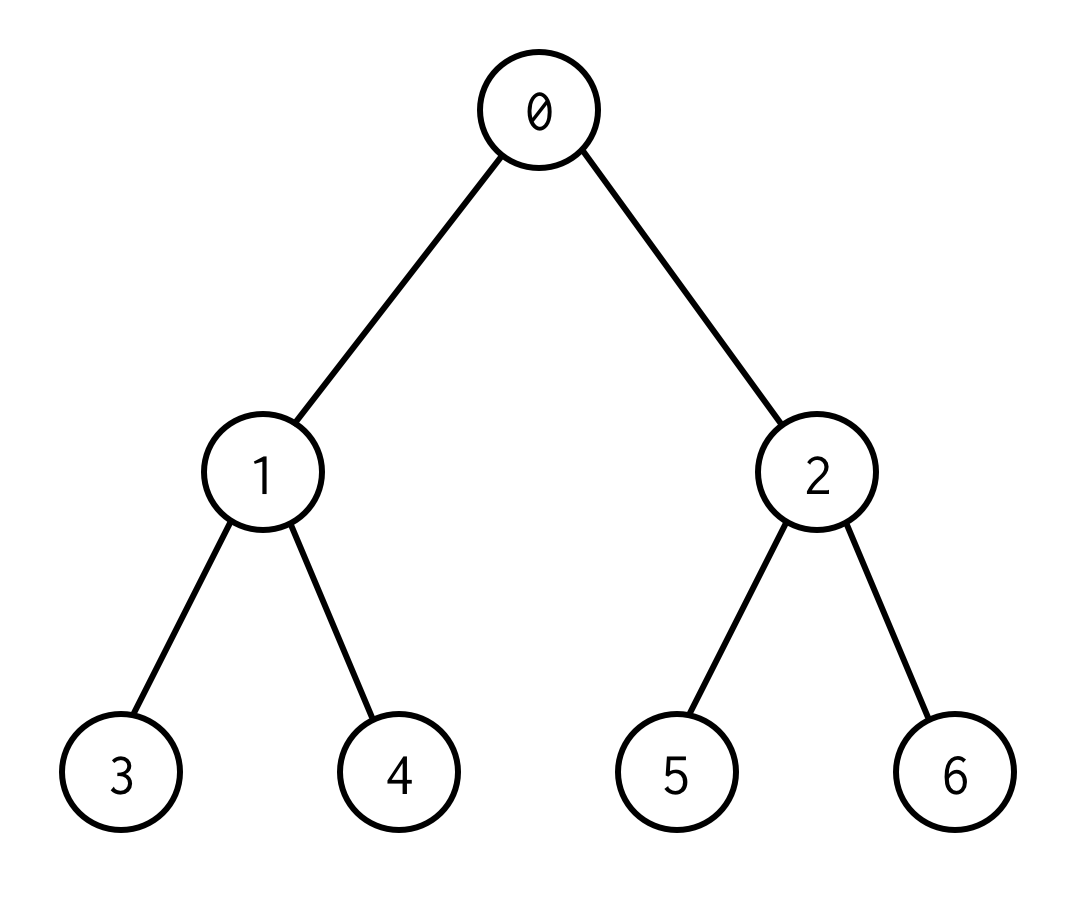
0ist ein Wurzelknoten.
0hat zwei Kinder: links 1 und rechts: 2.
Jedes seiner Kinder hat seine Kinder usw.
Die Knoten ohne Kinder sind Blattknoten (3,4,5,6).

Die Anzahl der Kanten zwischen Wurzel- und Blattknoten definieren die Baumhöhe.2Der Baum oben hat die Höhe 2.

Standardansatz zur Implementierung eines Binärbaums ist die Definition einer Klasse namens BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Es gibt jedoch einen Trick, um einen Binärbaum nur mit statischen Arrays zu implementieren.Wenn man alle Knoten im Binärbaum nach Ebenen aufzählt, beginnend bei Null, kann man sie in ein Array packen.

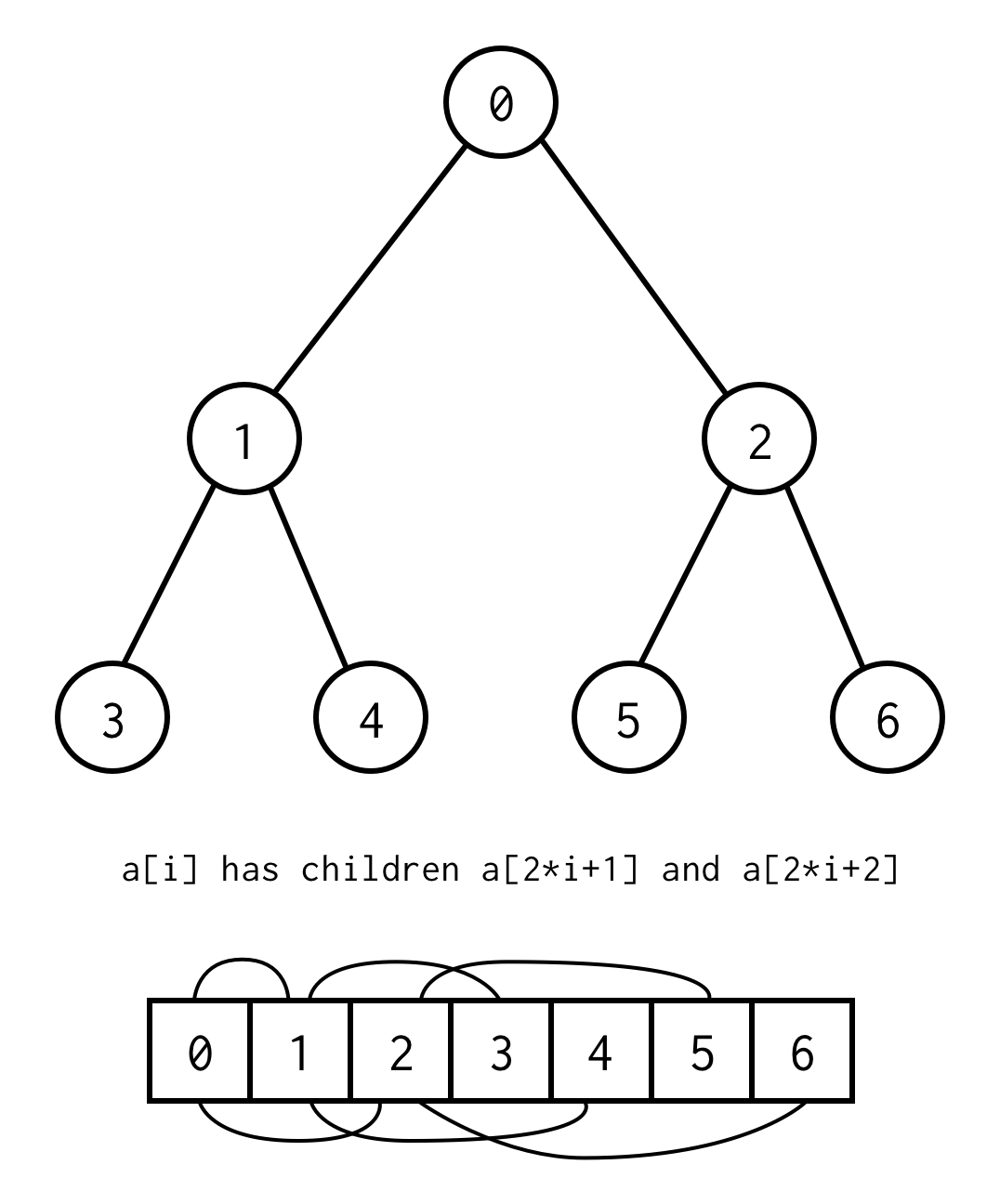
Die Beziehung zwischen dem Elternindex und dem Kindindex erlaubt es uns, sowohl vom Elternteil zum Kind als auch vom Kind zum Elternteil zu gehen

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Wichtig ist, dass der Baum vollständig sein sollte, was bedeutet, dass er für eine bestimmte Höhe genau Elemente enthalten sollte.

Sie können diese Anforderung umgehen, indem Sie null anstelle der fehlenden Elemente setzen, wobei die Aufzählung auch für leere Knoten gilt. Dies sollte jeden möglichen Binärbaum abdecken.

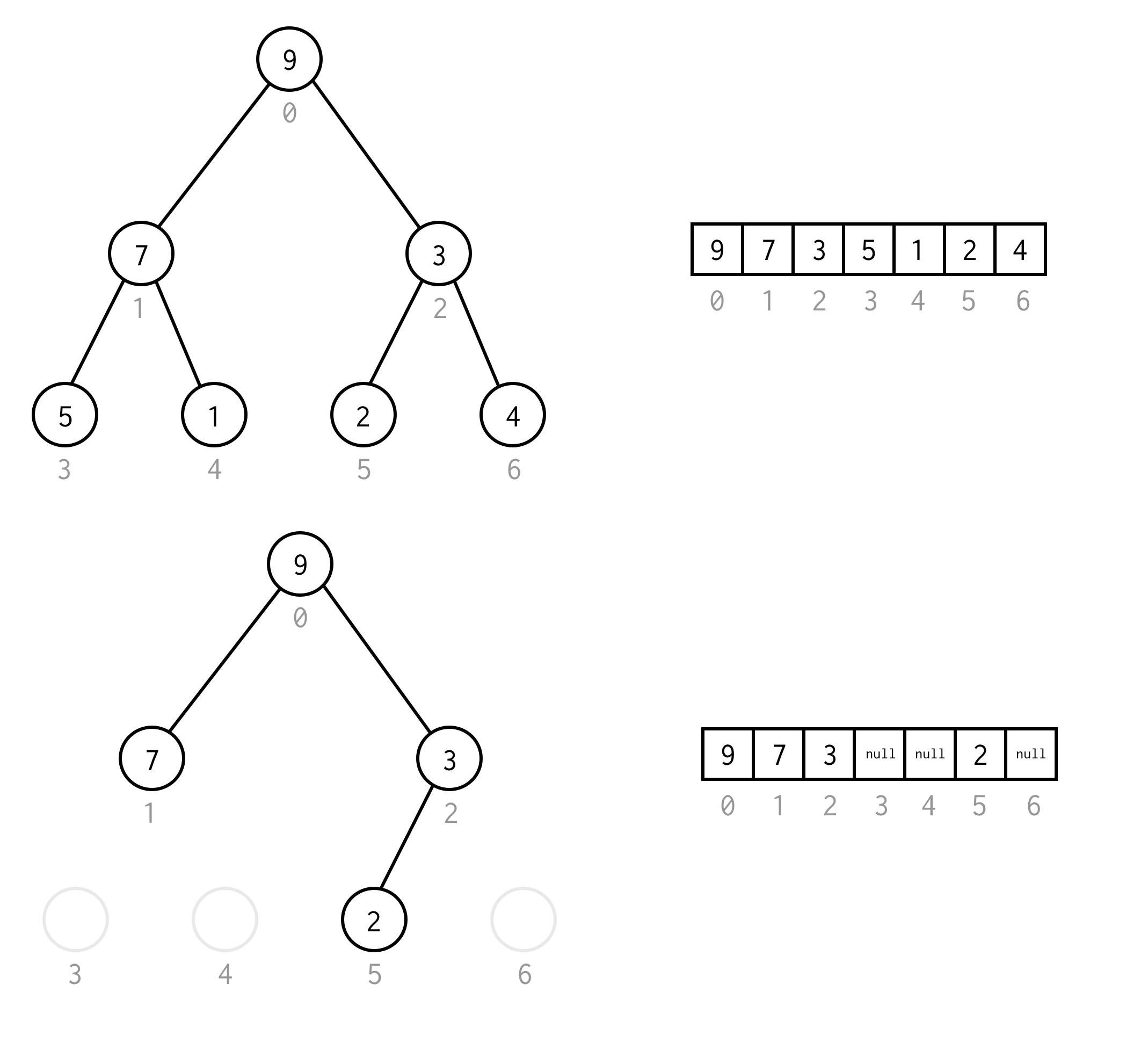
Eine solche Array-Darstellung für einen Binärbaum nennen wir Binärbaum-Array.Wir nehmen immer an, dass es Elemente enthält.

BFS vs DFS

Es gibt zwei Suchalgorithmen für Binärbäume:Breadth-First-Search (BFS) und Depth-First-Search (DFS).

Der beste Weg, sie zu verstehen, ist visuell

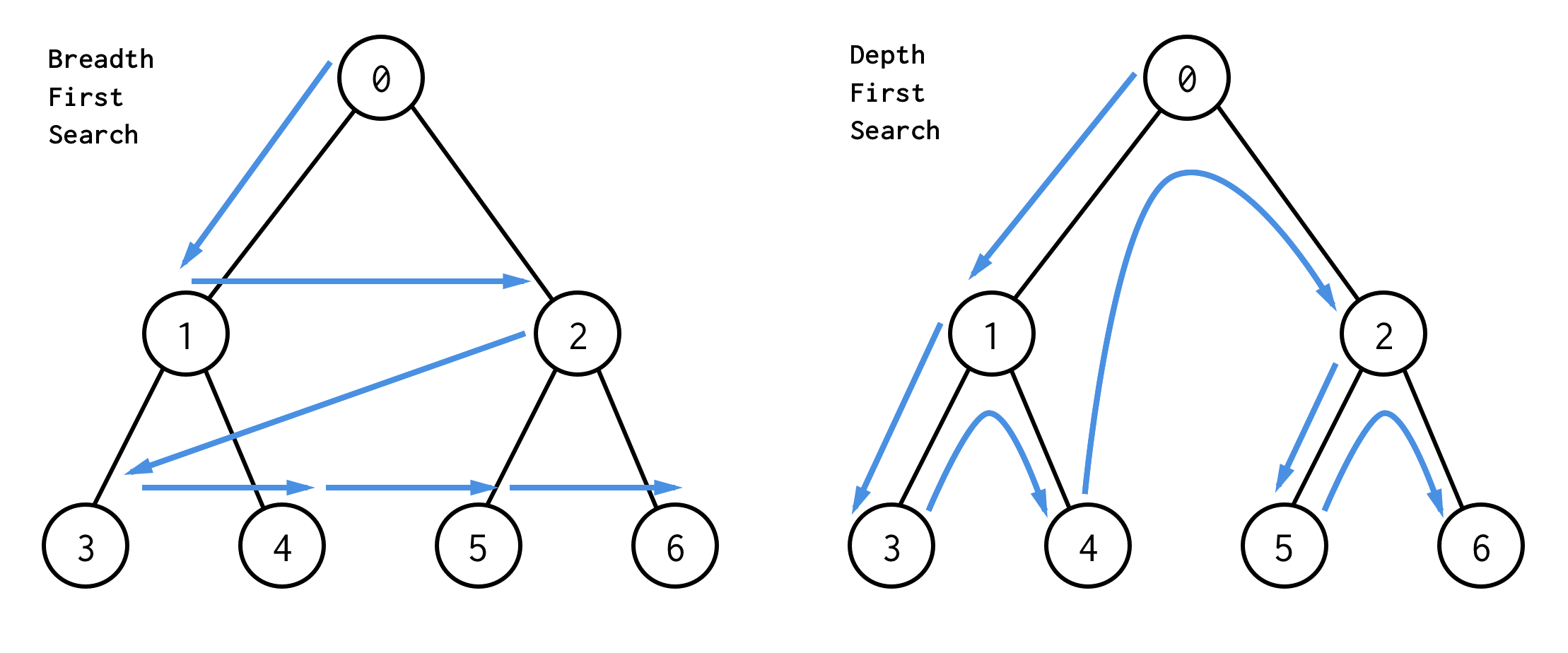
BFS sucht Knoten Ebene für Ebene, beginnend mit dem Wurzelknoten. Dann werden seine Kinder überprüft. Dann Kinder für Kinder und so weiter, bis alle Knoten abgearbeitet sind oder ein Knoten gefunden wurde, der die Suchbedingung erfüllt.

DFS verhält sich anders. Es prüft alle Knoten von ganz links von der Wurzel bis zum Blatt, dann springt es nach oben und prüft den rechten Knoten usw.

Für klassische Binärbäume wird BFS mit der Datenstruktur Queue implementiert (LinkedList implementiert Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Wenn man Queue durch Stack ersetzt, erhält man DFS-Implementierung.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Angenommen, Sie müssen im folgenden Baum einen Knoten mit dem Wert 1 finden.

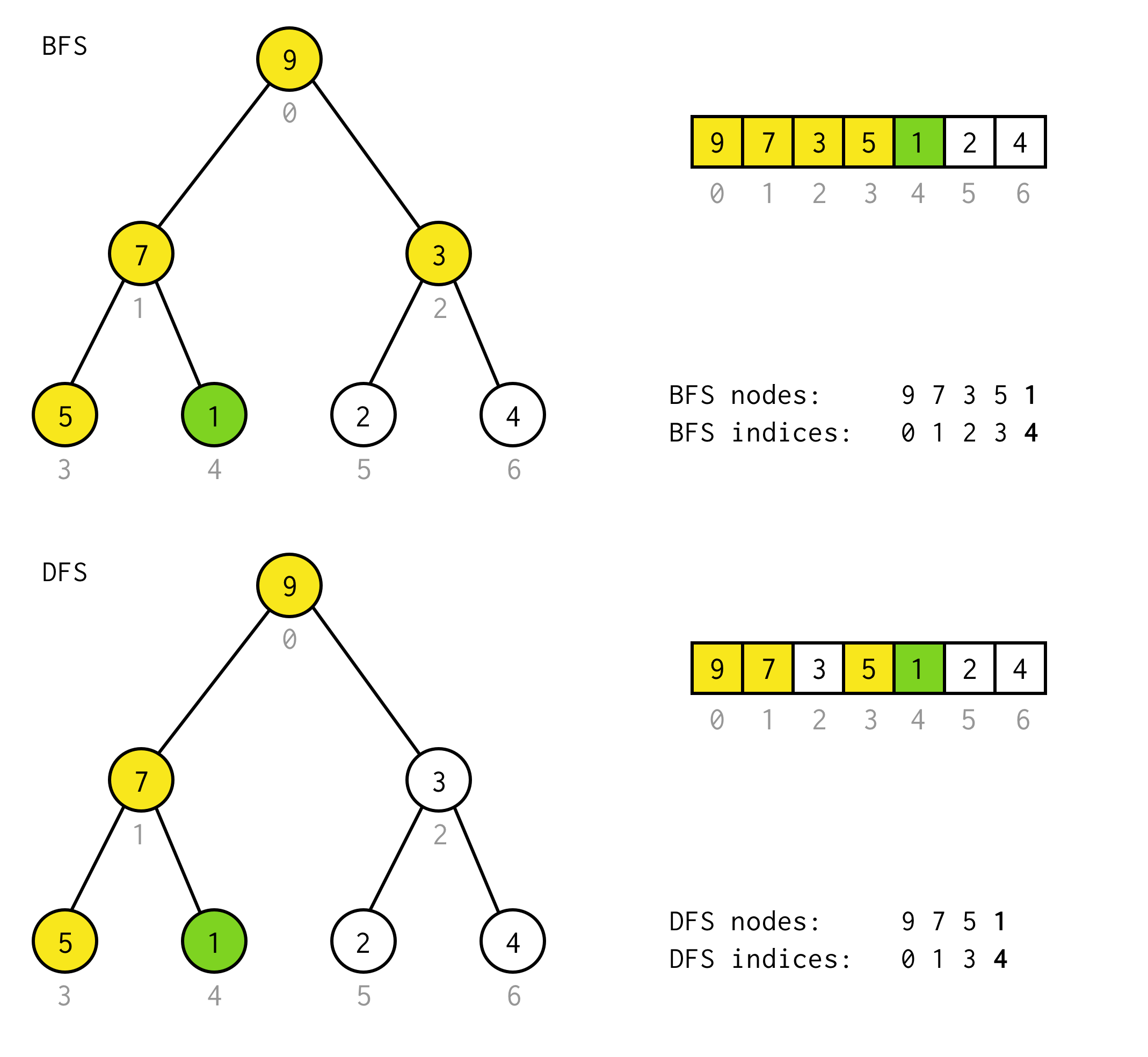
Gelbe Zellen sind Zellen, die im Suchalgorithmus getestet werden, bevor der benötigte Knoten gefunden wird.

Berücksichtigen Sie, dass DFS in einigen Fällen weniger Knoten zur Verarbeitung benötigt.Für einige Fälle erfordert es mehr.

BFS und DFS für Binärbaum-Array

Breadth-first search für Binärbaum-Array ist trivial.Da Elemente in Binärbaum-Array sind Ebene für Ebene platziert undbfs ist auch die Überprüfung Element Ebene für Ebene, bfs für Binärbaum-Array ist nur lineare Suche

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

Depth-first search ist ein bisschen schwieriger.

Bei der Verwendung einer Stack-Datenstruktur könnte man es genauso implementieren wie beim klassischen Binärbaum, einfach Indizes in den Stack legen.

Von diesem Punkt aus unterscheidet sich die Rekursion überhaupt nicht, man verwendet einfach den impliziten Methodenaufruf-Stack statt des Datenstruktur-Stacks.

Was wäre, wenn wir DFS ohne Stack und Rekursion implementieren könnten?

Nun, versuchen wir es.

DFS für Binary Tree Array (ohne Stack und Rekursion)

Wie in BFS beginnen wir mit dem Root Index 0.
Dann müssen wir sein linkes Kind inspizieren, dessen Index durch die Formel 2*i+1 berechnet werden kann.
Lassen Sie uns den Prozess des Gehens zum nächsten linken Kind verdoppeln.

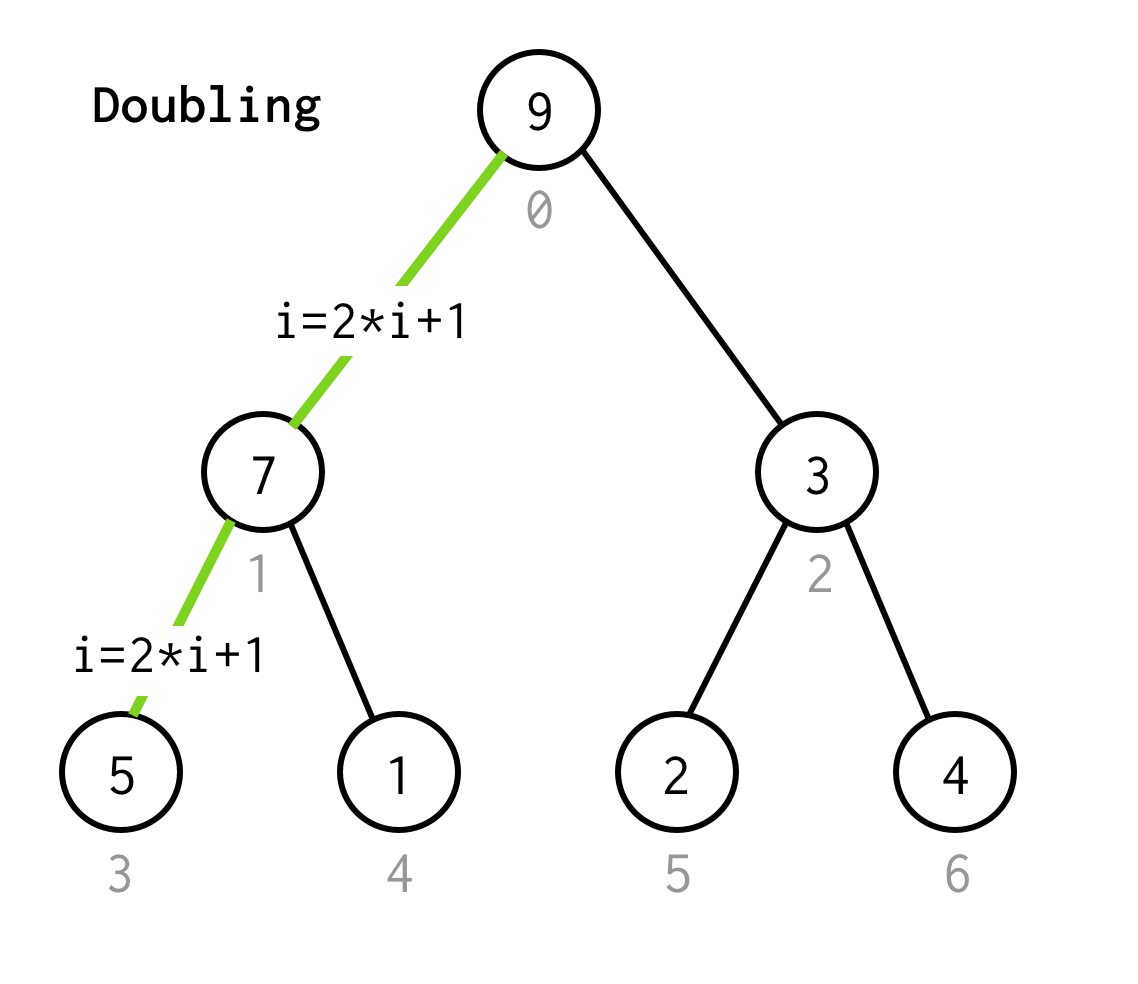
Wir fahren fort, den Index zu verdoppeln, bis wir nicht beim Blattknoten aufhören.

Wie können wir also verstehen, dass es ein Blattknoten ist?

Wenn das nächste linke Kind die Ausnahme „Index außerhalb der Array-Grenzen“ erzeugt, müssen wir mit der Verdopplung aufhören und zum rechten Kind springen.

Das ist eine gültige Lösung, aber wir können eine unnötige Verdopplung vermeiden.

Die Beobachtung hier ist, dass die Anzahl der Elemente im Baum von height zwei Mal größer ist (und plus eins) als der Baum mit height - 1.

Für den Baum mit height = 2 haben wir 7 Elemente, für den Baum mit height = 3 haben wir 7*2+1 = 15 Elemente.

Aufgrund dieser Beobachtung bilden wir eine einfache Bedingung

i < array.length / 2

Sie können überprüfen, ob diese Bedingung für jeden nicht-blättrigen Knoten im Baum gültig ist.

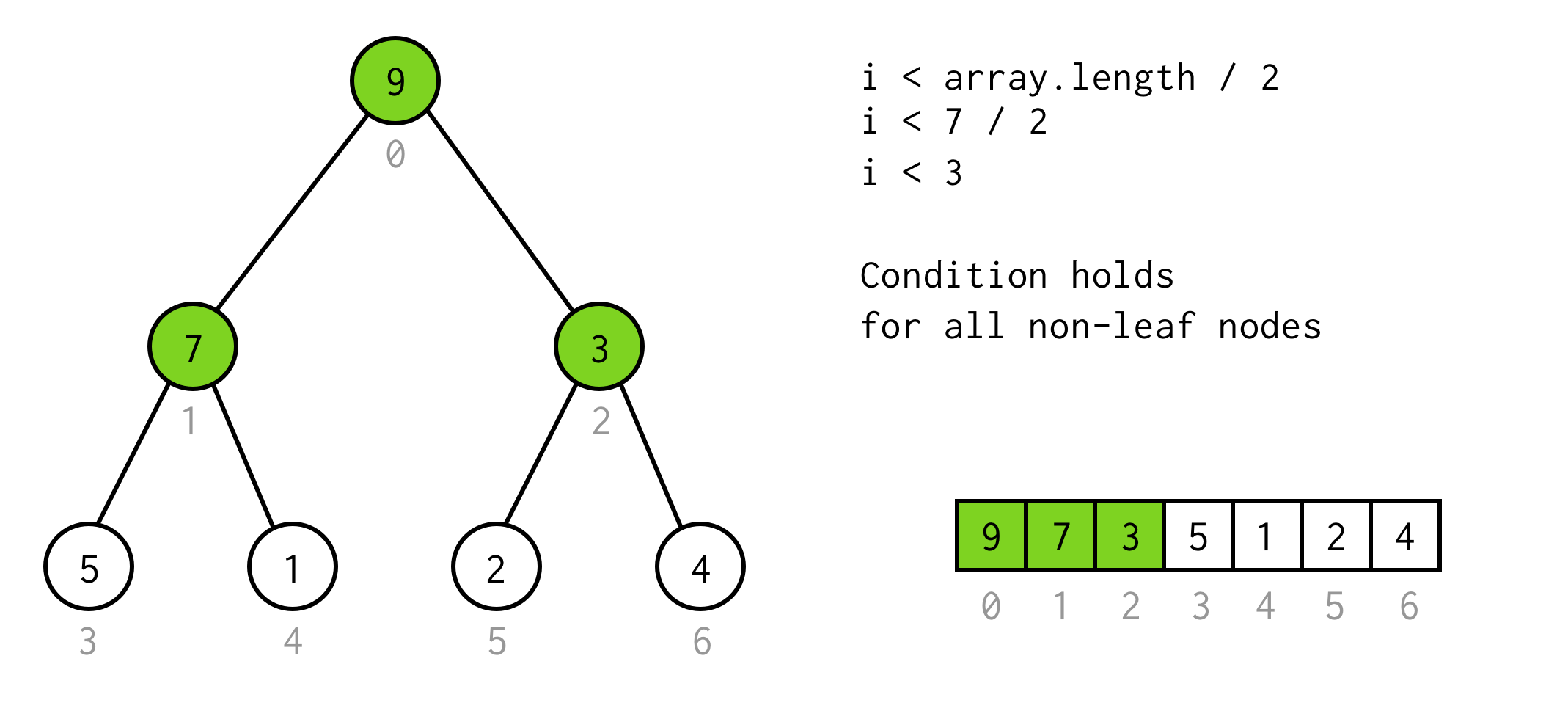
So weit so gut. Wir können die Verdopplung durchführen und wissen sogar, wann wir aufhören müssen.

Wenn wir an einem Blattknoten festhängen und die Verdopplung nicht mehr anwenden können, führen wir eine Sprungoperation durch.Im Grunde genommen, wenn die Verdopplung ist, gehen Sie zum linken Kind, Sprung ist, gehen Sie zum Elternteil und gehen Sie zum rechten Kind.

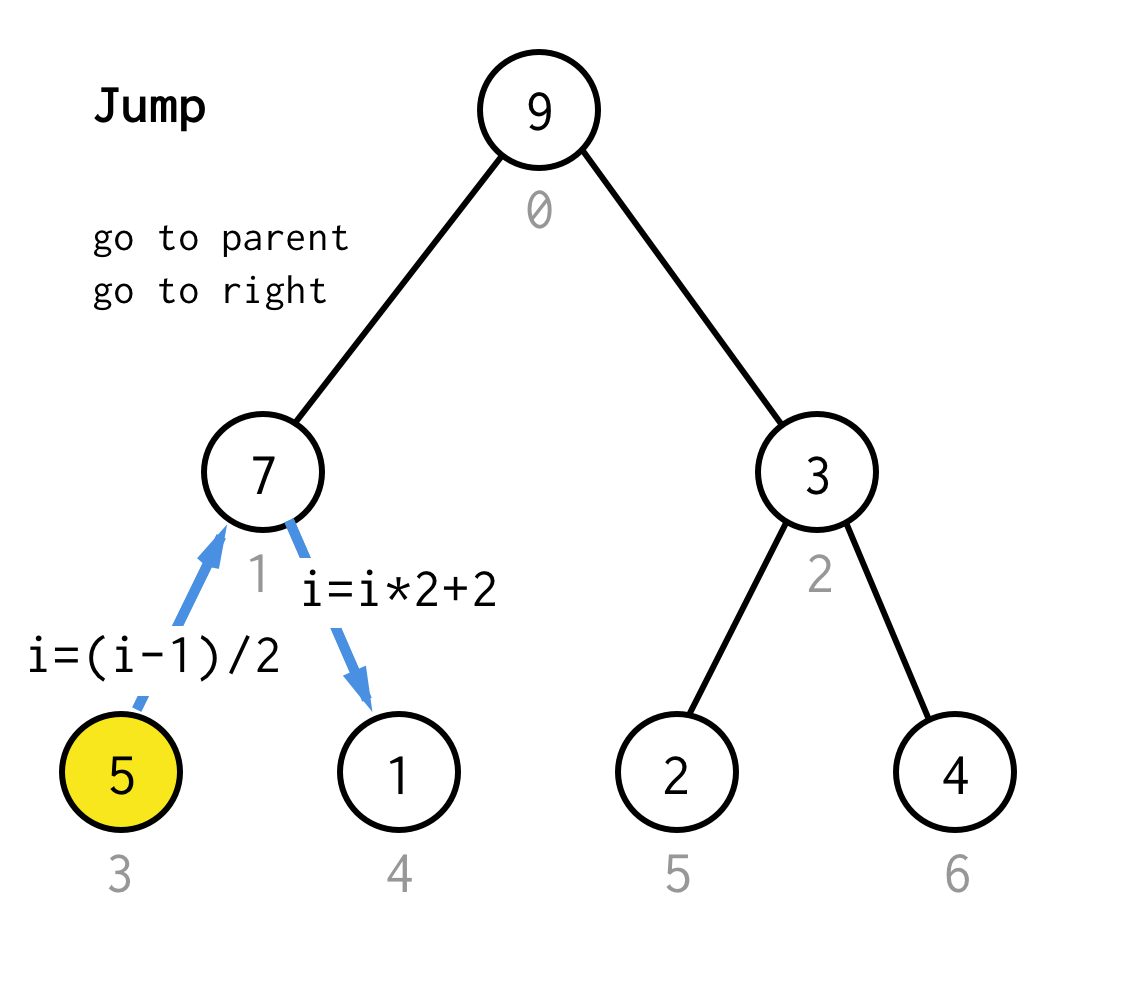
Solche Sprungoperation kann durch einfaches Inkrementieren des Blattindexes implementiert werden.Aber wenn wir am nächsten Blattknoten feststecken, bewegt das Inkrement den Knoten nicht zum nächsten Knoten, erforderlich für DFS.Also müssen wir einen doppelten Sprung durchführen

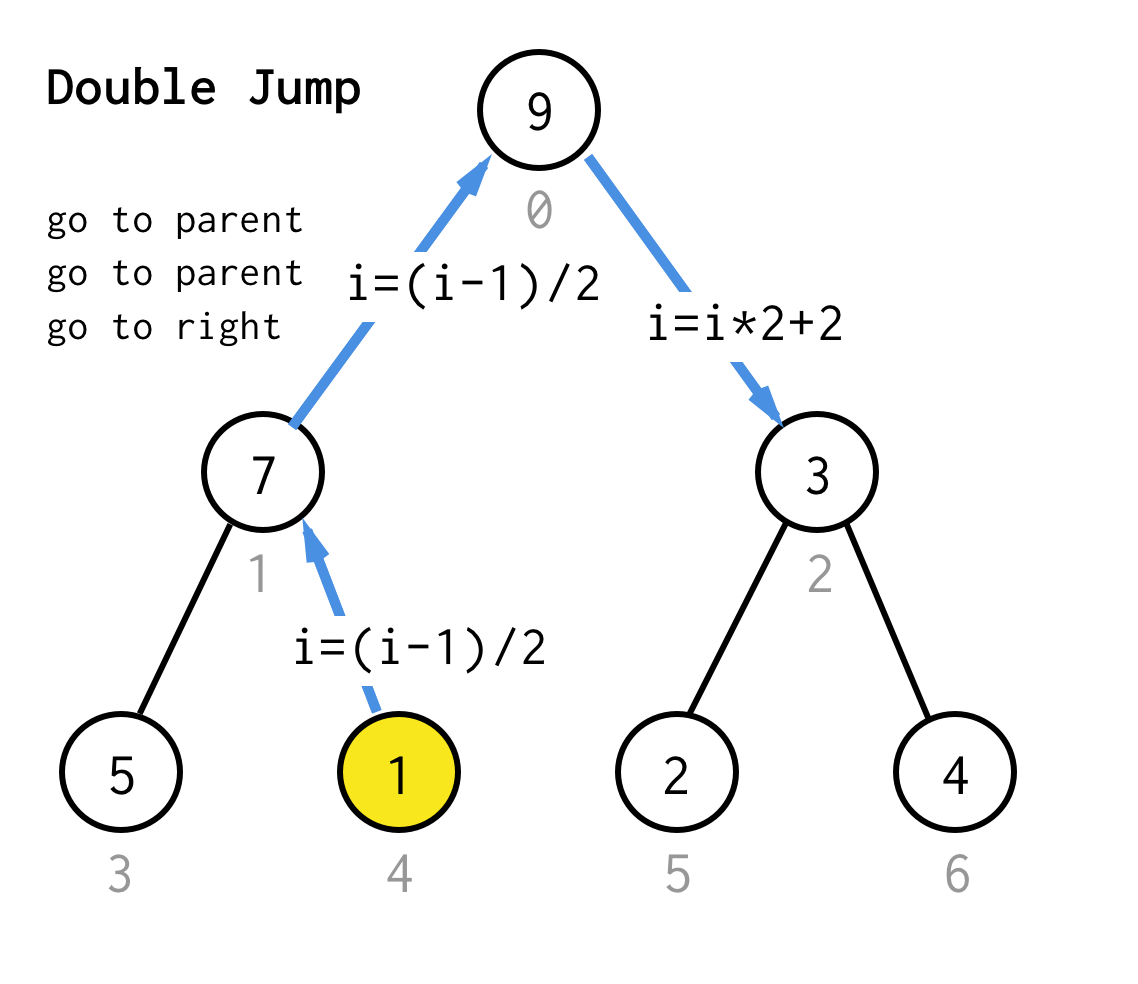
Um es allgemeiner zu machen, könnten wir für unseren Algorithmus die Operation jump N definieren, die angibt, wie viele Sprünge zum Elternteil erforderlich sind und immer mit einem Sprung zum richtigen Kind endet.

Für den Baum mit der Höhe 1 benötigen wir einen Sprung, Sprung 1

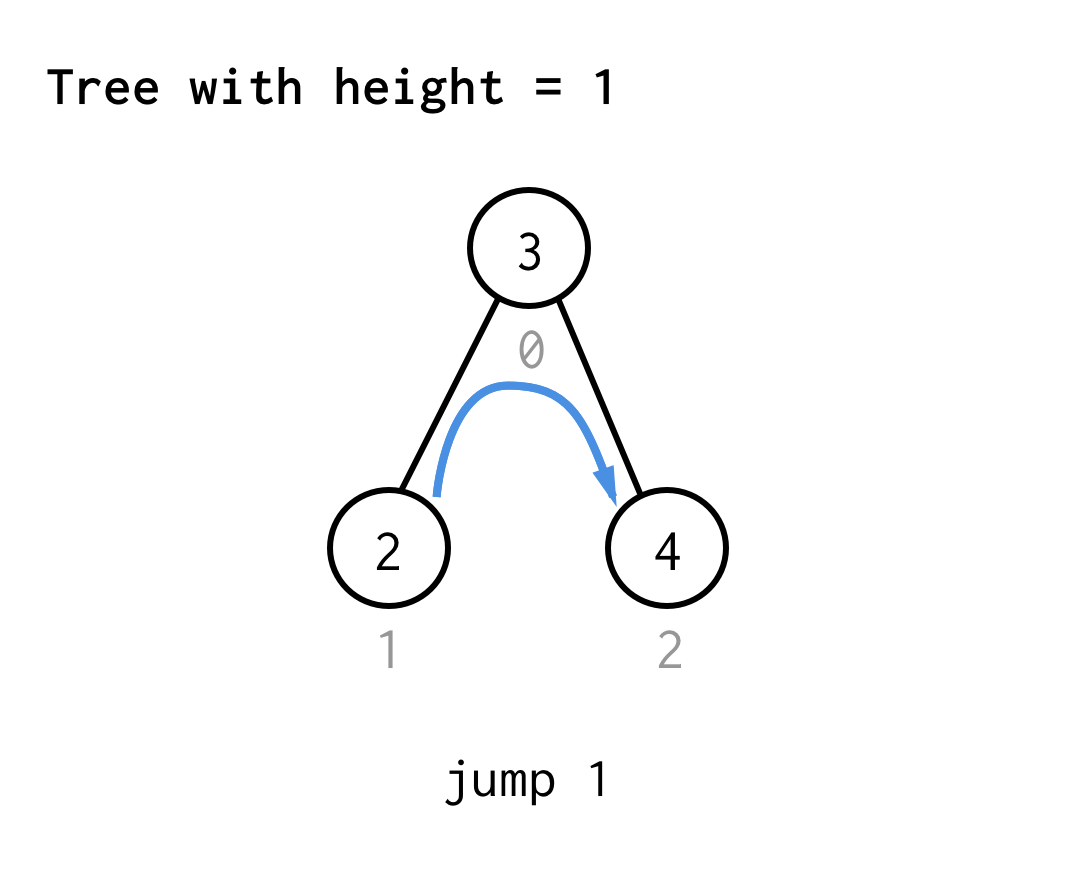
Für den Baum mit der Höhe 2 benötigen wir einen Sprung, einen Doppelsprung und dann wieder einen Sprung

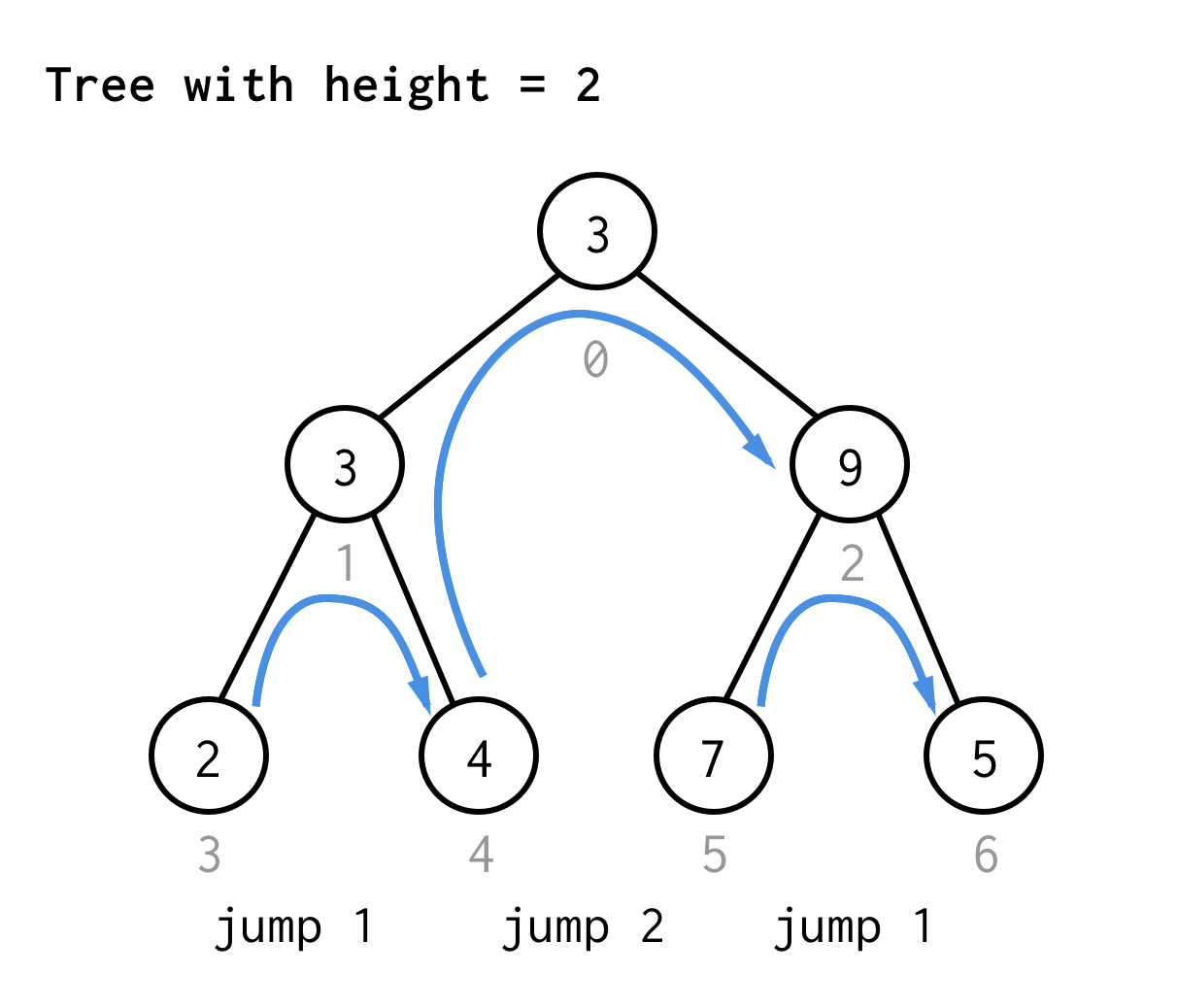
Für den Baum mit der Höhe 3 kann man die gleichen Regeln anwenden und erhält 7 Sprünge.

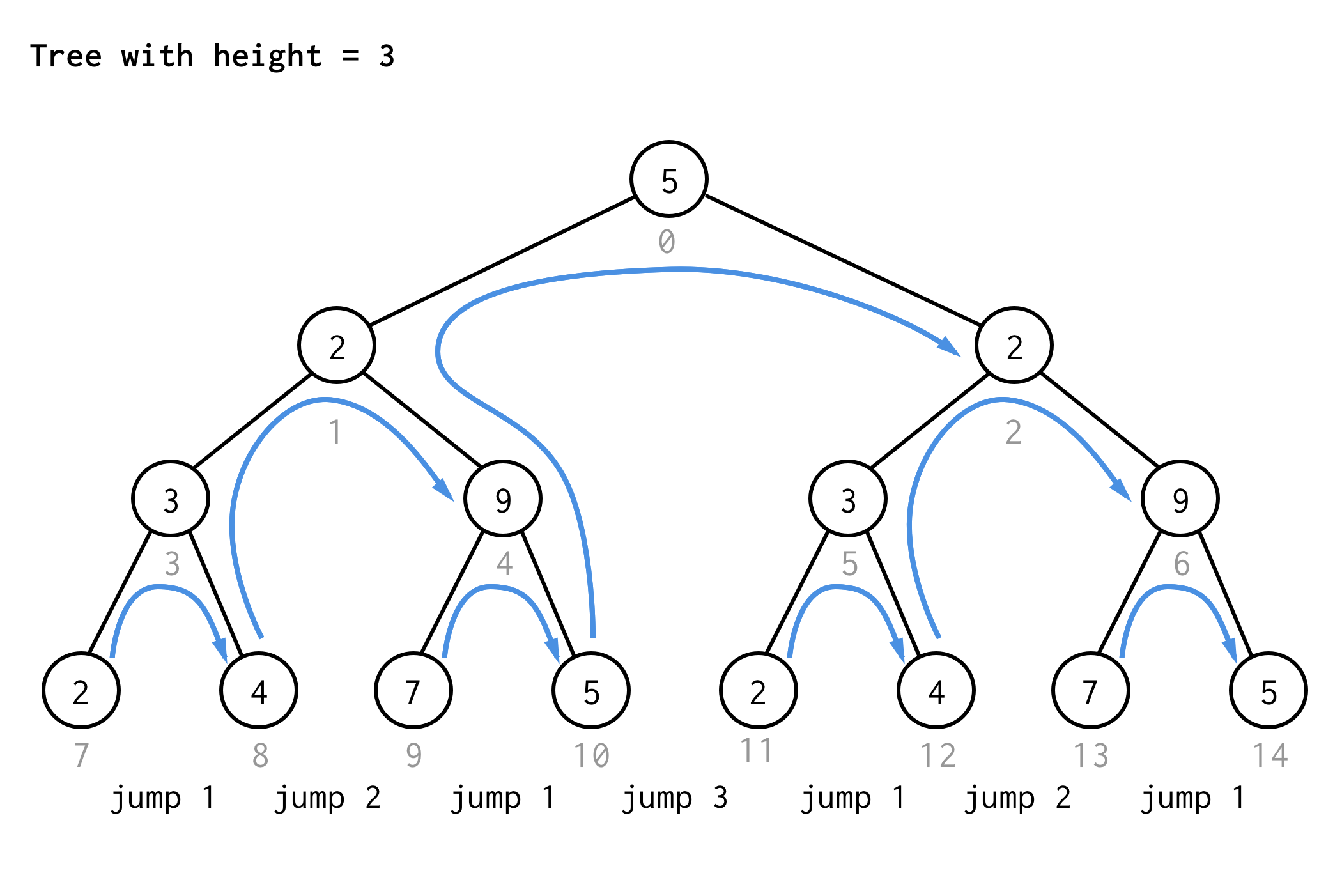
Siehst du das Muster?

Wenn man die gleiche Regel auf den Baum der Höhe 4 anwendet und nur die Sprungwerte aufschreibt, erhält man die nächste Sequenznummer

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Diese Sequenz ist als Zimin-Wort bekannt und hat eine rekursive Definition, was nicht so toll ist, weil wir keine Rekursion verwenden dürfen.

Lassen Sie uns einen anderen Weg finden, um sie zu berechnen.

Wenn Sie sich die Sprungfolge genau ansehen, können Sie ein nicht rekursives Muster erkennen.

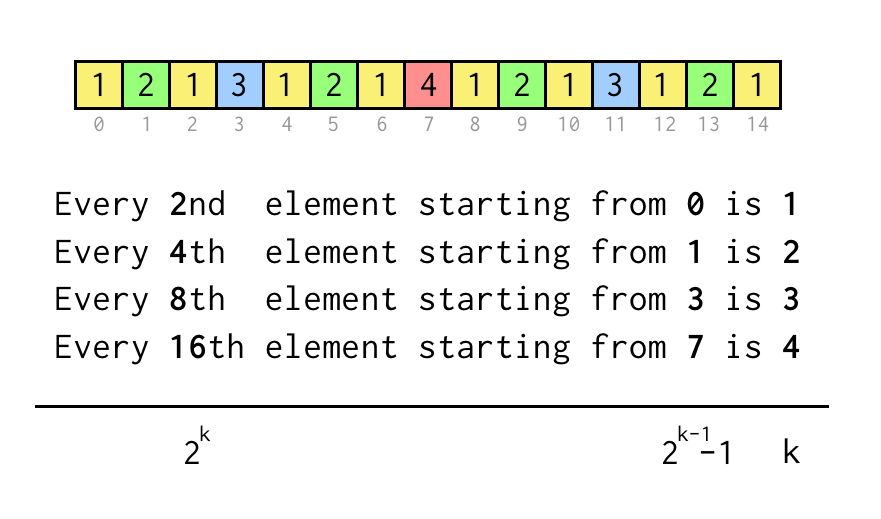
Wir können den Index für das aktuelle Blatt j verfolgen, der dem Index im obigen Sequenzfeld entspricht.

Um eine Aussage wie „Jedes 8. Element ab 3“ zu verifizieren, überprüfen wir einfach j % 8 == 3, wenn es wahr ist, werden drei Sprünge zum übergeordneten Knoten benötigt.

Iterativer Sprungprozess wird wie folgt ablaufen

• Beginnen Sie mit k = 1
• Springen Sie einmal zum übergeordneten Knoten, indem Sie i = (i - 1)/2
• Wenn leaf % 2*k == k - 1 alle Sprünge durchgeführt wurden, beenden Sie
• Ansonsten setzen Sie k auf 2*k und wiederholen Sie.

Wenn du alles zusammensetzt, was wir besprochen haben

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Erledigt. DFS für binäres Baumarray ohne Stack und Rekursion

Komplexität

Die Komplexität sieht quadratisch aus, weil wir eine Schleife in einer Schleife haben, aber schauen wir mal, wie die Realität aussieht.

• Für die Hälfte der Gesamtknoten (n/2) verwenden wir die Verdoppelungsstrategie, die konstant ist O(1)
• Für die andere Hälfte der Gesamtknoten (n/2) verwenden wir die Blattsprungstrategie.
• Die Hälfte der Blattsprungknoten (n/4) erfordert nur einen Elternsprung, also eine Iteration. O(1)
• Die Hälfte dieser Hälfte (n/8) erfordert zwei Sprünge, also 2 Iterationen. O(1)
• …
• Nur ein springender Blattknoten erfordert einen vollen Sprung zur Wurzel, nämlich O(logN)
• Wenn also alle Fälle O(1) haben, außer einem, der O(logN) ist, können wir sagen, dass der Durchschnitt für den Sprung O(1)
• Gesamtkomplexität ist O(n)

Leistung

Obwohl die Theorie gut ist, wollen wir sehen, wie dieser Algorithmus in der Praxis funktioniert, indem wir ihn mit anderen vergleichen.

Wir testen 5 Algorithmen, die JMH verwenden.

• BFS auf Binärbaum (verkettete Liste als Warteschlange)
• BFS auf Binärbaum-Array (lineare Suche)
• DFS auf Binärbaum (Stapel)
• DFS on Binary Tree Array (stack)
• Iterative DFS on Binary Tree Array

Wir haben einen Baum erstellt und verwenden ein Prädikat, um den letzten Knoten zu finden,um sicherzustellen, dass wir immer die gleiche Anzahl von Knoten für alle Algorithmen treffen.

So, Ergebnisse

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Es ist offensichtlich, dass BFS auf Array gewinnt. Es ist nur eine lineare Suche, wenn man also einen Binärbaum als Array darstellen kann, sollte man das tun.

Iteratives DFS, das wir gerade im Artikel beschrieben haben, belegt 2den zweiten Platz und ist 4.5mal langsamer als die lineare Suche (BFS auf Array)

Die übrigen drei Algorithmen sind sogar noch langsamer als iteratives DFS, wahrscheinlich, weil sie zusätzliche Datenstrukturen, zusätzlichen Platz und Speicherzuweisung erfordern.

Und der schlechteste Fall ist BFS auf Binärbaum. Ich vermute, dass hier die verknüpfte Liste ein Problem ist.

Fazit

Binary Tree Array ist ein netter Trick, um hierarchische Datenstrukturen als statisches Array (zusammenhängender Bereich im Speicher) darzustellen. Es definiert eine einfache Indexbeziehung für den Wechsel vom Elternteil zum Kind und vom Kind zum Elternteil, was bei der klassischen binären Array-Darstellung nicht möglich ist. Es gibt einige Nachteile, wie z.B. langsames Einfügen/Löschen, aber ich bin sicher, dass es viele Anwendungen für Binärbaum-Arrays gibt.

Wie wir gezeigt haben, sind Suchalgorithmen, BFS und DFS, die auf Arrays implementiert sind, viel schneller als ihre Brüder auf einer referenzbasierten Struktur. Für reale Probleme ist das nicht so wichtig, und wahrscheinlich werde ich immer noch das referenzbasierte binäre Array verwenden.

Alles in allem, es war eine nette Übung. Erwarte die Frage „DFS auf binärem Array ohne Rekursion und Stack“ bei deinem nächsten Interview.

• Algorithmen
• Datenstrukturen
• Programmierung

mishadoff 10. September 2017