Eigenvektor

Eigenvektoren sind eine spezielle Menge von Vektoren, die mit einem linearen Gleichungssystem verbunden sind (i.e., einer Matrixgleichung), die manchmal auch als charakteristische Vektoren, Eigenvektoren oder latente Vektoren bezeichnet werden (Marcus und Minc 1988, S. 144).

Die Bestimmung der Eigenvektoren und Eigenwerte eines Systems ist in der Physik und den Ingenieurwissenschaften äußerst wichtig, da sie einer Matrixdiagonalisierung gleichkommt und in so häufigen Anwendungen wie der Stabilitätsanalyse, der Physik rotierender Körper und kleinen Schwingungen vibrierender Systeme vorkommt, um nur einige zu nennen. Jedem Eigenvektor ist ein entsprechender so genannter Eigenwert zugeordnet. Mathematisch gesehen müssen zwei verschiedene Arten von Eigenvektoren unterschieden werden: linke Eigenvektoren und rechte Eigenvektoren. Für viele Probleme in der Physik und im Ingenieurwesen ist es jedoch ausreichend, nur die rechten Eigenvektoren zu betrachten. Der Begriff „Eigenvektor“, der in solchen Anwendungen ohne Einschränkung verwendet wird, kann daher so verstanden werden, dass er sich auf einen rechten Eigenvektor bezieht.

Die Zerlegung einer quadratischen Matrix in Eigenwerte und Eigenvektoren wird in dieser Arbeit als Eigenwertzerlegung bezeichnet, und die Tatsache, dass diese Zerlegung immer möglich ist, solange die aus den Eigenvektoren von bestehende Matrix quadratisch ist, ist als Eigenwertzerlegungssatz bekannt.

Definiere einen rechten Eigenvektor als einen Spaltenvektor , der

(1)

wobei eine Matrix ist, so

(2)

was bedeutet, dass die rechten Eigenwerte die Determinante Null haben müssen, d. h.e.,

(3)

In ähnlicher Weise definieren wir einen linken Eigenvektor als einen Zeilenvektor , der

(4)

Die Transponierung jeder Seite ergibt

(5)

was umgeschrieben werden kann als

(6)

Durch erneute Umordnung erhält man

(7)

das bedeutet

(8)

Umschreiben ergibt

			(9)
			(10)
			(11)

wobei der letzte Schritt aus der Identität

(12)

Die Gleichungen (◇) und (11), die beide gleich 0 für beliebige und sind, erfordern daher, dass , d.h., linke und rechte Eigenwerte sind äquivalent, eine Aussage, die für Eigenvektoren nicht gilt.

Sei eine Matrix, die durch die Spalten der rechten Eigenvektoren gebildet wird und eine Matrix, die durch die Zeilen der linken Eigenvektoren gebildet wird. Sei

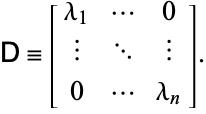(13)

Dann

			(14)
			(15)

und

			(16)
			(17)

so

(18)

Aber diese Gleichung ist von der Form

(19)

wobei eine Diagonalmatrix ist, also muss es wahr sein, dass auch diagonal ist. Insbesondere, wenn eine symmetrische Matrix ist, dann sind der linke und der rechte Eigenvektor einfach die Transponierung des jeweils anderen, und wenn eine selbstadjungierte Matrix ist (d.h. sie ist hermitisch), dann sind der linke und der rechte Eigenvektor adjungierte Matrizen.

Eigenvektoren dürfen nicht gleich dem Nullvektor sein. Ein skalares Vielfaches eines Eigenvektors, das nicht Null ist, ist äquivalent zum ursprünglichen Eigenvektor. Daher werden Eigenvektoren ohne Verlust der Allgemeingültigkeit oft auf Einheitslänge normiert.

Während eine -Matrix immer Eigenwerte hat, von denen einige oder alle entartet sein können, kann eine solche Matrix zwischen 0 und linear unabhängige Eigenvektoren haben. Zum Beispiel hat die Matrix nur den einzigen Eigenvektor .

Eigenvektoren können in der Wolfram Language mit Eigenvectors berechnet werden. Dieser Befehl gibt immer eine Liste der Länge zurück, so dass alle Eigenvektoren, die nicht linear unabhängig sind, als Nullvektoren zurückgegeben werden. Eigenvektoren und Eigenwerte können mit dem Befehl Eigensystem zusammen zurückgegeben werden.

Gibt eine -Matrix mit den Eigenvektoren , und und den entsprechenden Eigenwerten , , und , dann kann ein beliebiger Vektor geschrieben werden

(20)

Anwendung der Matrix ,

			(21)
			(22)

so

(23)

Wenn , und , so folgt daraus, dass

(24)

so führt die wiederholte Anwendung der Matrix auf einen beliebigen Vektor erstaunlicherweise zu einem Vektor, der proportional zu dem Eigenvektor mit dem größten Eigenwert ist.