Eigenschaften der Winkel eines Dreiecks

Verwandte Themen:
Weitere Geometrie-Lektionen
Geometrie-Arbeitsblätter
Geometrie-Spiele
In diesen Lektionen werden wir eine Zusammenfassung der Eigenschaften der Winkel eines Dreiecks geben.

• Dreieckssummensatz – Die Summe der 3 Winkel in einem Dreieck ist immer 180°
• Die Summe eines Innenwinkels und seines angrenzenden Außenwinkels ist 180°
• Außenwinkelsatz – Ein Außenwinkel eines Dreiecks ist gleich der Summe der beiden gegenüberliegenden Innenwinkel
• Ein gleichseitiges Dreieck hat 3 gleiche Winkel, die jeweils 60° betragen. Ein gleichschenkliges Dreieck hat 2 gleiche Winkel, das sind die Winkel, die den 2 gleichen Seiten gegenüberliegen

Die Winkel eines Dreiecks haben die folgenden Eigenschaften:

Eigenschaft 1: Dreieckssummensatz

Die Summe der 3 Winkel in einem Dreieck ist immer 180°.

Beispiel:

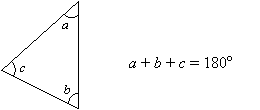
Wie beweist man den Dreieckssummensatz?
Das folgende Video zeigt, wie man beweist, dass die Summe der Winkel eines Dreiecks 180 Grad beträgt. (Dreieckssummensatz)

• Schrittweise Lösungen anzeigen

Wie findet man den fehlenden Winkel in einem Dreieck mit Hilfe des Dreieckssummensatzes?
Schritt 1: Schreibe die Gleichung auf, indem du alle Winkel addierst und sie gleich 180° machst.
Schritt 2: Löse für x.
Schritt 3: Substituiere, um die fehlenden Winkel zu finden.

• Zeige Schritt-für-Schritt-Lösungen

Eigenschaft 2:

Die Summe eines Innenwinkels und seines angrenzenden Außenwinkels ist 180°.

Beispiel:

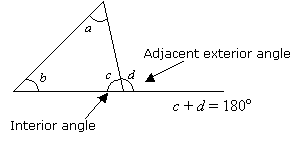
Eigenschaft 3: Außenwinkeltheorem

Ein Außenwinkel eines Dreiecks ist gleich der Summe der beiden gegenüberliegenden Innenwinkel.

Beispiel:

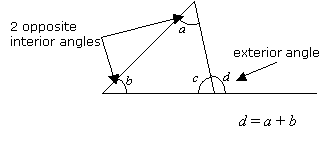
Außenwinkel eines Dreiecks
Finden des unbekannten Winkels eines Dreiecks
Beispiel:
1. Berechne das Dreieck abc, wobei a = 40° und b = 60° ist. Wie groß ist der Außenwinkel zu ∠acb?
2. Berechne das Dreieck abc, bei dem a = 50° und b = 30° ist. Wie groß ist der Außenwinkel zu ∠acb?
2. Berechne das Dreieck abc, bei dem a = 90° und b = 40° ist. Wie lautet der Außenwinkel zu ∠acb?

• Schrittweise Lösungen anzeigen

Wie kann man den Außenwinkelsatz anwenden, um Probleme mit Winkeln in einem Dreieck zu lösen?

• Schrittweise Lösungen anzeigen

Eigenschaft 4:

Ein gleichseitiges Dreieck hat 3 gleiche Winkel, die jeweils 60° betragen.
Ein gleichschenkliges Dreieck hat 2 gleiche Winkel, das sind die Winkel gegenüber den 2 gleichen Seiten.
Wie findet man den fehlenden Winkel in einem gleichschenkligen Dreieck?

• Schrittweise Lösungen anzeigen

Parallele Linien und der Winkel-Summen-Satz des Dreiecks

• Schrittweise Lösungen anzeigen

Die oben genannten Winkeleigenschaften können uns helfen, unbekannte Winkel in einem Dreieck zu finden.

Beispiel:

Finde den Wert von x in folgendem Dreieck.

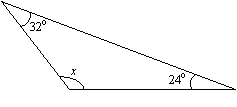
Lösung:

x + 24° + 32° = 180° (Summe der Winkel ist 180°)
x + 56° = 180°
x = 180° – 56° = 124°

Beispiel:

Finde die Werte von x und y in folgendem Dreieck.

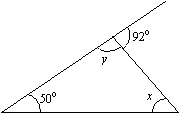
Lösung:

x + 50° = 92° (Summe der gegenüberliegenden Innenwinkel = Außenwinkel)
x = 92° – 50° = 42°

y + 92° = 180° (Innenwinkel + angrenzender Außenwinkel = 180°.)
y = 180° – 92° = 88°

Testen Sie den kostenlosen Mathway-Rechner und Problemlöser unten, um verschiedene mathematische Themen zu üben. Probieren Sie die vorgegebenen Beispiele aus oder geben Sie Ihre eigene Aufgabe ein und überprüfen Sie Ihre Antwort anhand der schrittweisen Erklärungen.