Algebră > Algebră liniară > Matrice > Matrice > Matrice Valori proprii >
Algebră > Algebră liniară > Matrice > Matrice > Matrice Descompunere >

EXPLORĂ acest subiect în sala de clasă MathWorld

Vectori proprii sunt un set special de vectori asociați cu un sistem liniar de ecuații (i.e., o ecuație matricială) care sunt uneori cunoscuți și sub numele de vectori caracteristici, vectori proprii sau vectori latenți (Marcus și Minc 1988, p. 144).

Determinarea vectorilor proprii și a valorilor proprii ale unui sistem este extrem de importantă în fizică și inginerie, unde este echivalentă cu diagonalizarea matricei și apare în aplicații comune precum analiza stabilității, fizica corpurilor în rotație și oscilațiile mici ale sistemelor vibrante, pentru a numi doar câteva. Fiecare vector propriu este asociat cu o așa-numită valoare proprie corespunzătoare. Din punct de vedere matematic, trebuie să se facă distincția între două tipuri diferite de vectori proprii: vectori proprii de stânga și vectori proprii de dreapta. Cu toate acestea, pentru multe probleme din fizică și inginerie, este suficient să se ia în considerare doar vectorii proprii drepți. Prin urmare, termenul „vector propriu” utilizat fără rezerve în astfel de aplicații poate fi înțeles ca referindu-se la un vector propriu drept.

Descompunerea unei matrice pătrate A în valori proprii și vectori proprii este cunoscută în această lucrare ca descompunere proprie, iar faptul că această descompunere este întotdeauna posibilă atâta timp cât matricea formată din vectorii proprii ai A este pătrată este cunoscută sub numele de teorema descompunerii proprii.

Definiți un vector propriu drept ca fiind un vector coloană X_R care satisface

AX_R=lambda_RX_R,
(1)

unde A este o matrice, deci

(A-lambda_RI)X_R=0,
(2)

ceea ce înseamnă că valorile proprii din dreapta trebuie să aibă determinant zero, i.e.e.,

det(A-lambda_RI)=0.
(3)

În mod similar, se definește un vector propriu stâng ca fiind un vector de rând X_L care satisface

X_LA=lambda_LX_L.
(4)

Făcând transpunerea fiecărei părți rezultă

(X_LA)^(T)=lambda_LX_L^(T),
(5)

care poate fi rescrisă sub forma

A^(T)X_L^(T)=lambda_LX_L^(T).
(6)

Se rearanjează din nou pentru a obține

(A^(T)-lambda_LI)X_L^(T)=0,
(7)

ceea ce înseamnă

det(A^(T)-lambda_LI)=0.
(8)

Rezcriind rezultă

0=det(A^(T)-lambda_LI) = det(A^(T)-lambda_LI^(T))
(9)
= det(A-lambda_LI)^(T)
(10)
= det(A-lambda_LI),
(11)

unde ultimul pas rezultă din identitatea

det(A)=det(A^(T)).
(12)

Încadrarea ecuațiilor (◇) și (11), care sunt ambele egale cu 0 pentru A și X arbitrare, impune deci că lambda_R=lambda_L=lambda, adică, valorile proprii din stânga și din dreapta sunt echivalente, afirmație care nu este adevărată pentru vectorii proprii.

Să fie X_R matricea formată din coloanele vectorilor proprii din dreapta și X_L matricea formată din rândurile vectorilor proprii din stânga. Fie

D=.
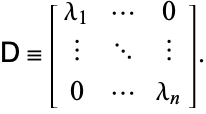(13)

Atunci

.

.

AX_R = X_RD
(14)
X_LA = DX_L DX_L
(15)

și

.

X_LAX_R = X_LX_RD
(16)
X_LAX_R = DX_LX_R,
(17)

so

X_LX_RD=DX_LX_R.
(18)

Dar această ecuație este de forma

.

CD=DC
(19)

unde D este o matrice diagonală, deci trebuie să fie adevărat că C=X_LX_R este, de asemenea, diagonală. În special, dacă A este o matrice simetrică, atunci vectorii proprii din stânga și din dreapta sunt pur și simplu transpuse unul altuia, iar dacă A este o matrice autoadjunctă (adică este hermitiană), atunci vectorii proprii din stânga și din dreapta sunt matrici adiacente.

Vectorii proprii pot să nu fie egali cu vectorul zero. Un multiplu scalar diferit de zero al unui vector propriu este echivalent cu vectorul propriu original. Prin urmare, fără a pierde din generalitate, vectorii proprii sunt adesea normalizați la lungimea unitară.

În timp ce o matrice n×n are întotdeauna n valori proprii, dintre care unele sau toate pot fi degenerate, o astfel de matrice poate avea între 0 și n vectori proprii liniar independenți. De exemplu, matricea are doar un singur vector propriu (1,0).

Vectorii proprii pot fi calculați în limbajul Wolfram folosind Eigenvectors. Această comandă returnează întotdeauna o listă de lungime n, astfel încât orice vectori proprii care nu sunt liniar independenți sunt returnați ca vectori zero. Vectorii proprii și valorile proprii pot fi returnate împreună folosind comanda Eigensystem.

Dată o matrice 3×3 A cu vectorii proprii x_1, x_2 și x_3 și valorile proprii corespunzătoare lambda_1, lambda_2, și lambda_3, atunci un vector arbitrar y poate fi scris

y=b_1x_1+b_2x_2+b_3x_3.
(20)

Aplicând matricea A,

.

Ay = b_1Ax_1+b_2Ax_2+b_3Ax_3
(21)
= lambda_1(b_1x_1+(lambda_2)/(lambda_1)b_2x_2+(lambda_3)/(lambda_1)b_3x_3),
(22)

asadar

A^ny=lambda_1^n.
(23)

Dacă lambda_1lambda_2,lambda_3, și b_1!=0, rezultă deci că

lim_(n-infty)A^ny=lambda_1^nb_1x_1,
(24)

astfel încât aplicarea repetată a matricei la un vector arbitrar în mod uimitor are ca rezultat un vector proporțional cu vectorul propriu cu cea mai mare valoare proprie.