Privacy & Cookies
Acest site folosește cookies. Continuând, sunteți de acord cu utilizarea acestora. Aflați mai multe, inclusiv cum să controlați cookie-urile.
O spirală este o curbă care „emană dintr-un punct, îndepărtându-se pe măsură ce se învârte în jurul punctului”.

Există multe tipuri diferite de spirale, în funcție de formulele care le creează. În această postare pe blog, voi discuta despre spiralele bidimensionale (rețineți că există, de asemenea, o varietate de spirale tridimensionale).
Spirala lui Arhimede
Este o spirală numită după faimosul matematician grec Arhimede, care a fost primul care a descris-o în cartea sa Despre spirale. Este descrisă de următoarea ecuație polară:
unde a și b sunt numere reale.
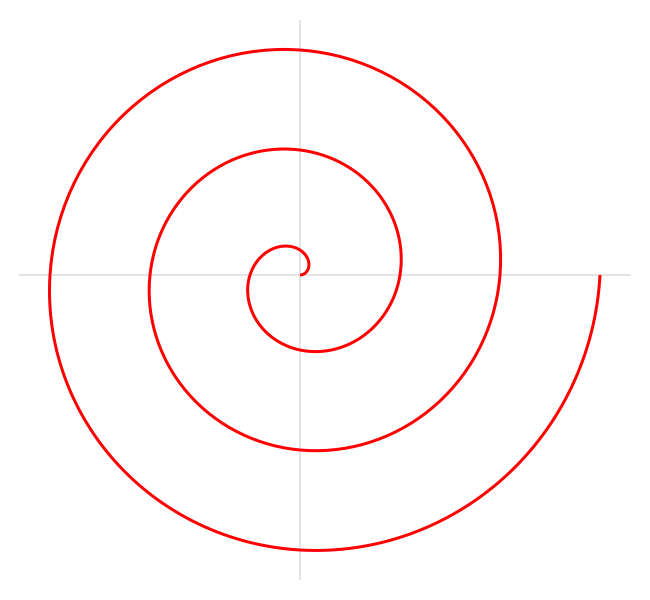
Cu modificarea parametrului a, spirala se va roti, iar parametrul b controlează distanța dintre rotațiile succesive.
Spirala lui Fermat
Spirala lui Fermat este o spirală parabolică care se supune următoarei ecuații polare:
Este un tip de spirală arhimedică.

Spirala lui Euler
Cunoscută și sub numele de spirală Cornu, este o curbă a cărei curbură crește pe măsură ce crește distanța față de origine; „curbura unei curbe circulare este egală cu reciproca razei”.

Forma parametrică constă în două ecuații cu intervale de Fresnel, care pot fi rezolvate doar aproximativ.
Aceste integrale, și deci spirala lui Euler, pot fi folosite pentru a descrie distribuția de energie a difracției lui Fresnel la o singură fantă în teoria undelor.
Spirala hiperbolică
Concepută pentru prima dată de Pierre Varignon în 1704, spirala hiperbolică este o curbă transcendentală, ceea ce înseamnă că „este o funcție analitică ce nu satisface o ecuație polinomială”. Ea este opusul spiralei arhimediene și astfel are următoarea ecuație polară:
În centru, ea se află la o distanță infinită de pol; pentru θ care începe la 0, r începe la infinit.
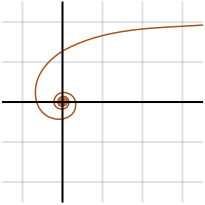
Lituus
Lituus este o spirală cu ecuația polară:
unde k este o constantă. Prin urmare, unghiul este invers proporțional cu pătratul razei. 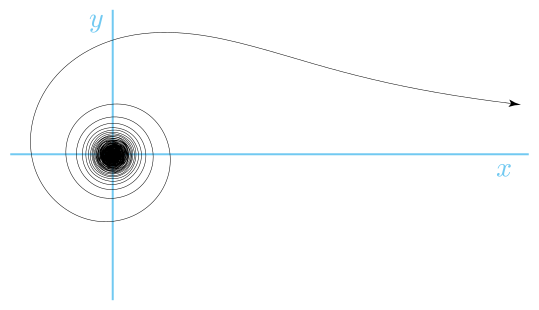
Curba a fost numită de Roger Cotes, într-o colecție de lucrări publicate în 1722, după vechiul lituus roman (un toiag augural curbat sau trompetă de război).
Spirala logaritmică
 Spirala logaritmică este o spirală autosimilară, care apare adesea în natură. A fost descrisă pentru prima dată de Descartes, dar a fost studiată în profunzime de Jacob Bernoulli, care a numit-o „spirala minunată”. Ea are o ecuație polară de
Spirala logaritmică este o spirală autosimilară, care apare adesea în natură. A fost descrisă pentru prima dată de Descartes, dar a fost studiată în profunzime de Jacob Bernoulli, care a numit-o „spirala minunată”. Ea are o ecuație polară de
.





Lasă un răspuns