gânduri de Mishadoff

Implementarea căutării în profunzime pentru arborele binar fără stivă și recursivitate.

Array arbore binar

Acesta este un arbore binar.

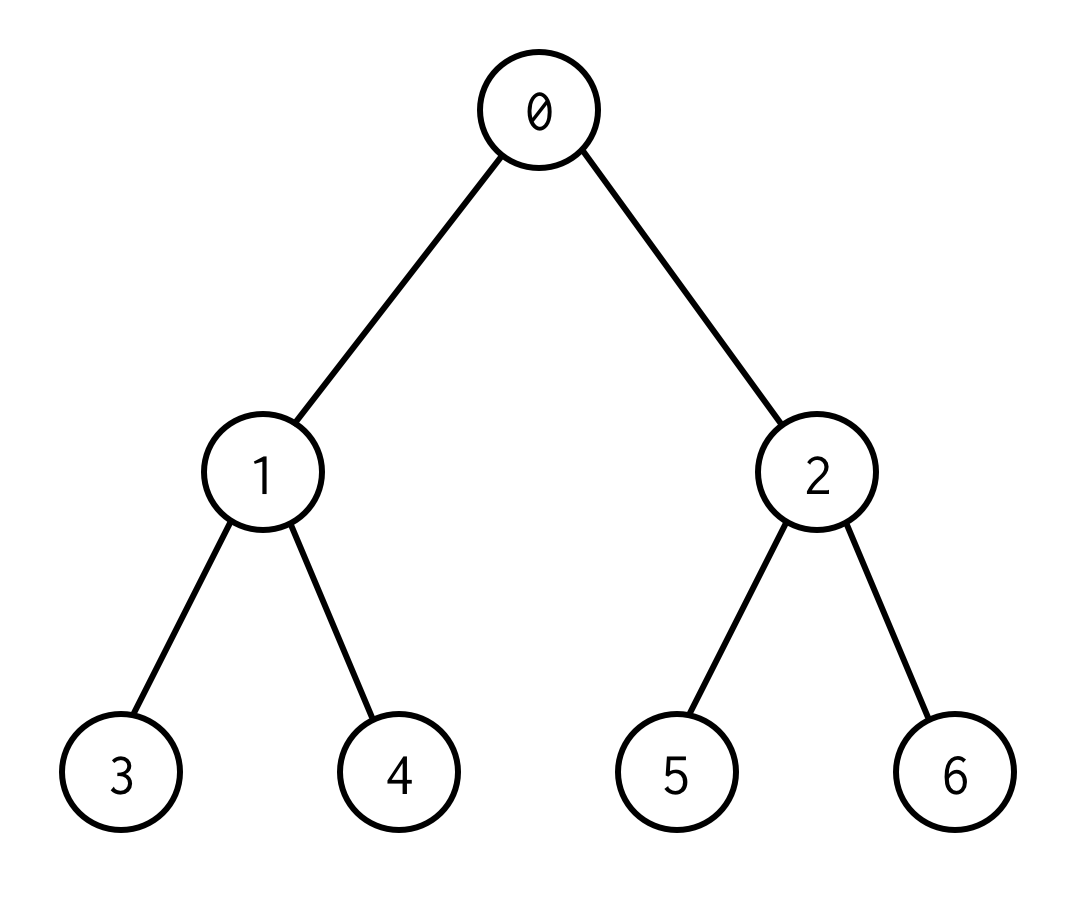
0 este un nod rădăcină.
0 are doi copii: stânga 1 și dreapta: 2.
Care dintre copiii săi are copiii lor și așa mai departe.
Nodurile fără copii sunt noduri frunză (3,4,5,6).

Numărul de muchii între nodurile rădăcină și nodurile frunză definește înălțimea arborelui.Arborele de mai sus are înălțimea 2.

Abordarea standard pentru a implementa arborele binar este de a defini clasa numită BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Cu toate acestea, există un truc pentru a implementa arborele binar folosind doar array-uri statice.Dacă enumerați toate nodurile din arborele binar pe niveluri începând de la zero, le puteți împacheta în array-uri.

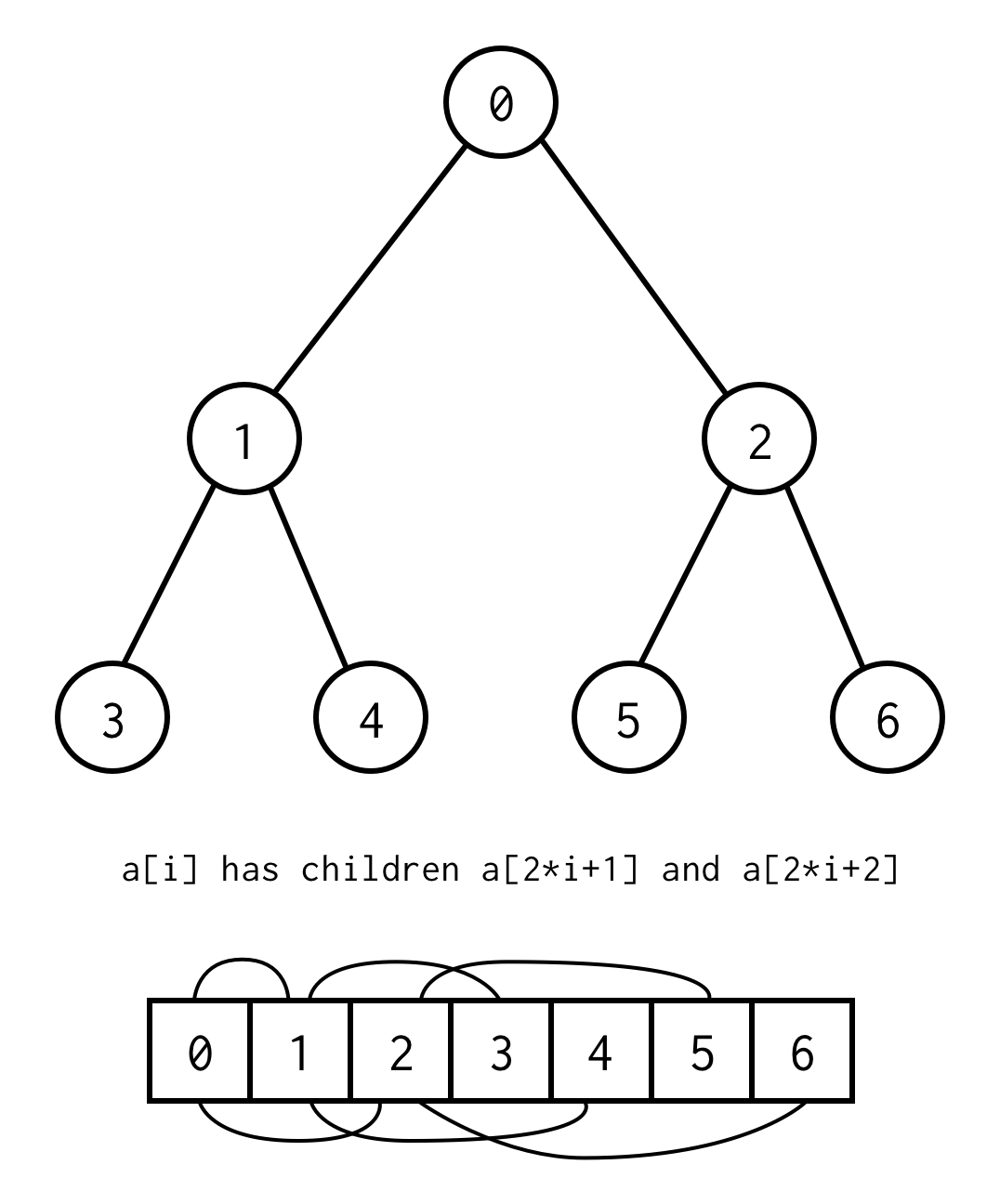
Relația dintre indicele părinte și indicele copil,ne permite să ne deplasăm de la părinte la copil, precum și de la copil la părinte

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Rețineți că arborele trebuie să fie complet, ceea ce înseamnă că pentru o anumită înălțime trebuie să conțină exact elemente.

Puteți evita această cerință plasând null în locul elementelor lipsă. enumerarea se aplică în continuare și pentru nodurile goale. Acest lucru ar trebui să acopere orice arbore binar posibil.

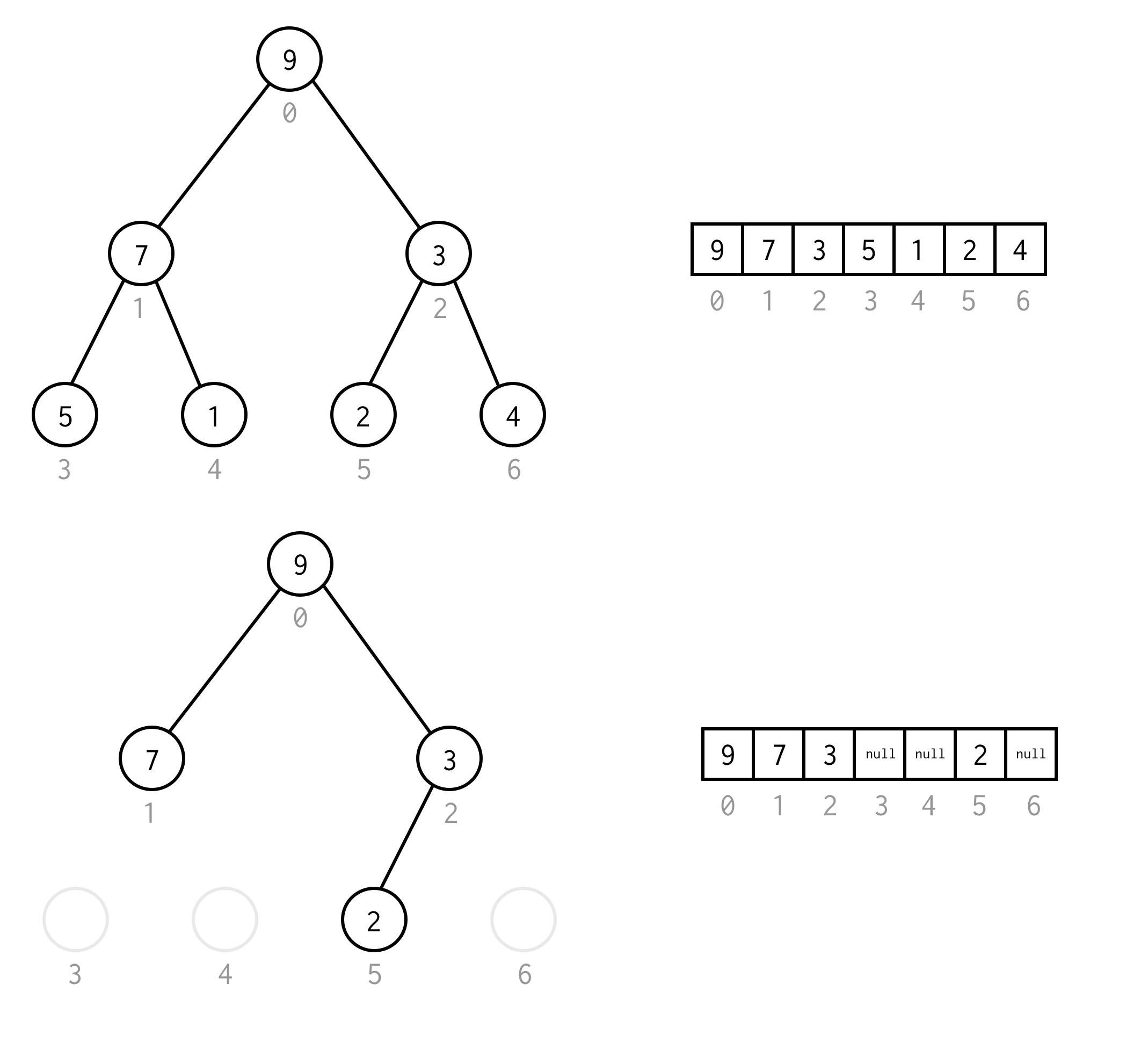
O astfel de reprezentare a matricei pentru arborele binar o vom numi Binary Tree Array.Presupunem întotdeauna că va conține elemente.

BFS vs DFS

Există doi algoritmi de căutare pentru arborele binar:breadth-first search (BFS) și depth-first search (DFS).

Cel mai bun mod de a le înțelege este vizual

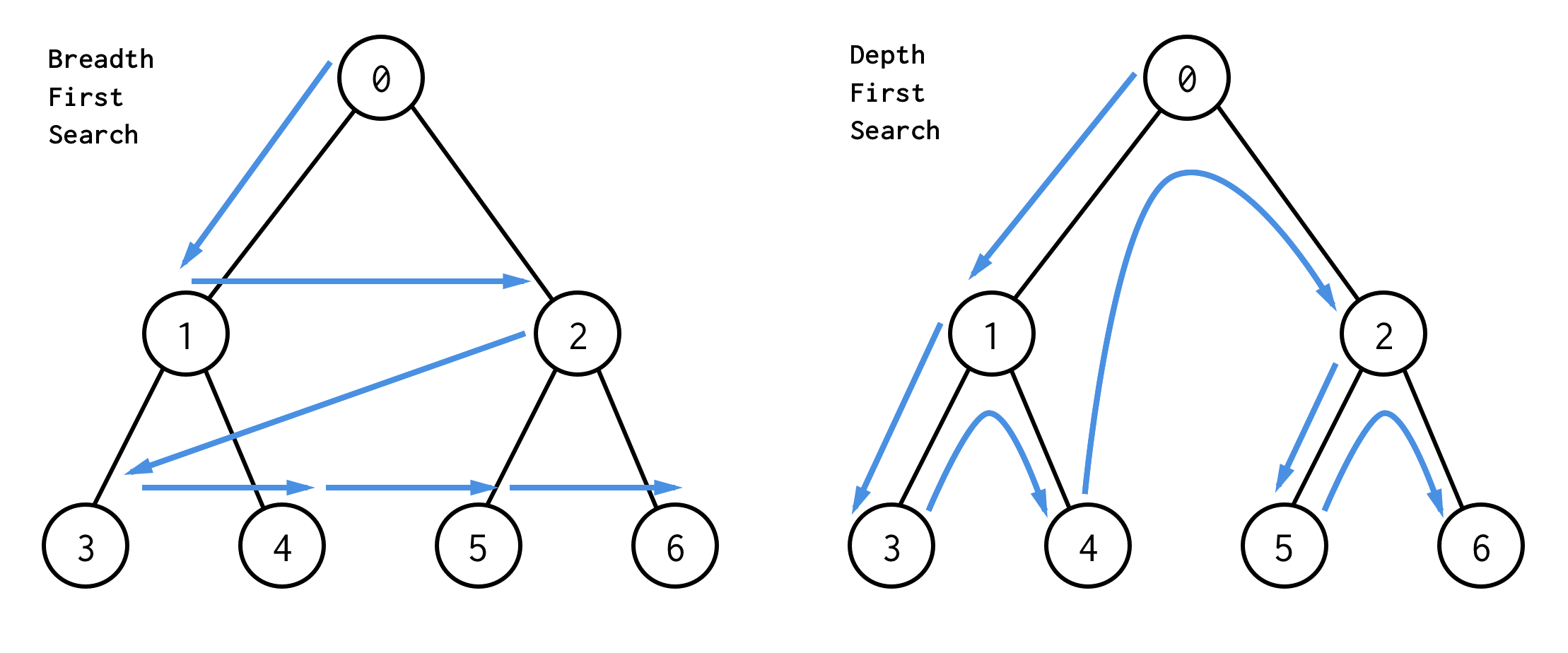
BFS caută nodurile nivel cu nivel, pornind de la nodul rădăcină. Apoi verificând copiii săi. Apoi copiii pentru copii și așa mai departe.până când toate nodurile sunt procesate sau se găsește nodul care satisface condiția de căutare.

DFS se comportă diferit. Acesta verifică toate nodurile de la calea cea mai din stânga de la rădăcină la frunză, apoi sare în sus și verifică nodul din dreapta și așa mai departe.

Pentru arborii binari clasici, BFS este implementat folosind structura de date Queue (LinkedList implementează Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Dacă înlocuiți queue cu stack veți obține implementarea DFS.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

De exemplu, să presupunem că aveți nevoie să găsiți nodul cu valoarea 1 în următorul arbore.

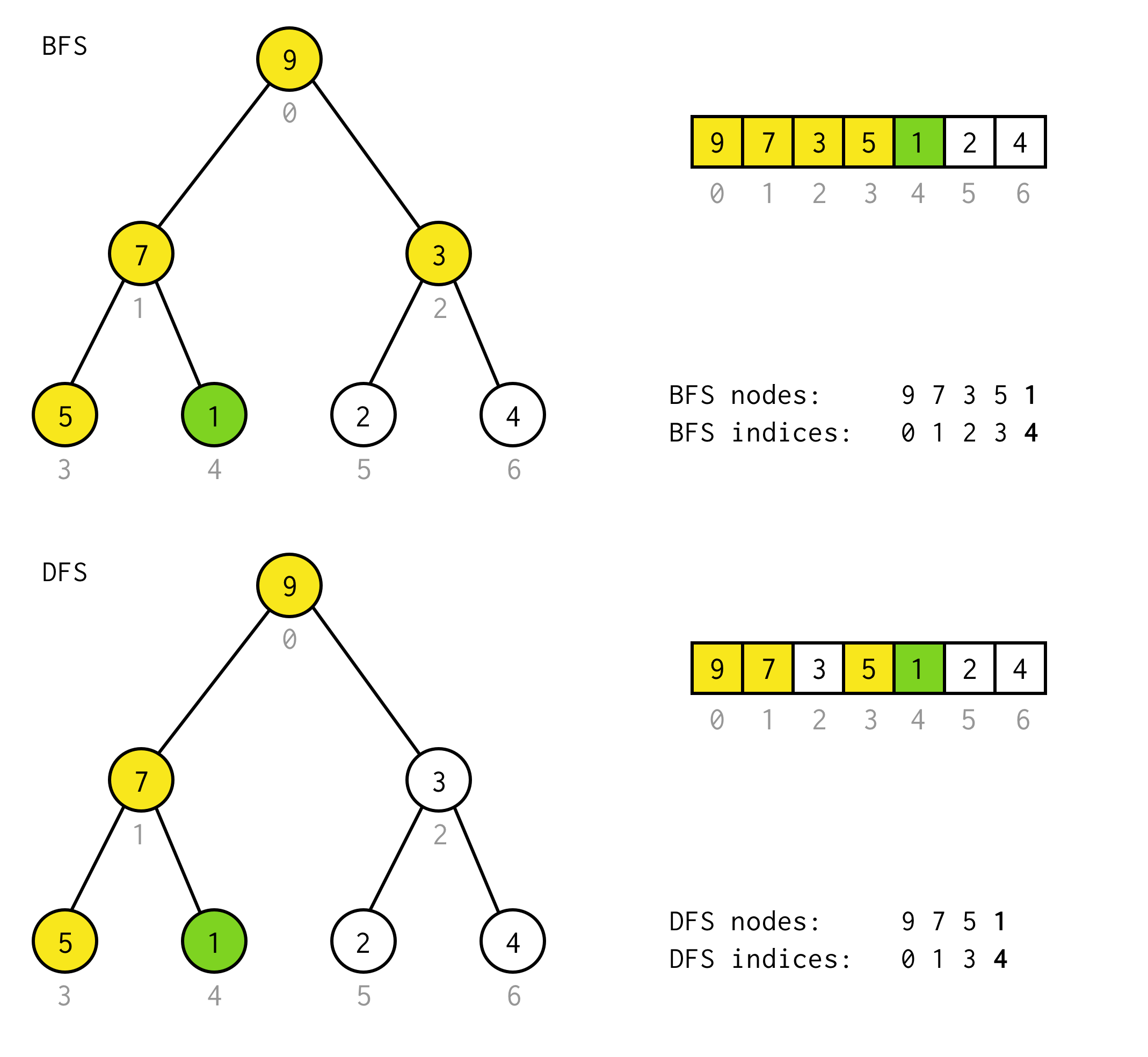
Celulele galbene sunt celule care sunt testate în algoritmul de căutare înainte ca nodul necesar să fie găsit.Luați în considerare faptul că pentru unele cazuri DFS necesită mai puține noduri pentru procesare.Pentru unele cazuri este nevoie de mai multe.

BFS și DFS pentru arborele binar

Breadth-first search pentru arborele binar este trivială.Deoarece elementele din arborele binar sunt plasate nivel cu nivel și BFS verifică, de asemenea, elementul nivel cu nivel, BFS pentru arborele binar este doar o căutare liniară

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

Depth-first search este un pic mai dificilă.

Utilizarea structurii de date stack ar putea fi implementată în același mod ca pentru arborele binar clasic, trebuie doar să puneți indicii în stack.

Din acest punct de vedere, recursivitatea nu este deloc diferită, trebuie doar să folosiți implicit stack-ul de apelare a metodei în loc de stack-ul structurii de date.

Ce-ar fi dacă am putea implementa DFS fără stivă și recursivitate.În cele din urmă este vorba doar de selectarea indicelui corect la fiecare pas?

Bine, să încercăm.

DFS for Binary Tree Array (fără stivă și recursivitate)

Ca în BFS începem de la indexul rădăcină 0.
Apoi trebuie să inspectăm copilul său din stânga, al cărui indice poate fi calculat prin formula 2*i+1.
Să numim dublarea procesului de trecere la următorul copil din stânga.

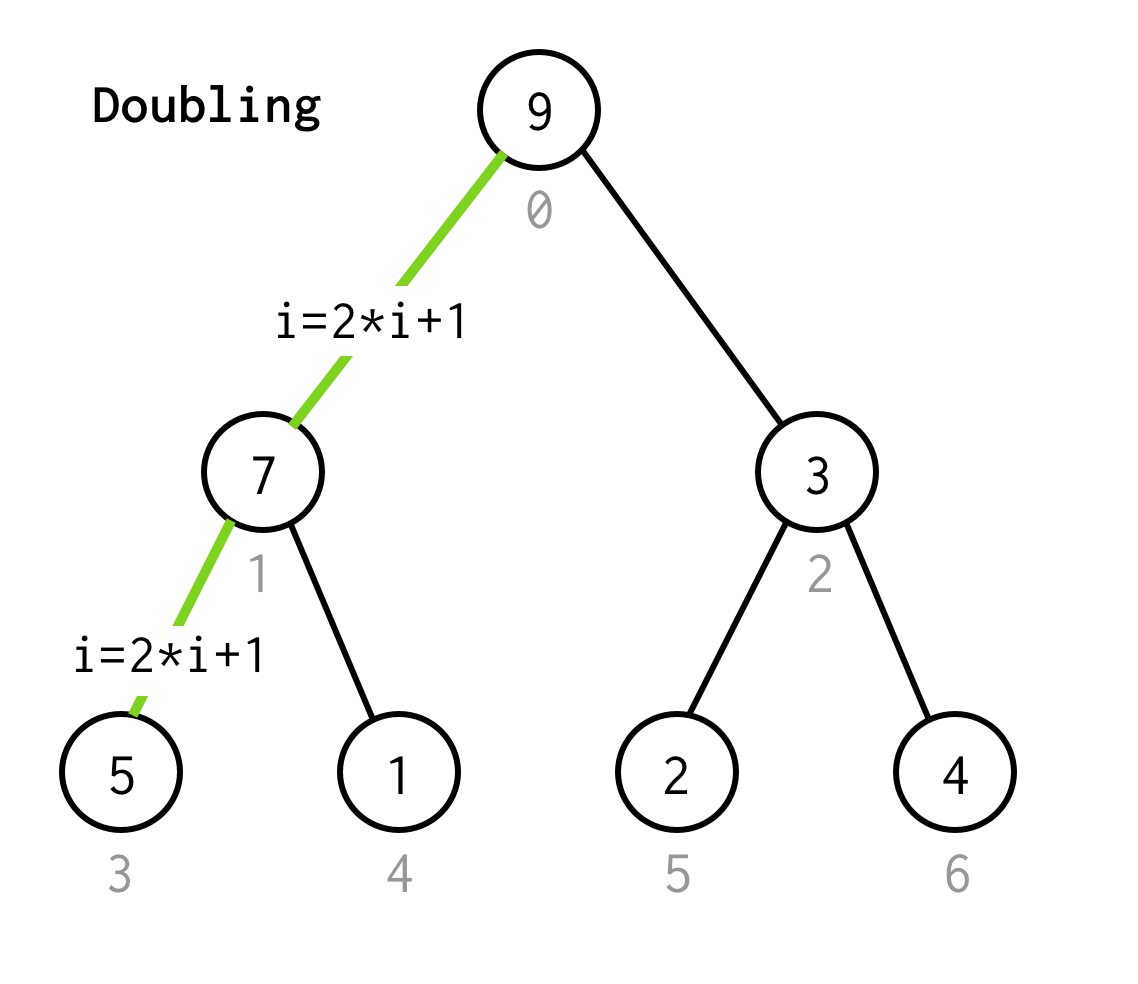
Continuăm dublarea indicelui până când nu ne oprim la nodul frunză.

Atunci cum putem înțelege că este un nod frunză?

Dacă următorul copil din stânga produce excepția index out of array bounds exceptiontrebuie să oprim dublarea și să sărim la copilul din dreapta.

Este o soluție validă, dar putem evita dublarea inutilă.Observația de aici este că numărul de elemente din arborele unor height este de două ori mai mare (și plus unu)decât arborele cu height - 1.

Pentru arborele cu height = 2 avem 7 elemente, pentru arborele cu height = 3 avem 7*2+1 = 15 elemente.

Utilizând această observație construim o condiție simplă

i < array.length / 2

Puteți verifica dacă această condiție este valabilă pentru orice nod care nu este frunză din arbore.

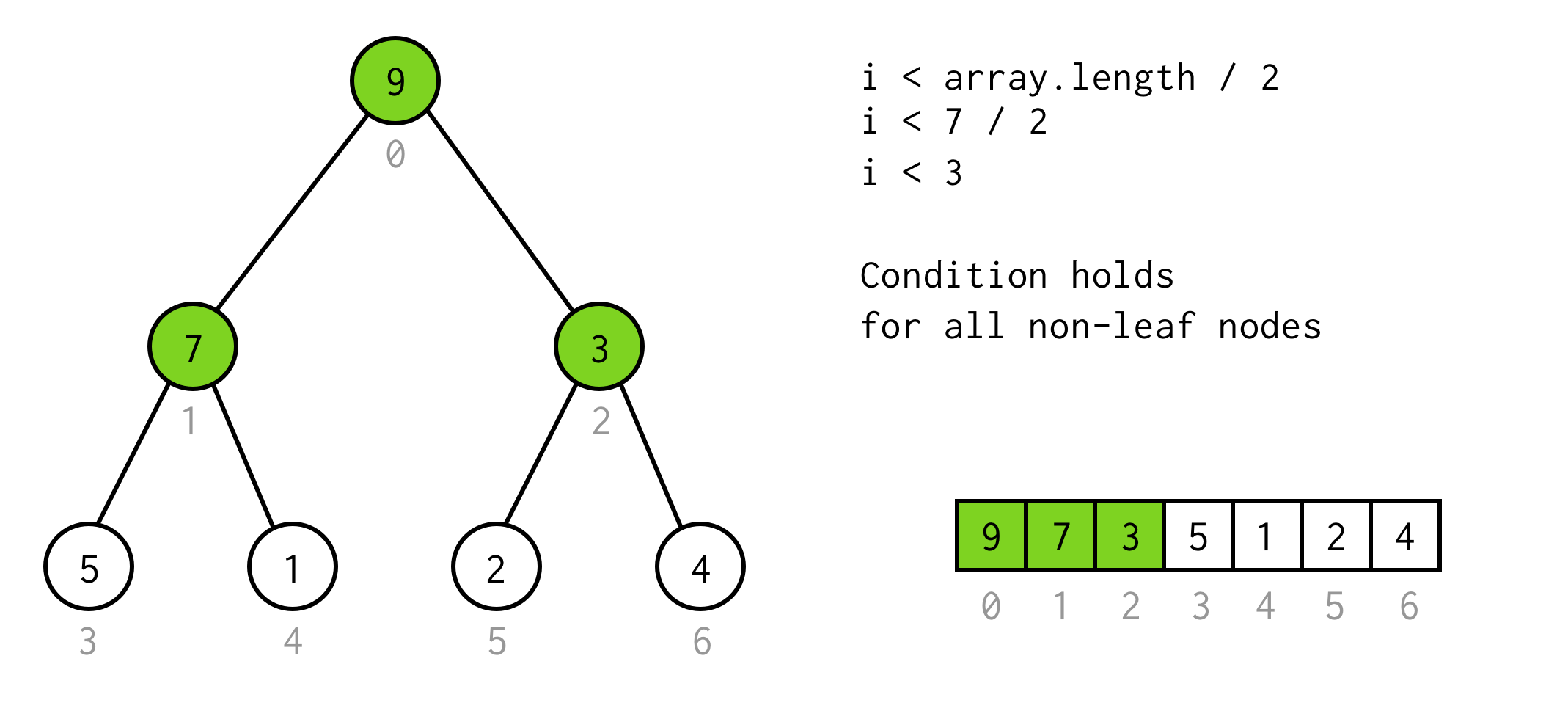
Bine până aici. Putem executa dublarea și chiar știm când să ne oprim. dar în acest fel putem verifica doar copiii din stânga nodurilor.

Când ne-am blocat la nodul frunză și nu mai putem aplica dublarea, efectuăm operația de salt.Practic, dacă dublarea este „du-te la copilul din stânga”, saltul este „du-te la părinte” și „du-te la copilul din dreapta”.

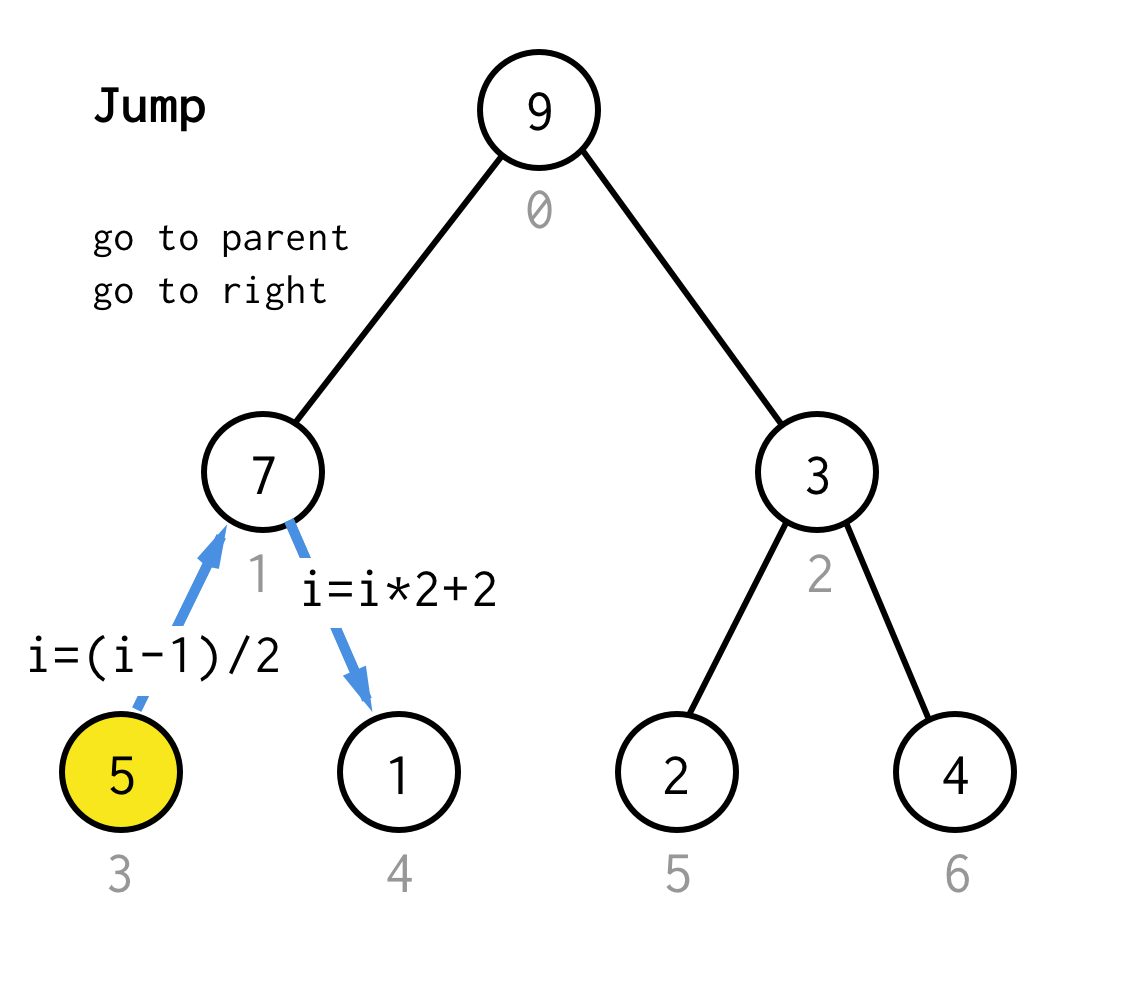
O astfel de operațiune de salt poate fi implementată prin simpla incrementare a indexului frunzei.Dar atunci când ne blocăm la următorul nod de frunză, incrementarea nu mută nodul la nodul următor, ceea ce este necesar pentru DFS.Așadar, trebuie să facem un salt dublu

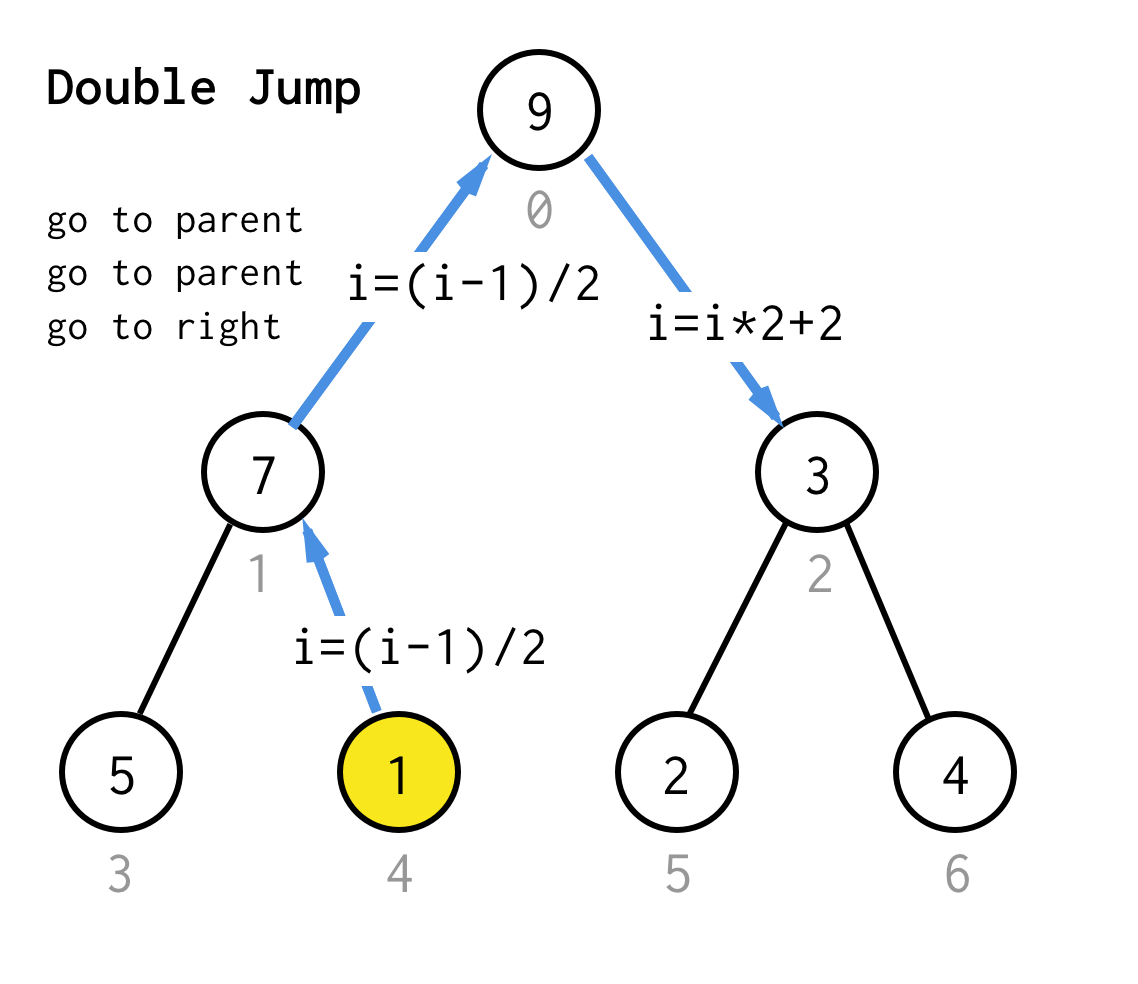
Pentru a face acest lucru mai generic, pentru algoritmul nostru am putea defini operația salt N, care specifică câte salturi la părinte sunt necesare și care se termină întotdeauna cu un salt la copilul corect.

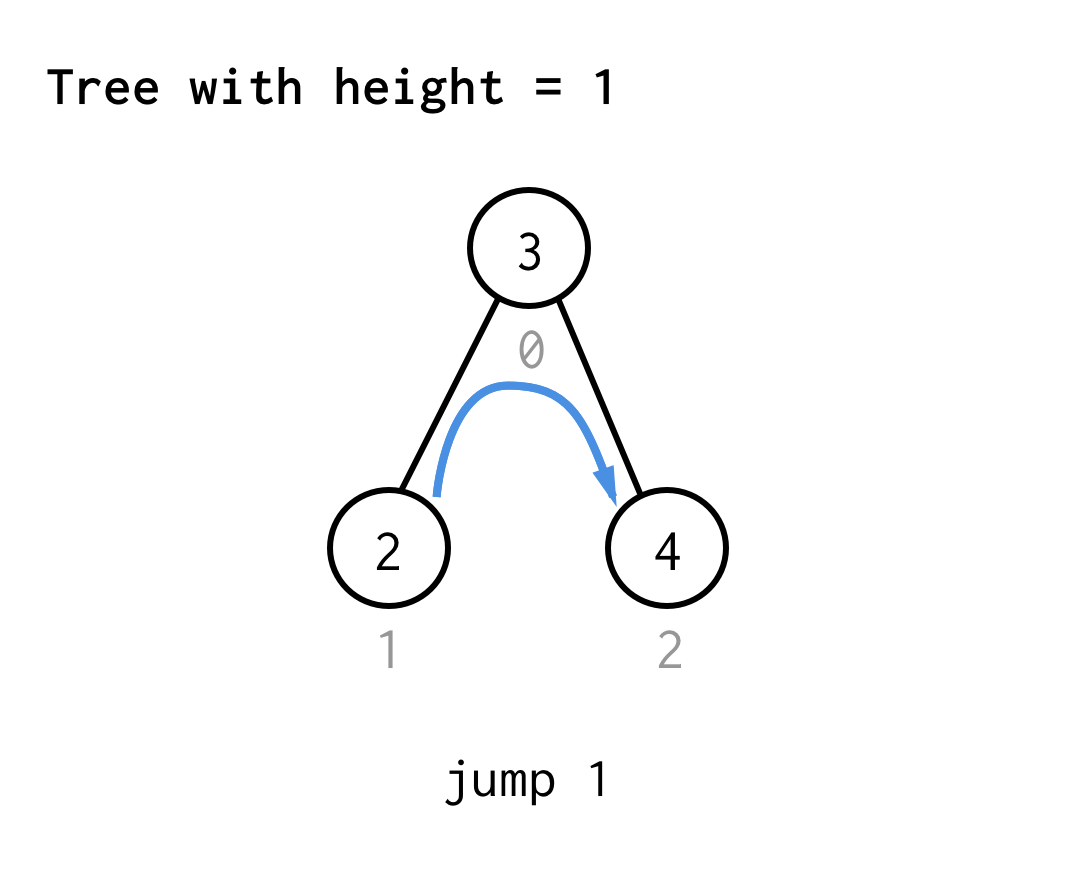
Pentru arborele cu înălțimea 1, avem nevoie de un salt, saltul 1

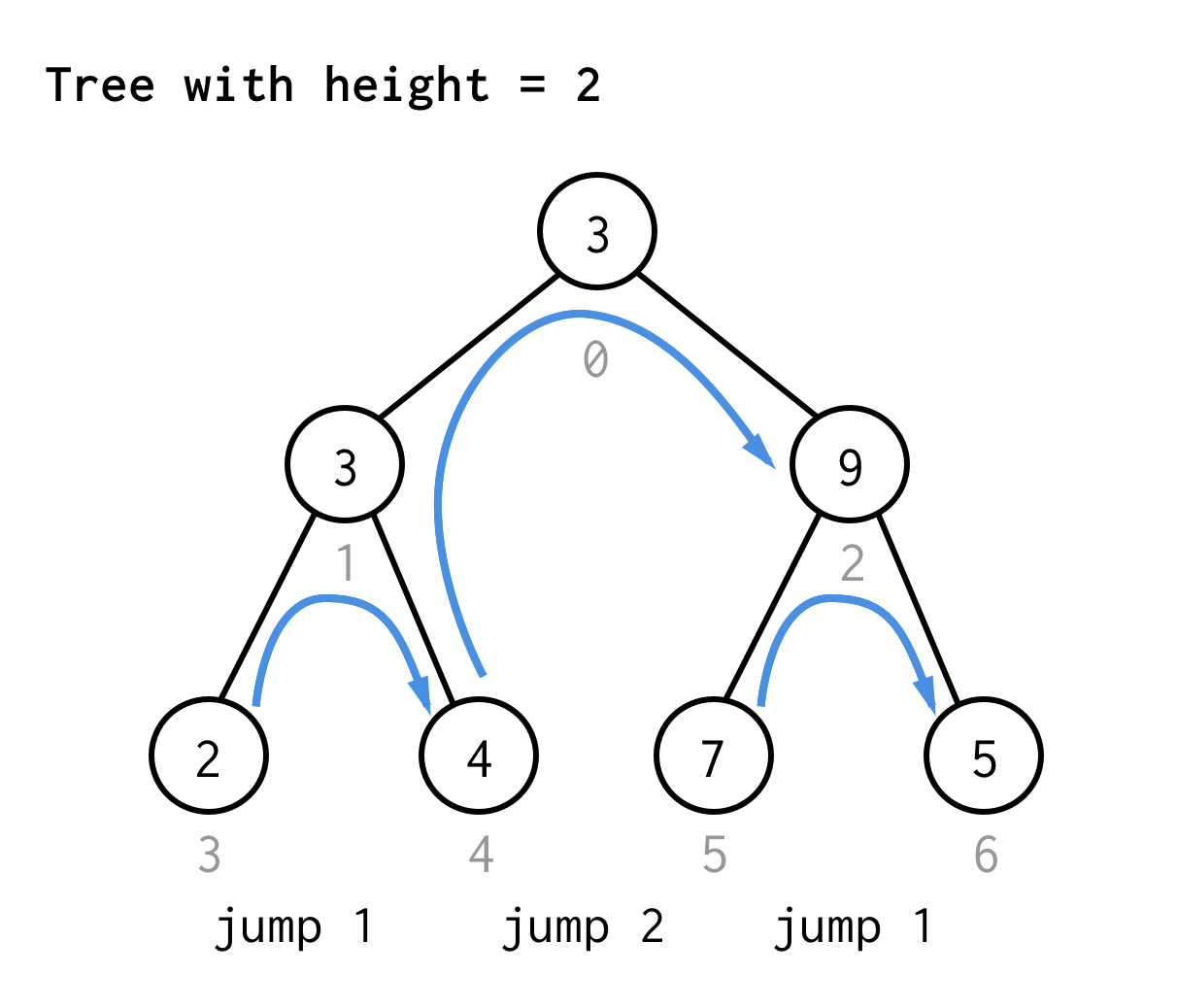
Pentru arborele cu înălțimea 2, avem nevoie de un salt, un salt dublu și apoi din nou un salt

Pentru arborele cu înălțimea 3, se pot aplica aceleași reguli și se obțin 7 salturi.

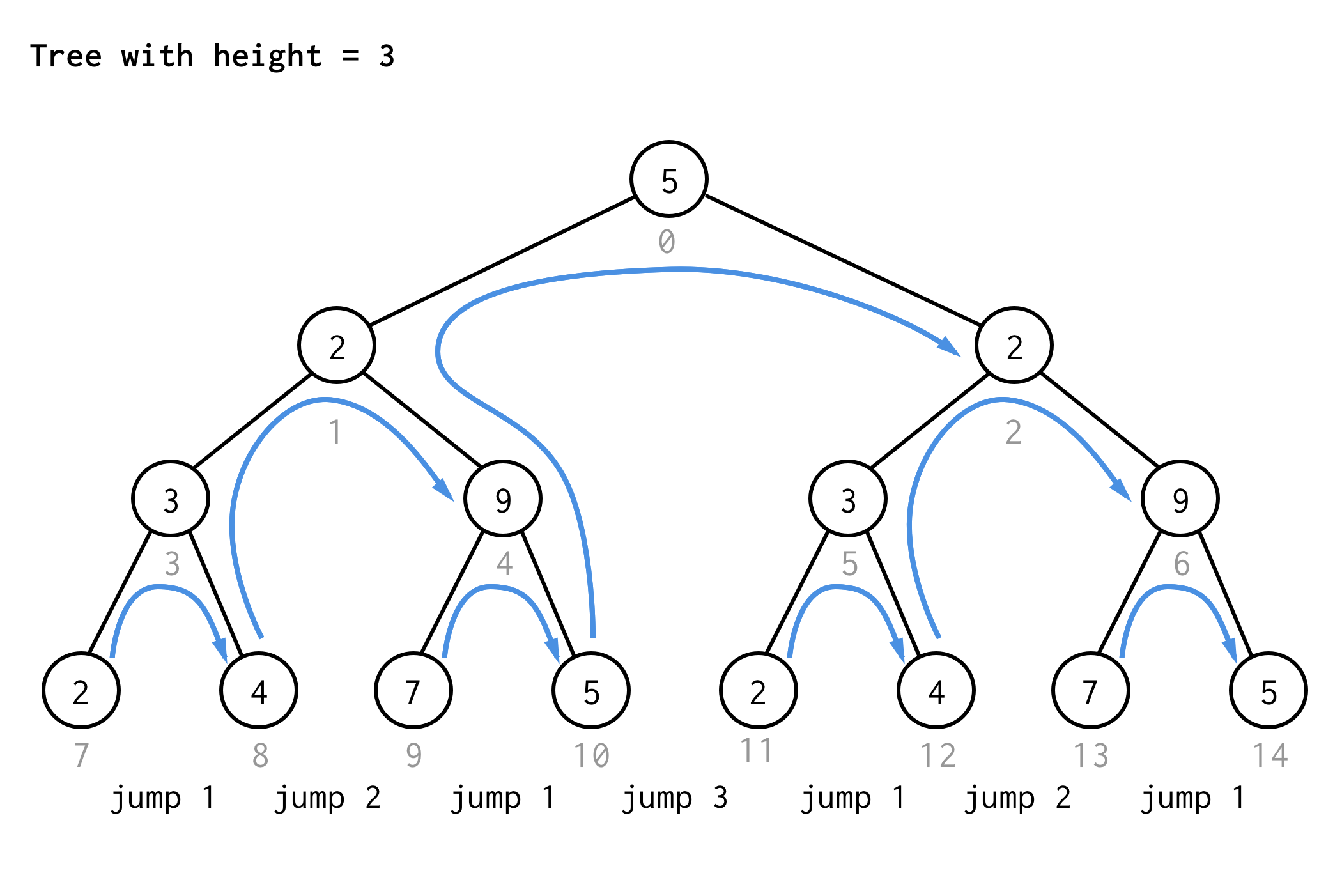
Vezi modelul?

Dacă aplicați aceeași regulă pentru arborele cu înălțimea 4 și scrieți doar valorile salturilor, veți obține următoarea secvență de numere

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Această secvență este cunoscută sub numele de cuvinte Zimin și are o definiție recursivă, ceea ce nu este grozav, deoarece nu avem voie să folosim recursivitatea.

Să găsim un alt mod de a o calcula.

Dacă vă uitați cu atenție la secvența de salt, puteți vedea un model nerecursiv.

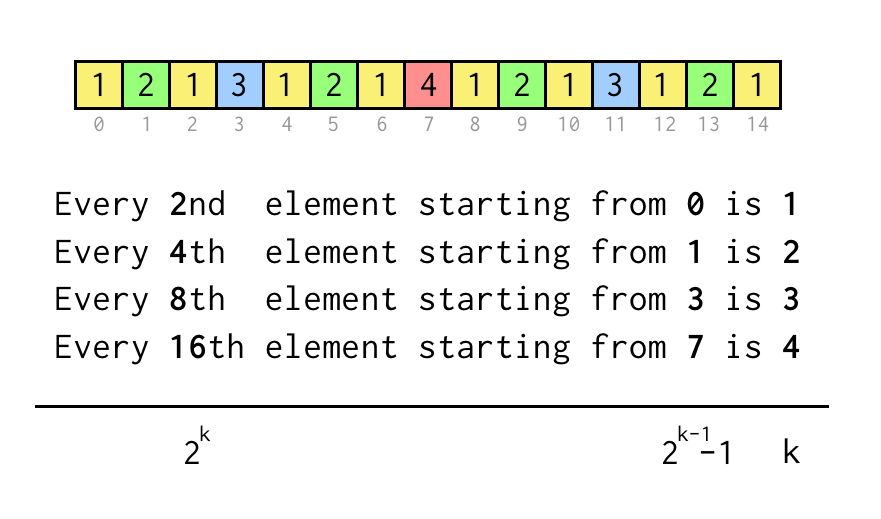
Puteți urmări indicele pentru frunza curentă j, care corespunde indicelui din matricea secvenței de mai sus.

Pentru a verifica o afirmație de genul „Fiecare al 8-lea element începând de la 3” trebuie doar să verificăm j % 8 == 3, dacă este adevărat, se fac trei salturi la nodul părinte necesar.

Procesul de salt iterativ va fi următorul

• Începeți cu k = 1
• Săriți o dată la părinte aplicând i = (i - 1)/2
• Dacă leaf % 2*k == k - 1 toate salturile au fost efectuate, ieșiți
• În caz contrar, setați k la 2*k și repetați.

Dacă puneți laolaltă tot ceea ce am discutat

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Făcut. DFS pentru matrice de arbori binari fără stivă și recursivitate

Complexitate

Complexitatea pare pătratică pentru că avem buclă în buclă,dar să vedem care este realitatea.

• Pentru jumătate din numărul total de noduri (n/2) folosim strategia de dublare, care este constantă O(1)
• Pentru cealaltă jumătate din numărul total de noduri (n/2) folosim strategia de salt de frunză.
• Jumătate din nodurile de salt de frunză (n/4) necesită doar un salt de părinte, 1 iterație. O(1)
• Jumătate din această jumătate (n/8) necesită două salturi, adică 2 iterații. O(1)
• …
• Doar un singur nod săritor de frunză necesită un salt complet la rădăcină, care este O(logN)
• Deci, dacă toate cazurile au O(1) cu excepția unuia care este O(logN), putem spune că media de salt este O(1)
• Complexitatea totală este O(n)

Performanță

Deși teoria este bună, să vedem cum funcționează acest algoritm în practică, în comparație cu altele.

Testăm 5 algoritmi, folosind JMH.

• BFS pe arbore binar (listă legată ca și coadă)
• BFS pe arbore binar Array (căutare liniară)
• DFS pe arbore binar (stivă)
• DFS on Binary Tree Array (stack)
• Iterative DFS on Binary Tree Array

Am precreat un arbore și folosim un predicat pentru a potrivi ultimul nod,pentru a ne asigura că întotdeauna atingem același număr de noduri pentru toți algoritmii.

Deci, rezultatele

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Evident, BFS pe matrice câștigă. Este doar o căutare liniară, așa că, dacă puteți reprezenta arborele binar ca matrice, faceți-o.

DFS iterativ, pe care tocmai l-am descris în articol, a ocupat locul 2și este de 4.5 ori mai lent decât căutarea liniară (BFS pe array)

Ceilalți trei algoritmi sunt chiar mai lenți decât DFS iterativ, probabil, deoarece implică structuri de date suplimentare, spațiu și alocare de memorie suplimentare.

Și cel mai rău caz este BFS pe arbore binar. Bănuiesc că aici lista legată este o problemă.

Concluzie

Binary Tree Array este un truc frumos pentru a reprezenta structura ierarhică de date ca o matrice statică (regiune contiguă în memorie). Ea definește o relație de indexare simplăpentru a trece de la părinte la copil, precum și pentru a trece de la copil la părinte, ceea ce nu este posibil cu reprezentarea clasică a matricei binare. Există unele dezavantaje, cum ar fi inserția/ștergerea lentă, dar sunt sigur că există o mulțime de aplicații pentru matricea arborescentă binară.

Așa cum am arătat, algoritmii de căutare, BFS și DFS implementați pe array-uri sunt mult mai rapizi decât frații lor pe o structură bazată pe referințe. Pentru problemele din lumea reală, acest lucru nu este atât de important și, probabil, voi folosi în continuare matricea binară bazată pe referințe.

În orice caz, a fost un exercițiu plăcut. Așteptați întrebarea „DFS on binary array without recursion and stack” la următorul interviu.

• algoritmi
• structuri de date
• programare

mishadoff 10 septembrie 2017