Wektor własny

Wektory własne to specjalny zbiór wektorów związanych z liniowym układem równań (tj.e., Równania macierzowe), które czasami są również znane jako wektory charakterystyczne, wektory właściwe lub wektory ukryte (Marcus i Minc 1988, str. 144).

Określenie wektorów własnych i wartości własnych układu jest niezwykle ważne w fizyce i inżynierii, gdzie jest równoważne diagonalizacji macierzy i pojawia się w tak powszechnych zastosowaniach jak analiza stabilności, fizyka obracających się ciał i małe oscylacje systemów wibracyjnych, aby wymienić tylko kilka. Każdemu wektorowi własnemu przyporządkowana jest odpowiadająca mu tzw. wartość własna. Z matematycznego punktu widzenia należy rozróżnić dwa różne rodzaje wektorów własnych: lewe wektory własne i prawe wektory własne. Jednak dla wielu problemów w fizyce i inżynierii wystarczy rozważać tylko prawe wektory własne. Termin „wektor własny” używany bez kwalifikacji w takich zastosowaniach można więc rozumieć jako odnoszący się do prawego wektora własnego.

Rozkład macierzy kwadratowej na wartości własne i wektory własne znany jest w tej pracy jako rozkład własny, a fakt, że rozkład ten jest zawsze możliwy, o ile macierz składająca się z wektorów własnych jest kwadratowa, znany jest jako twierdzenie o rozkładzie własnym.

Definiujemy prawy wektor własny jako wektor kolumnowy spełniający

(1)

gdzie jest macierzą, więc

(2)

co oznacza, że odpowiednie wartości własne muszą mieć wyznacznik zerowy, tzn.e.,

(3)

Podobnie, zdefiniuj lewy wektor własny jako wektor rzędowy spełniający

(4)

Przyjęcie transpozycji każdej ze stron daje

(5)

którą można przepisać jako

(6)

Przestudiuj ponownie, aby otrzymać

(7)

co oznacza

(8)

Przepisanie daje

0=det(A^(T)-lambda_LI)		det(A^(T)-lambda_LI^(T)-lambda_LI)		.lambda_LI^(T))	(9)
			(10)
			(11)

gdzie ostatni krok wynika z tożsamości

(12)

Zrównanie równań (◇) i (11), które oba są równe 0 dla dowolnych i , wymaga zatem, aby , tzn, lewa i prawa wartość własna są równoważne, co nie jest prawdą dla wektorów własnych.

Niech będzie macierzą utworzoną przez kolumny prawych wektorów własnych, a będzie macierzą utworzoną przez wiersze lewych wektorów własnych. Niech

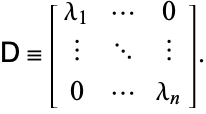(13)

Then

.

.

			(14)
			(15)

i

.

			(16)
			(17)

so

(18)

Ale to równanie ma postać

.

(19)

gdzie jest macierzą diagonalną, więc musi być prawdą, że jest również diagonalna. W szczególności, jeśli jest macierzą symetryczną, to lewy i prawy wektor własny są po prostu wzajemnymi transpozycjami, a jeśli jest macierzą samoprzylepną (tzn. jest hermitowska), to lewy i prawy wektor własny są macierzami addytywnymi.

Wektory własne nie mogą być równe wektorowi zerowemu. Niezerowa skalarna wielokrotność wektora własnego jest równoważna oryginalnemu wektorowi własnemu. Stąd, bez utraty ogólności, wektory własne są często normalizowane do jednostki długości.

While an matrix always has eigenvalues, some or all of which may be degenerate, such a matrix may have between 0 and linearly independent eigenvectors. Na przykład, macierz ma tylko pojedynczy wektor własny .

Wektory własne mogą być obliczane w Wolfram Language za pomocą Eigenvectors. To polecenie zawsze zwraca listę o długości , więc wszelkie wektory własne, które nie są liniowo niezależne są zwracane jako wektory zerowe. Wektory własne i wartości własne mogą być zwrócone razem za pomocą polecenia Eigensystem.

Dana jest macierz z wektorami własnymi , i oraz odpowiadającymi im wartościami własnymi , , i , to dowolny wektor można zapisać

(20)

Zastosowanie macierzy ,

.

			(21)
			(22)

so

(23)

Jeśli , oraz , wynika stąd, że

(24)

tak więc wielokrotne przyłożenie macierzy do dowolnego wektora zdumiewająco daje wektor proporcjonalny do wektora własnego o największej wartości własnej.