Privacy & Cookies
Ta strona używa plików cookies. Kontynuując, wyrażasz zgodę na ich użycie. Dowiedz się więcej, w tym jak kontrolować pliki cookie.
Spirala to krzywa, która „emanuje z punktu, oddalając się w miarę jak obraca się wokół punktu”.

Istnieje wiele różnych rodzajów spiral w zależności od wzorów, które je tworzą. W tym wpisie na blogu omówię spirale dwuwymiarowe (zauważ, że istnieje również wiele różnych spirali trójwymiarowych).
Spirala Archimedesa
Jest to spirala nazwana na cześć słynnego greckiego matematyka Archimedesa, który jako pierwszy opisał ją w swojej książce O spiralach. Opisuje ją następujące równanie biegunowe:
gdzie a i b są liczbami rzeczywistymi.
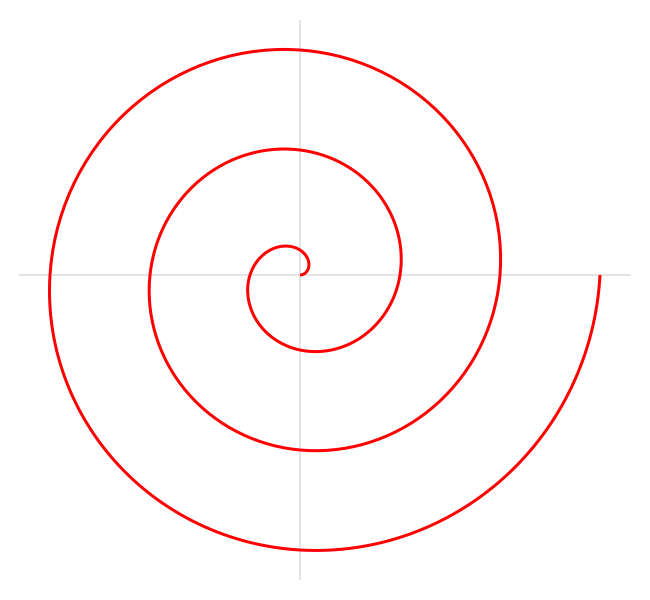
Zmieniając parametr a spirala będzie się obracać, a parametr b kontroluje odległość między kolejnymi obrotami.
Spirala Fermata
Spirala Fermata jest spiralą paraboliczną, która spełnia następujące równanie biegunowe:
Jest to rodzaj spirali Archimedesa.

Spirala Eulera
Znana również jako spirala Cornu, jest to krzywa, której krzywizna rośnie wraz ze wzrostem odległości od początku; „krzywizna krzywej kołowej jest równa odwrotności promienia”.

Forma parametrowa składa się z dwóch równań z przedziałami Fresnela, które można rozwiązać tylko w przybliżeniu.
Całości te, a tym samym spirala Eulera, mogą być użyte do opisu rozkładu energii dyfrakcji Fresnela na pojedynczej szczelinie w teorii falowej.
Spirala hiperboliczna
Pomyślana po raz pierwszy przez Pierre’a Varignona w 1704 roku, spirala hiperboliczna jest krzywą transcendentalną, co oznacza, że „jest funkcją analityczną, która nie spełnia równania wielomianowego”. Jest przeciwieństwem spirali Archimedesa i dlatego ma następujące równanie biegunowe:
W środku znajduje się w nieskończonej odległości od bieguna; dla θ zaczynającego się od 0, r zaczyna się w nieskończoności.
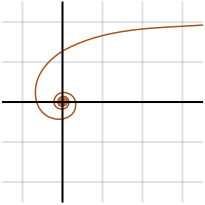
Lituus
Lituus jest spiralą o równaniu biegunowym:
gdzie k jest stałą. Stąd kąt jest odwrotnie proporcjonalny do kwadratu promienia. 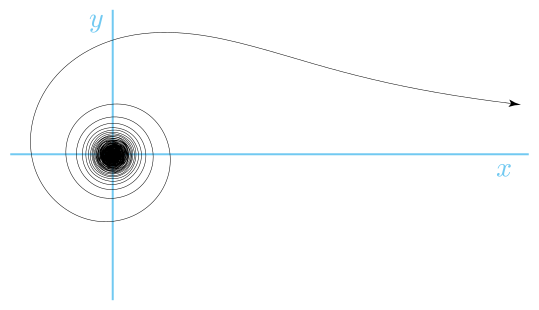
Krzywa ta została nazwana na cześć starożytnego rzymskiego lituus (zakrzywiona laska wróżebna lub trąbka wojenna) przez Rogera Cotes’a w zbiorze prac opublikowanych w 1722 roku.
Spirala logarytmiczna
 Spirala logarytmiczna jest samopodobną spiralą, która często występuje w przyrodzie. Po raz pierwszy została opisana przez Kartezjusza, ale dogłębnie zbadał ją Jacob Bernoulli, który nazwał ją „cudowną spiralą”. Ma ona biegunowe równania
Spirala logarytmiczna jest samopodobną spiralą, która często występuje w przyrodzie. Po raz pierwszy została opisana przez Kartezjusza, ale dogłębnie zbadał ją Jacob Bernoulli, który nazwał ją „cudowną spiralą”. Ma ona biegunowe równania
.





Dodaj komentarz