mishadoff thoughts

Implementing Depth-First Search for the Binary Tree without stack and recursion.

Binary Tree Array

This is binary tree.

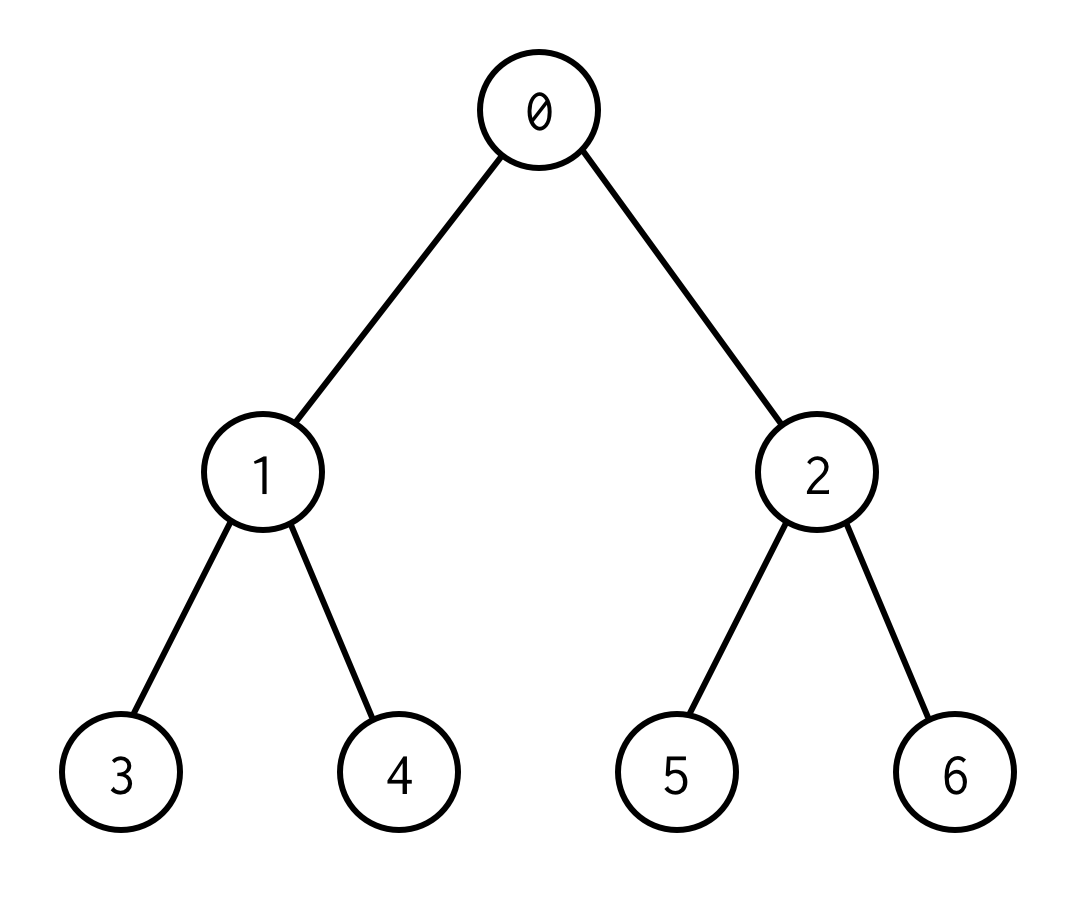
0 is a root node.
0 has two children: left 1 and right: 2.
Każde z jego dzieci ma swoje dzieci i tak dalej.
Węzły bez dzieci to węzły liści (3,4,5,6).

Liczba krawędzi między węzłami korzenia i liści definiuje wysokość drzewa.Powyższe drzewo ma wysokość 2.

Standardowym podejściem do implementacji drzewa binarnego jest zdefiniowanie klasy o nazwie BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Jednakże istnieje sztuczka pozwalająca zaimplementować drzewo binarne używając tylko statycznych tablic.Jeśli wyliczymy wszystkie węzły w drzewie binarnym według poziomów zaczynając od zera, możemy to spakować do tablicy.

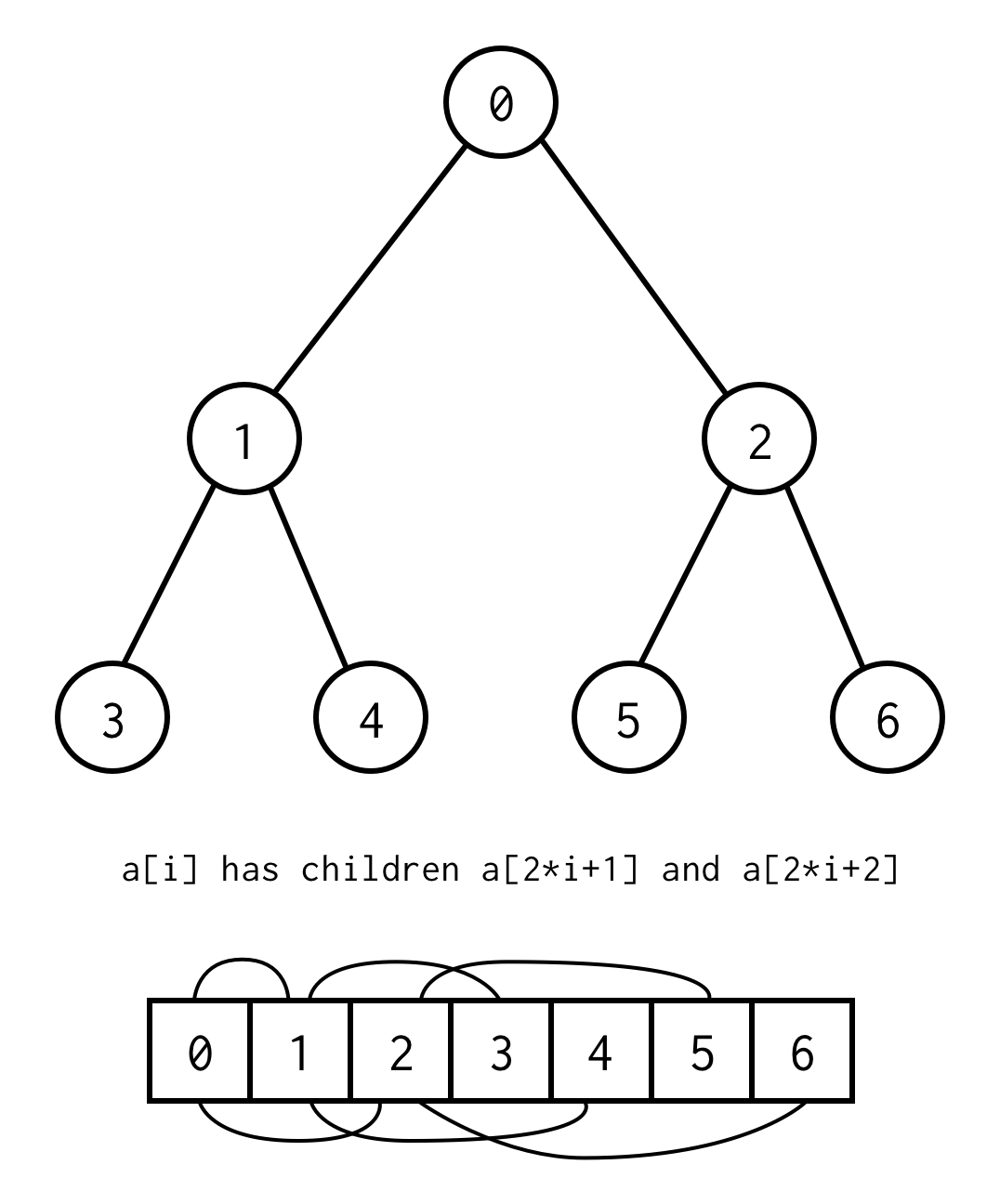
Zależność między indeksem rodzica a indeksem dziecka, pozwala nam na przechodzenie od rodzica do dziecka, jak również od dziecka do rodzica

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Ważna uwaga, że drzewo powinno być kompletne, co oznacza, że dla określonej wysokości powinno zawierać dokładnie elementy.

Możesz uniknąć tego wymogu umieszczając null zamiast brakujących elementów.Wyliczenie nadal dotyczy również pustych węzłów. To powinno pokryć każde możliwe drzewo binarne.

Taką reprezentację tablicową dla drzewa binarnego będziemy nazywać Binary Tree Array.Zawsze zakładamy, że będzie ona zawierała elementy.

BFS vs DFS

Dla drzewa binarnego istnieją dwa algorytmy wyszukiwania:breadth-first search (BFS) i depth-first search (DFS).

Najlepszym sposobem na ich zrozumienie jest wizualne

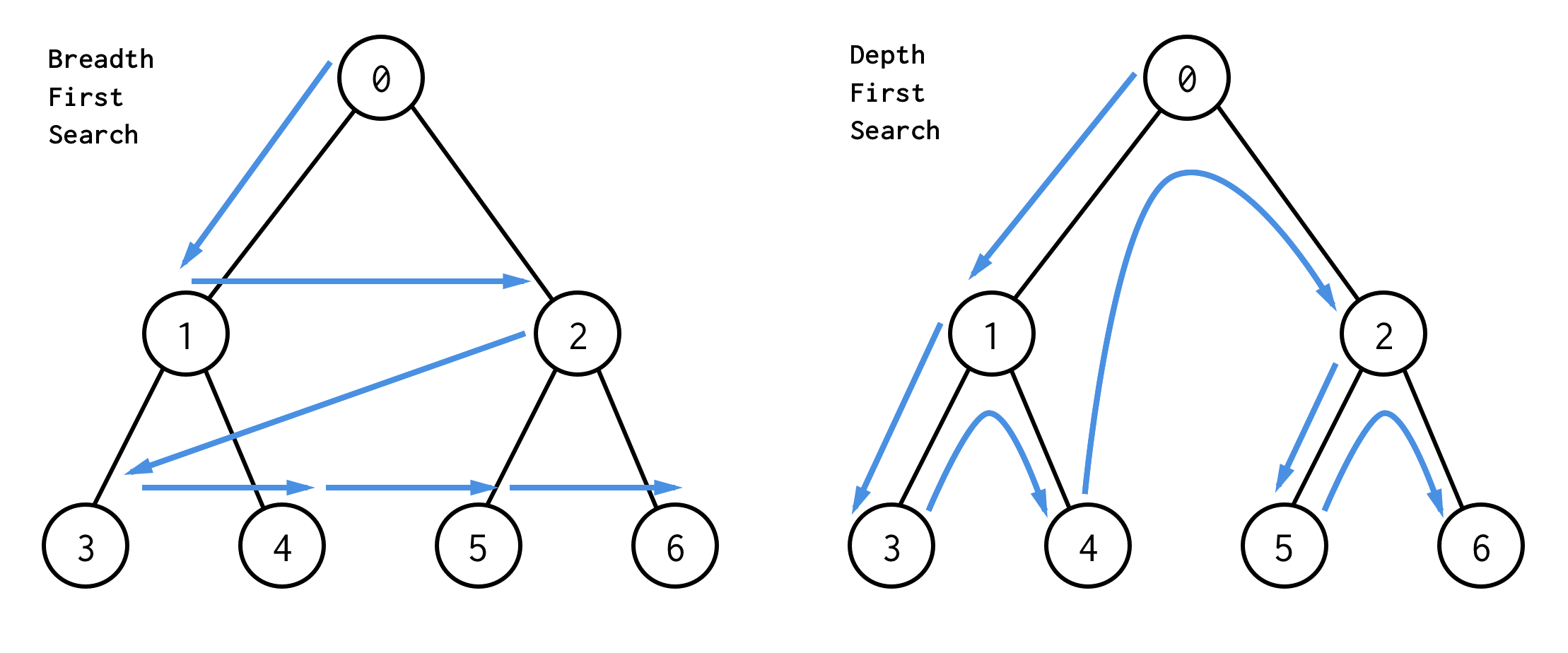
BFS przeszukuje węzły poziom po poziomie, zaczynając od węzła głównego. Następnie sprawdzając jego dzieci. Następnie dzieci dla dzieci i tak dalej, aż wszystkie węzły zostaną przetworzone lub zostanie znaleziony węzeł, który spełnia warunek wyszukiwania.

DFS zachowuje się inaczej. Sprawdza wszystkie węzły od najbardziej lewej ścieżki od korzenia do liścia, następnie przeskakuje w górę i sprawdza prawy węzeł i tak dalej.

Dla klasycznych drzew binarnych BFS zaimplementowany przy użyciu struktury danych Queue (LinkedList implementuje Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Jeśli zastąpisz kolejkę stosem otrzymasz implementację DFS.

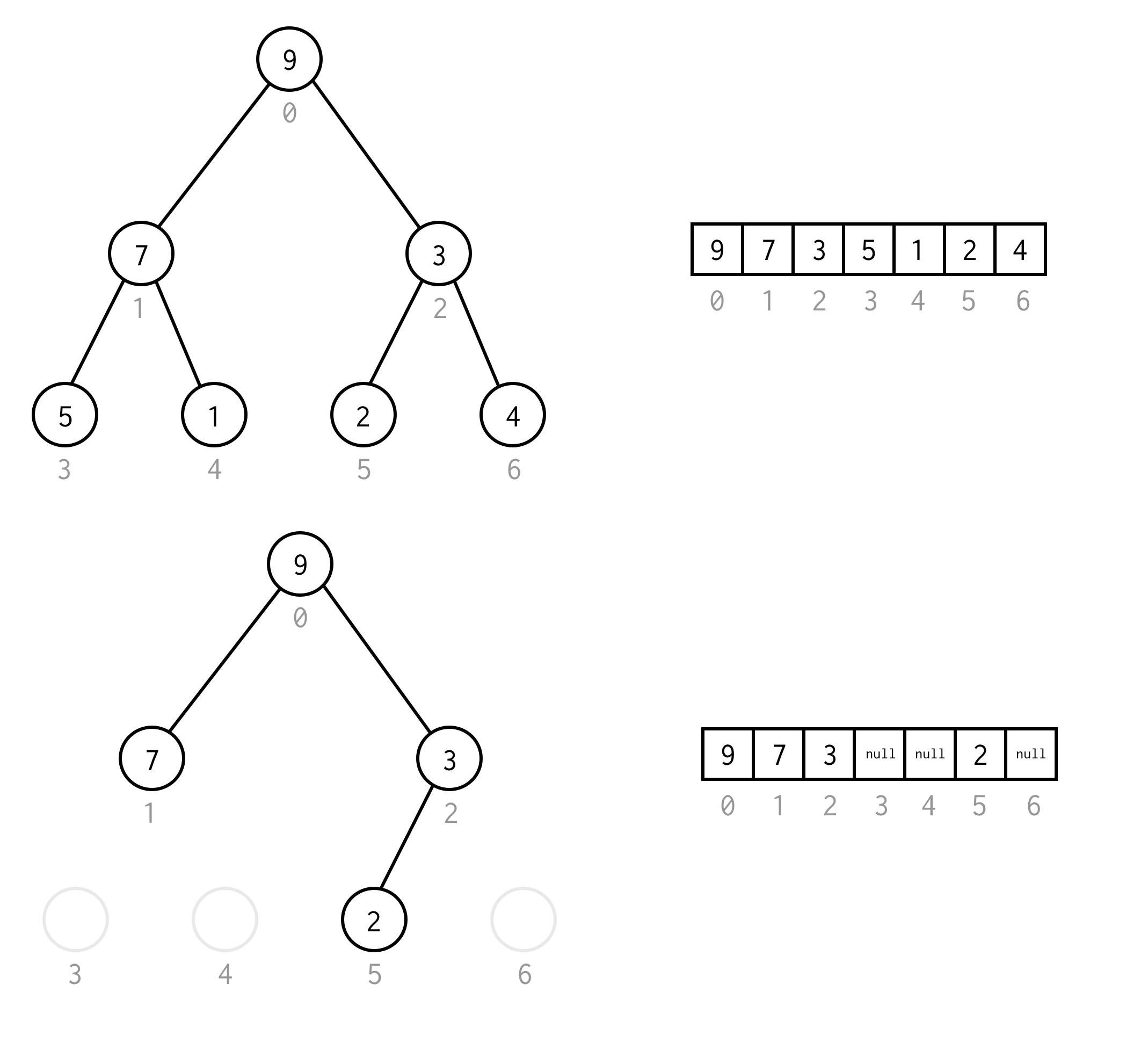
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Na przykład, załóżmy, że musisz znaleźć węzeł o wartości 1 w następującym drzewie.

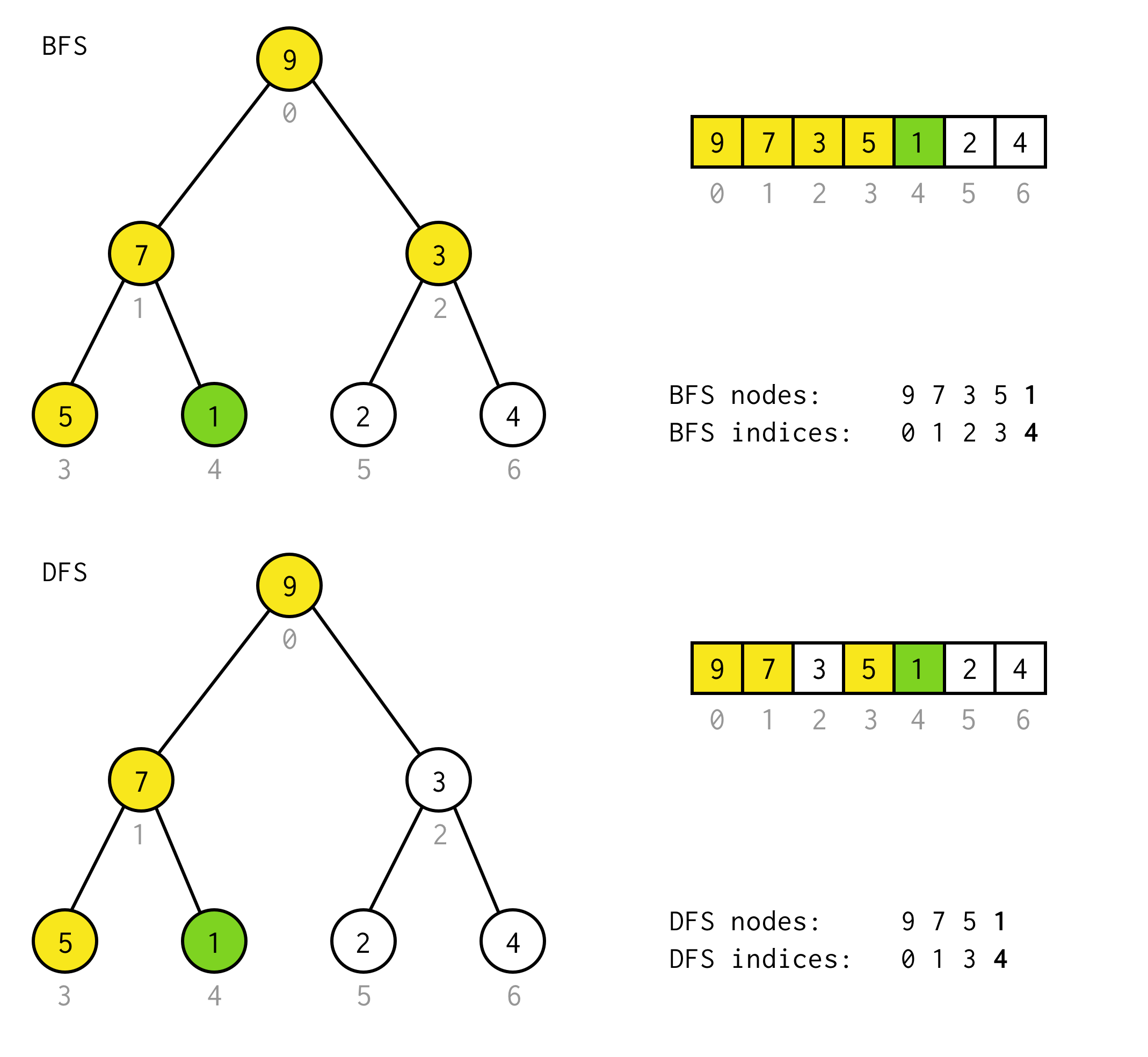
Żółte komórki są komórkami, które są testowane w algorytmie wyszukiwania przed znalezieniem potrzebnego węzła.Weź pod uwagę, że w niektórych przypadkach DFS wymaga mniej węzłów do przetwarzania.Dla niektórych przypadków wymaga więcej.

BFS i DFS dla tablicy drzew binarnych

Szukanie w pierwszym rzędzie dla tablicy drzew binarnych jest trywialne.Ponieważ elementy w tablicy drzew binarnych są umieszczane poziom po poziomie ibfs również sprawdza element poziom po poziomie, bfs dla tablicy drzew binarnych jest po prostu szukaniem liniowym

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

Szukanie wgłąb jest nieco trudniejsze.

Używając struktury danych stosu, można to zaimplementować w taki sam sposób, jak w przypadku klasycznego drzewa binarnego, wystarczy umieścić indeksy na stosie.

Od tego momentu rekurencja nie różni się w ogóle, po prostu używasz stosu wywołania metody implicit zamiast stosu struktury danych.

A co jeśli moglibyśmy zaimplementować DFS bez stosu i rekurencji.W końcu to tylko wybieranie poprawnego indeksu na każdym kroku?

Dobrze, spróbujmy.

DFS dla Binary Tree Array (bez stosu i rekurencji)

Jak w BFS zaczynamy od indeksu korzenia 0.
Następnie musimy sprawdzić jego lewe dziecko, którego indeks można obliczyć za pomocą wzoru 2*i+1.
Proces przechodzenia do następnego lewego dziecka nazwijmy podwajaniem.

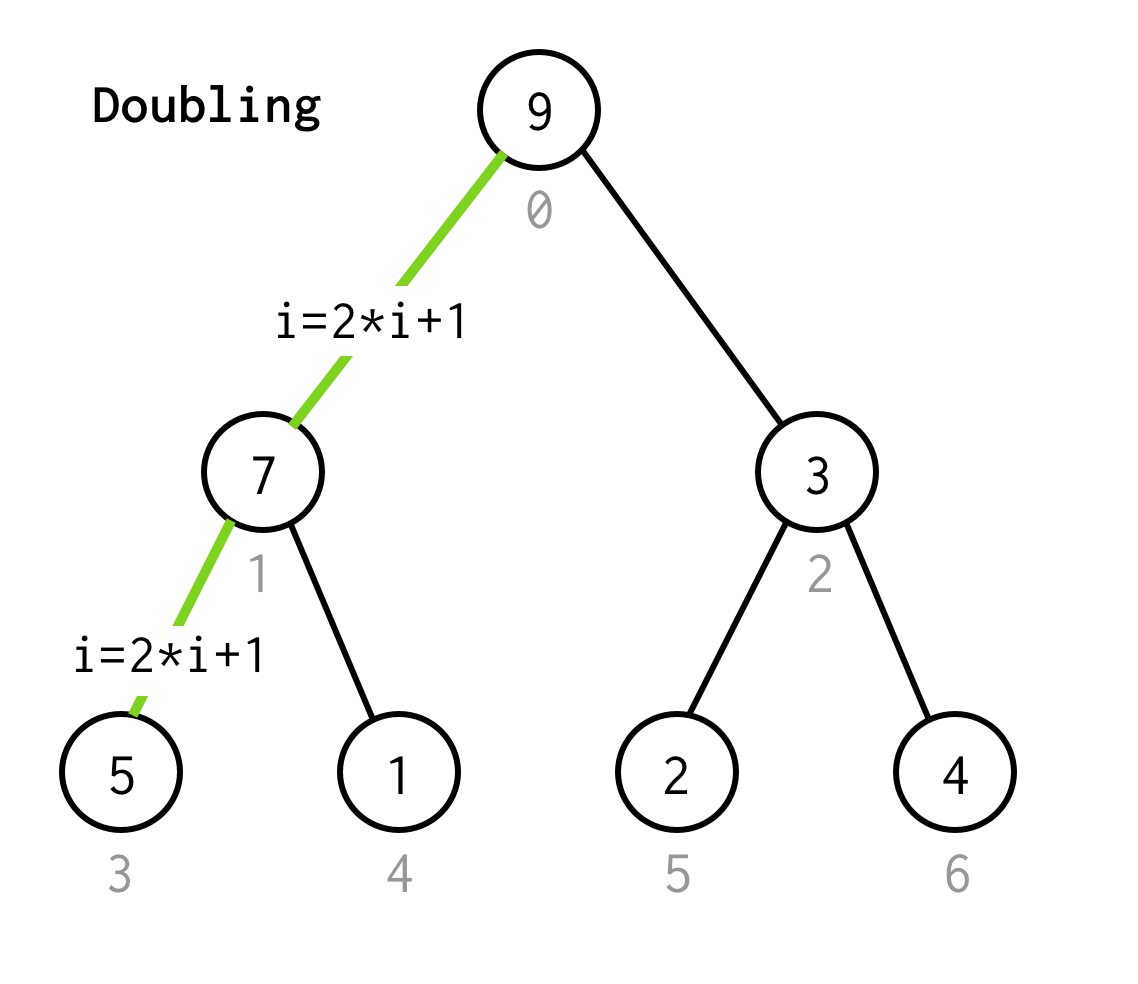
Kontynuujemy podwajanie indeksu, aż nie zatrzymamy się na węźle liścia.

Więc jak możemy zrozumieć, że jest to węzeł liścia?

If next left child produce index out of array bounds exceptionwe need to stop doubling and jump to the right child.

That’s a valid solution, but we can avoid unnesessary doubling.The observation here is the number of elements in the tree of some height is two times larger (and plus one)than the tree with height - 1.

Dla drzewa z height = 2 mamy 7 elementów, dla drzewa z height = 3 mamy 7*2+1 = 15 elementów.

Korzystając z tej obserwacji budujemy prosty warunek

i < array.length / 2

Można sprawdzić, że ten warunek jest ważny dla dowolnego węzła nie-liścia w drzewie.

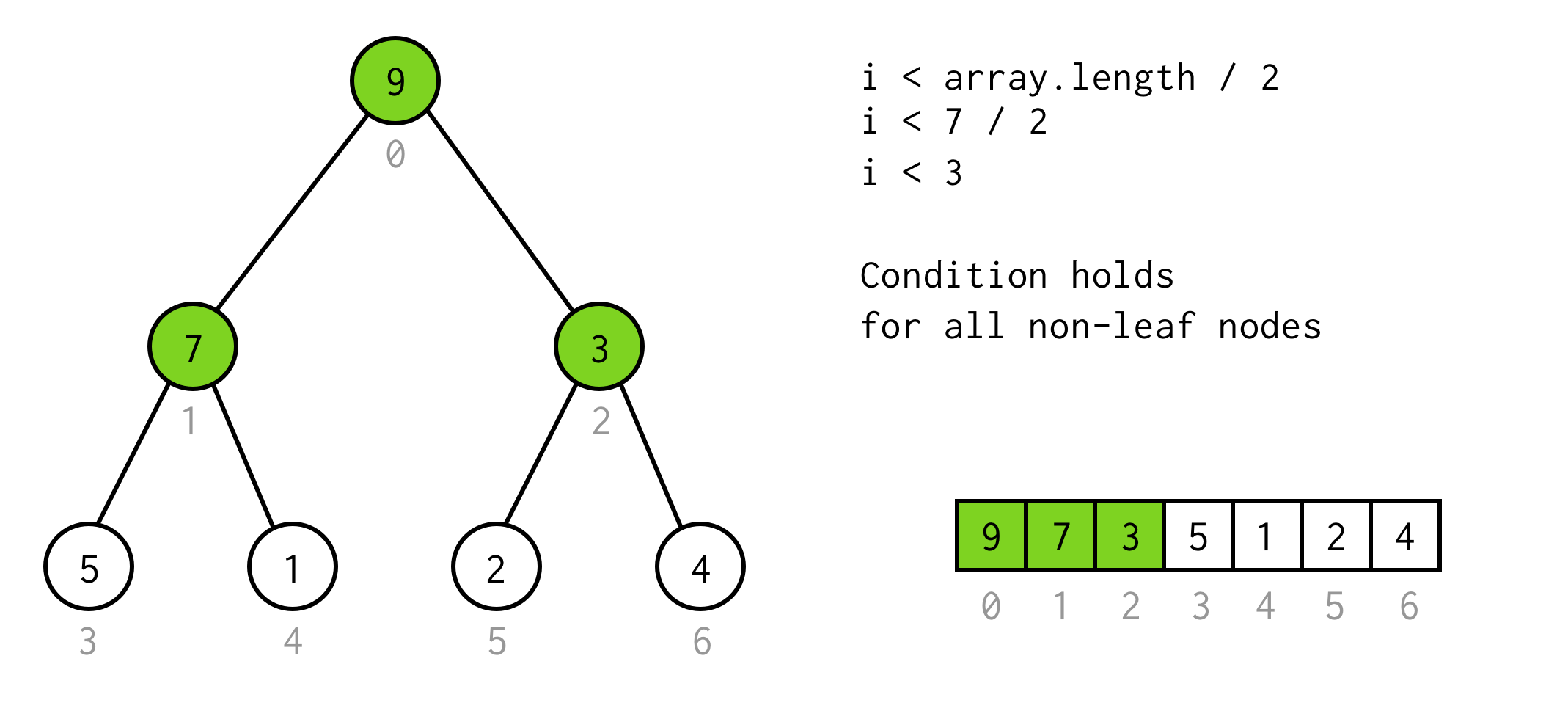
Jak na razie jest ładnie. Możemy uruchomić podwajanie, a nawet wiemy, kiedy się zatrzymać.Ale w ten sposób możemy sprawdzić tylko lewe dzieci węzłów.

Gdy utknęliśmy w węźle liścia i nie możemy już zastosować podwajania, wykonujemy operację skoku.Zasadniczo, jeśli podwajanie jest pójściem do lewego dziecka, skok jest pójściem do rodzica i pójściem do prawego dziecka.

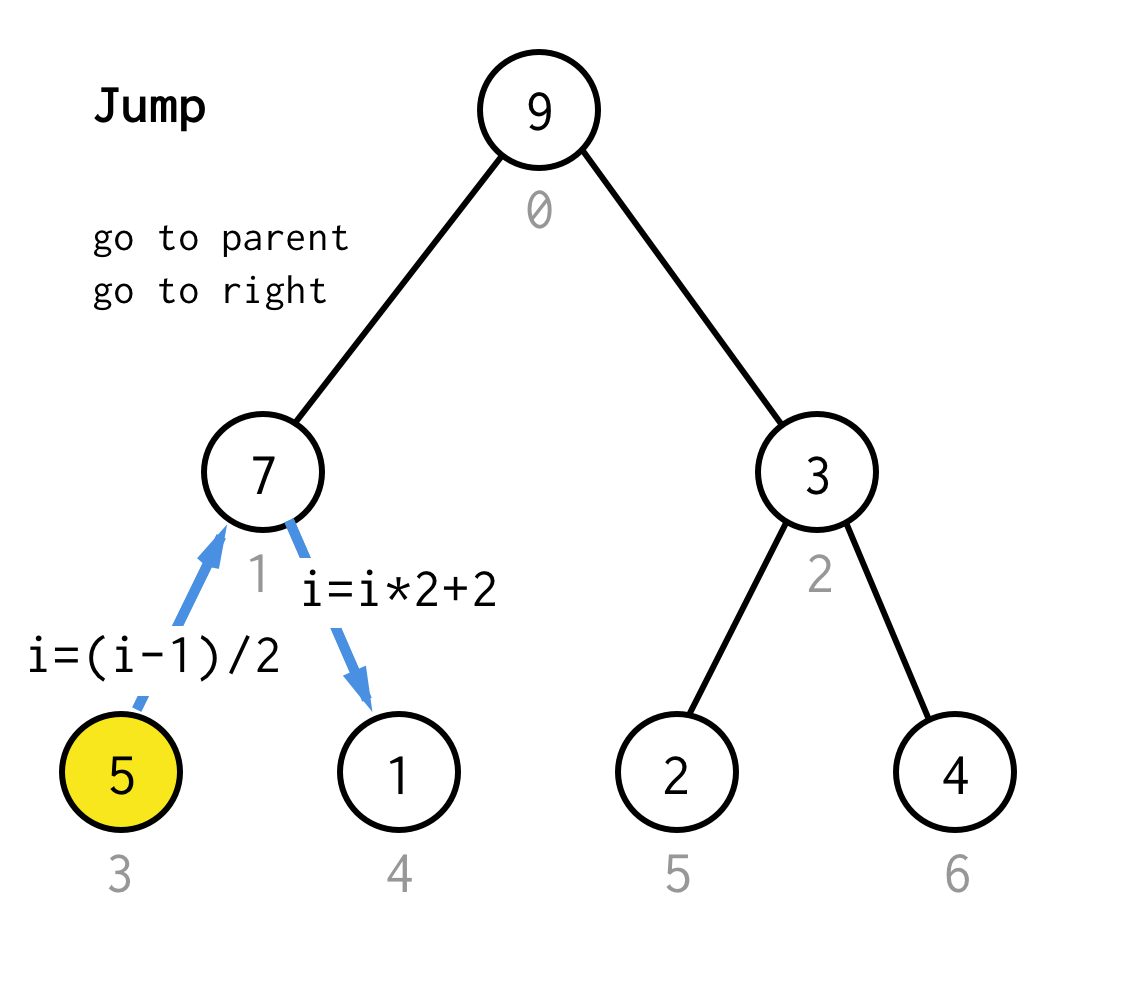
Taka operacja skoku może być zaimplementowana przez zwykłą inkrementację indeksu liścia.Ale kiedy utkniemy w następnym węźle liścia, inkrementacja nie przeniesie węzła do następnego węzła, wymaganego dla DFS.Musimy więc wykonać podwójny skok

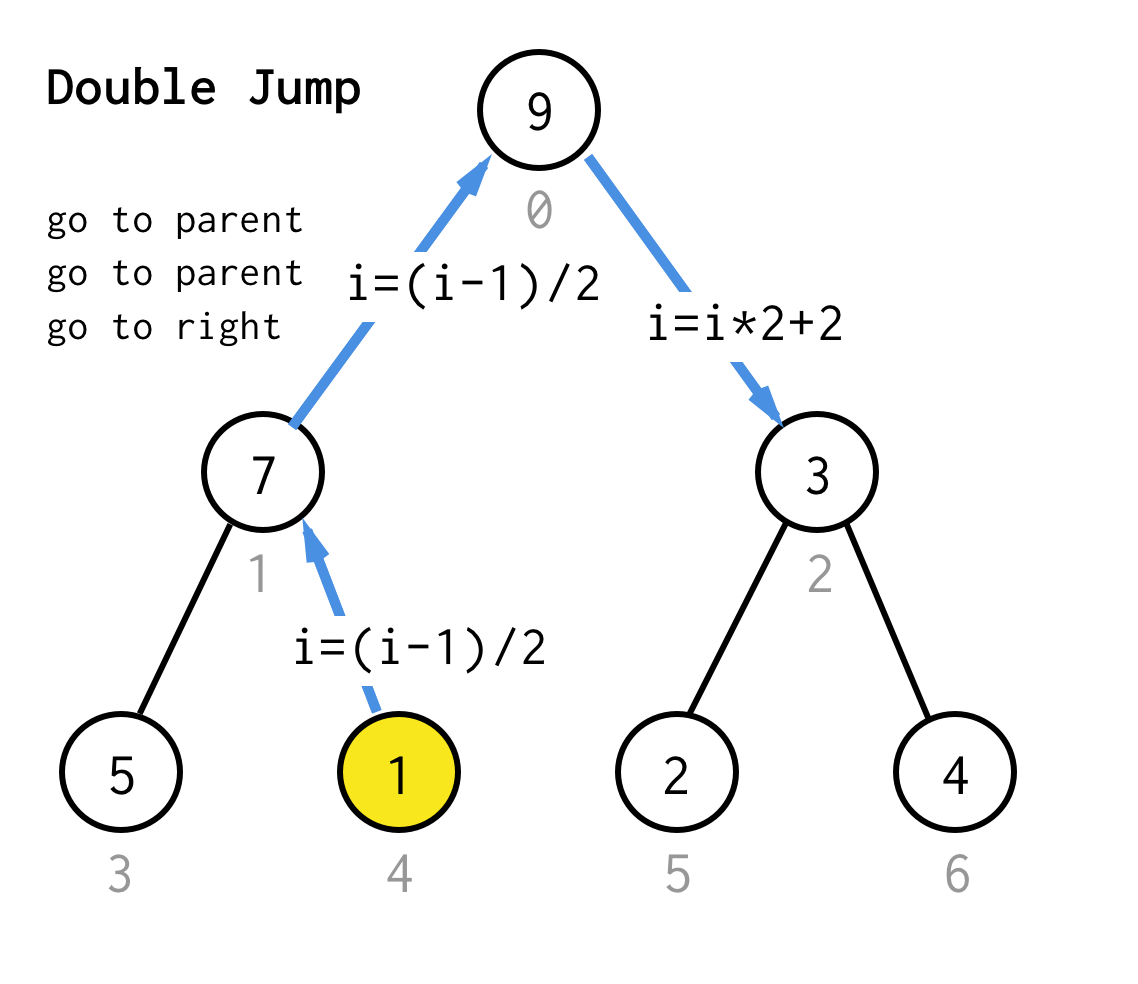
Aby uczynić go bardziej ogólnym, dla naszego algorytmu moglibyśmy zdefiniować operację skok N, która określa ile skoków do rodzica wymaga i zawsze kończy się jednym skokiem do właściwego dziecka.

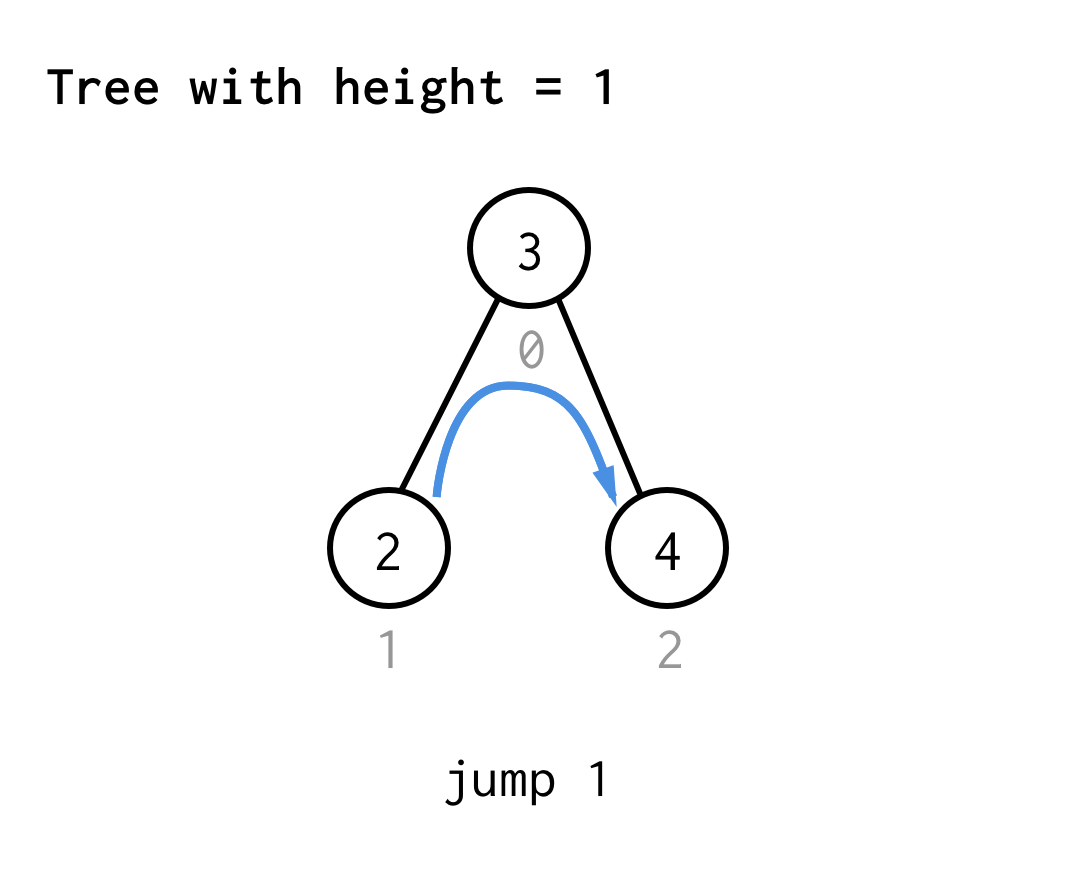
Dla drzewa o wysokości 1, potrzebujemy jednego skoku, skoku 1

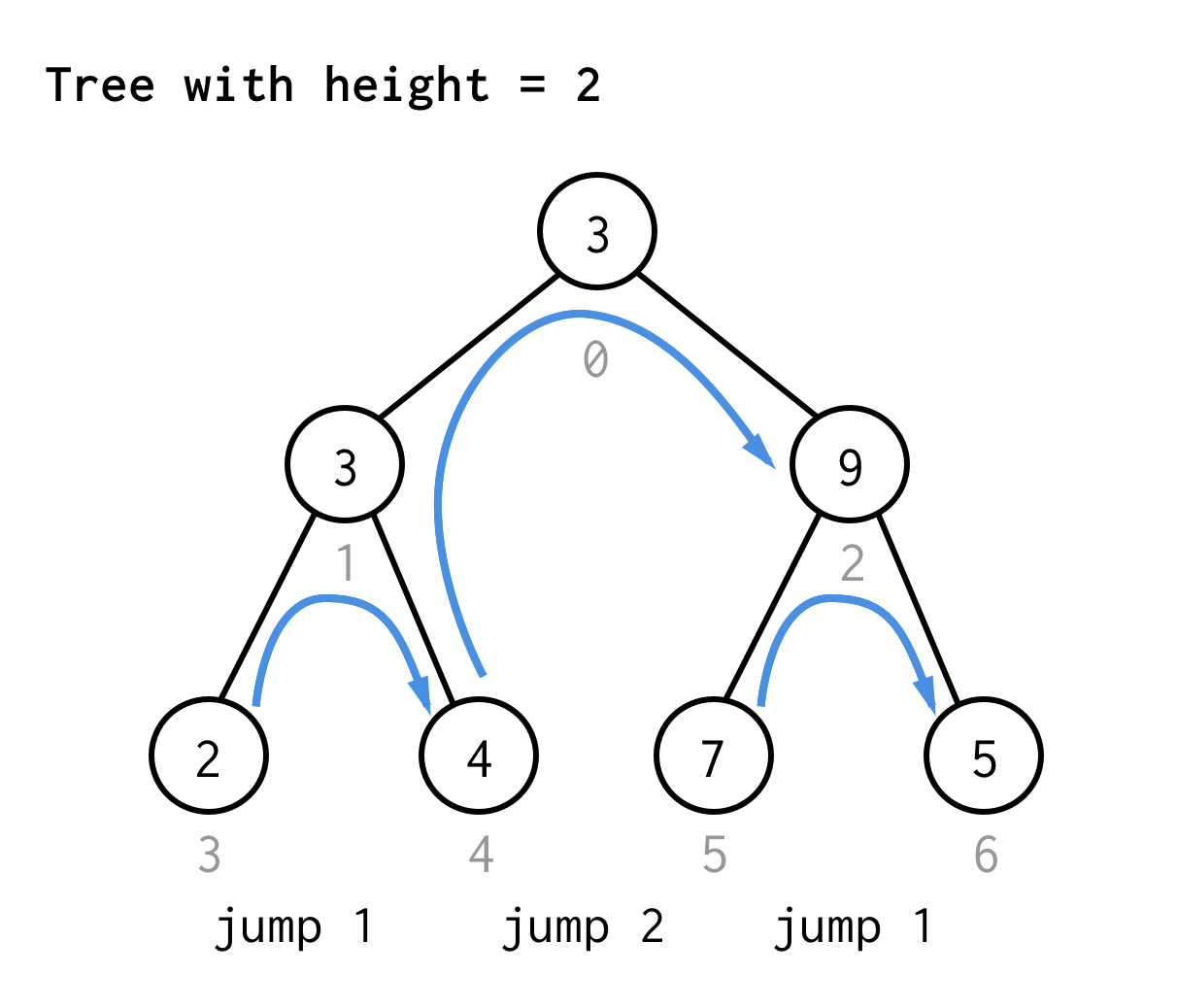
Dla drzewa o wysokości 2, potrzebujemy jednego skoku, jednego podwójnego skoku, a następnie jednego skoku ponownie

Dla drzewa o wysokości 3, można zastosować te same zasady i uzyskać 7 skoków.

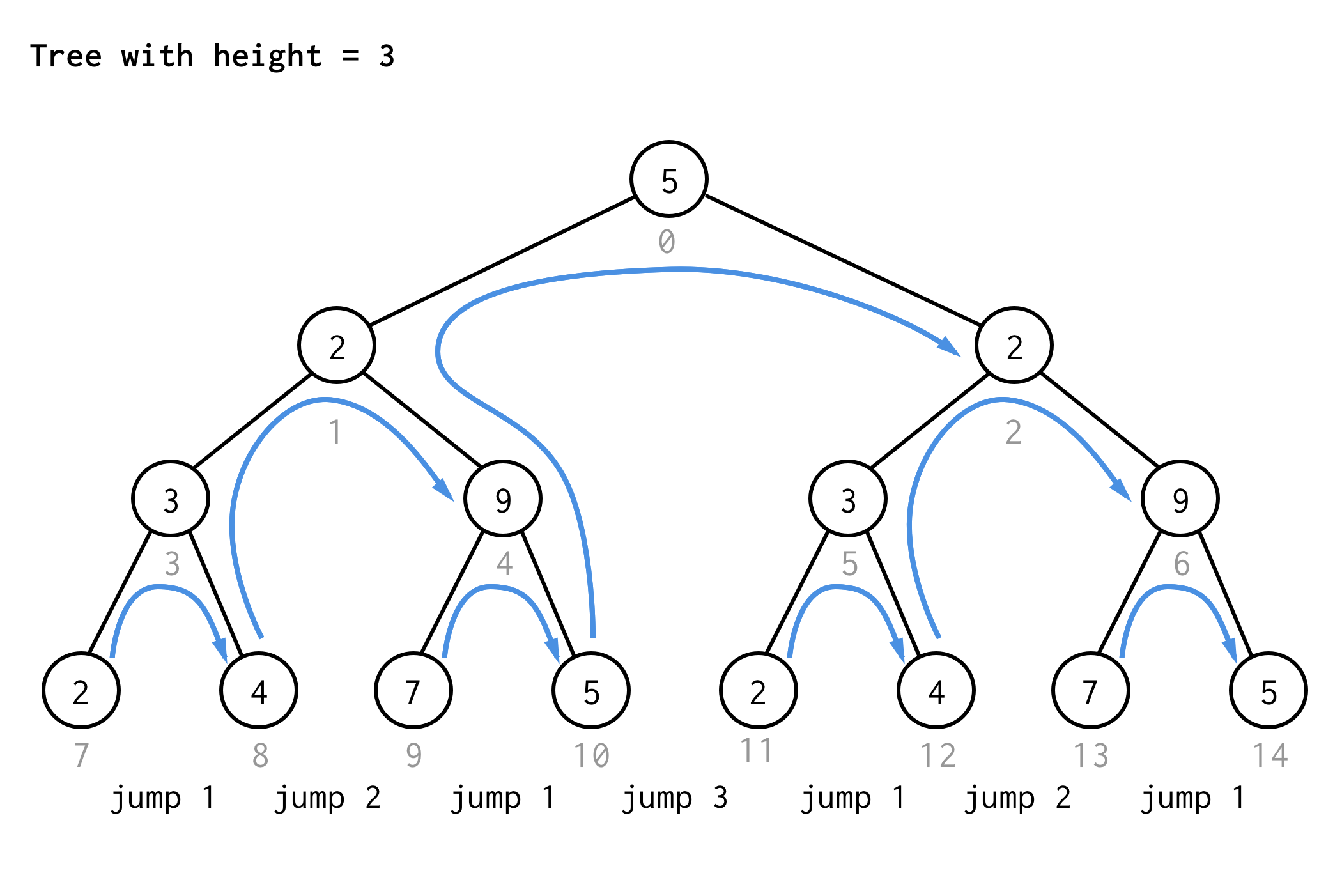
Widzisz wzór?

Jeśli zastosujesz tę samą regułę do drzewa o wysokości 4 i zapiszesz tylko wartości skoków, otrzymasz następny numer sekwencji

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Ta sekwencja znana jest jako słowa Zimina i ma definicję rekurencyjną, co nie jest dobre, ponieważ nie wolno nam używać rekurencji.

Znajdźmy inny sposób, aby to obliczyć.

Jeśli przyjrzysz się uważnie sekwencji skoków, możesz zobaczyć nierekurencyjny wzór.

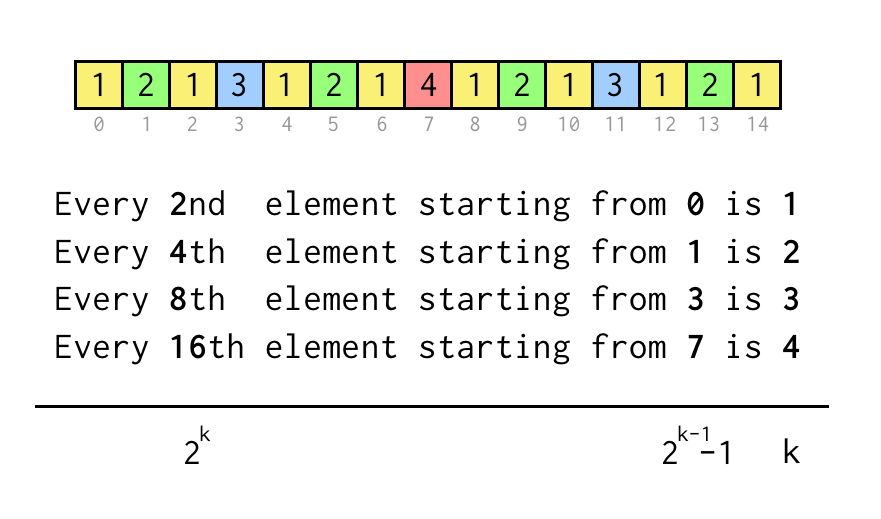
Możemy śledzić indeks dla bieżącego liścia j, który odpowiada indeksowi w tablicy sekwencji powyżej.

Aby zweryfikować stwierdzenie takie jak „Co ósmy element zaczynający się od 3” wystarczy sprawdzić j % 8 == 3, jeśli jest to prawda wymagane są trzy skoki do węzła nadrzędnego.

Iteracyjny proces skoków będzie następujący

• Zacznij od k = 1
• Skocz raz do rodzica stosując i = (i - 1)/2
• Jeśli leaf % 2*k == k - 1 wszystkie skoki wykonane, wyjdź
• W przeciwnym razie ustaw k na 2*k i powtórz.

Jeśli składasz wszystko do kupy, co omówiliśmy

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Done. DFS dla tablicy drzew binarnych bez stosu i rekurencji

Złożoność

Złożoność wygląda jak kwadratowa, ponieważ mamy pętlę w pętli, ale zobaczmy, jaka jest rzeczywistość.

• Dla połowy węzłów całkowitych (n/2) używamy strategii podwajania, która jest stała O(1)
• Dla drugiej połowy węzłów całkowitych (n/2) używamy strategii przeskakiwania liści.
• Połowa węzłów przeskakiwania liści (n/4) wymaga tylko jednego skoku rodzica, 1 iteracji. O(1)
• Połowa z tej połowy (n/8) wymaga dwóch skoków, czyli 2 iteracji. O(1)
• …
• Tylko jeden liść skok węzeł wymaga pełnego skoku do korzenia, który jest O(logN)
• Tak więc, jeśli wszystkie przypadki ma O(1) z wyjątkiem jednego, który jest O(logN), możemy powiedzieć, że średnia dla skoku to O(1)
• Całkowita złożoność to O(n)

Wydajność

Chociaż teoria jest dobra, zobaczmy, jak ten algorytm działa w praktyce, porównując z innymi.

Testujemy 5 algorytmów, używając JMH.

• BFS na drzewie binarnym (lista połączona jako kolejka)
• BFS na tablicy drzew binarnych (wyszukiwanie liniowe)
• DFS na drzewie binarnym (stos)
• DFS na Binary Tree Array (stack)
• Iterative DFS na Binary Tree Array

Wstępnie utworzyliśmy drzewo i używając predykatu do dopasowania ostatniego węzła,aby upewnić się, że zawsze trafiamy w tę samą liczbę węzłów dla wszystkich algorytmów.

Więc, wyniki

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Oczywiście, BFS na tablicy wygrywa. Jest to po prostu wyszukiwanie liniowe, więc jeśli możesz reprezentować drzewo binarne jako tablicę, zrób to.

Iteracyjny DFS, który właśnie opisaliśmy w artykule, zajął 2drugie miejsce i 4.5 razy wolniej niż wyszukiwanie liniowe (BFS na tablicy)

Pozostałe trzy algorytmy są nawet wolniejsze niż iteracyjny DFS, prawdopodobnie dlatego, że wymagają dodatkowych struktur danych, dodatkowej przestrzeni i alokacji pamięci.

A najgorszym przypadkiem jest BFS na drzewie binarnym. Podejrzewam, że tutaj połączona lista jest problemem.

Conclusion

Binary Tree Array jest ładną sztuczką do reprezentowania hierarchicznej struktury danych jako statycznej tablicy (contiguous region w pamięci). Definiuje prostą relację indeksu dla przejścia z rodzica do dziecka, jak również przejście z dziecka do rodzica, co nie jest możliwe z klasyczną binarną reprezentacją tablicy. Niektóre wady, jak powolne wstawianie/usuwanie istnieją, ale jestem pewien, że istnieje wiele zastosowań dla tablicy drzewa binarnego.

Jak pokazaliśmy, algorytmy wyszukiwania, BFS i DFS zaimplementowane na tablicach są znacznie szybsze niż ich bracia na strukturze opartej na referencjach. Dla rzeczywistych problemów nie jest to tak ważne i prawdopodobnie nadal będę używał tablicy binarnej opartej na referencjach.

Anyway, to było miłe ćwiczenie. Spodziewaj się pytania „DFS na tablicy binarnej bez rekursji i stosu” na następnym wywiadzie.

• algorytmy
• datastruktury
• programowanie

mishadoff 10 września 2017 r.