Molekularne momenty dipolowe
W cząsteczkach zawierających więcej niż jedno wiązanie polarne, molekularny moment dipolowy jest po prostu kombinacją wektorową tego, co można uznać za indywidualne „momenty dipolowe wiązań”. Z matematycznego punktu widzenia, momenty dipolowe są wektorami; posiadają zarówno wielkość jak i kierunek. Moment dipolowy cząsteczki jest więc sumą wektorową momentów dipolowych poszczególnych wiązań w cząsteczce. Jeśli momenty dipolowe poszczególnych wiązań znoszą się wzajemnie, to nie ma momentu dipolowego netto. Tak jest w przypadku CO2, cząsteczki liniowej (rysunek rzedu). Każde wiązanie C-O w CO2 jest polarne, a jednak eksperymenty pokazują, że cząsteczka CO2 nie posiada żadnego momentu dipolowego. Ponieważ dwa dipole wiązań C-O w CO2 są równej wielkości i zorientowane względem siebie pod kątem 180°, znoszą się. W rezultacie cząsteczka CO2 nie ma momentu dipolowego netto, mimo że posiada znaczną separację ładunków. W przeciwieństwie do tego, cząsteczka H2O nie jest liniowa (Rysunek \); jest wygięta w przestrzeni trójwymiarowej, więc momenty dipolowe nie znoszą się wzajemnie. Tak więc cząsteczka taka jak H2O ma moment dipolowy netto. Spodziewamy się, że koncentracja ładunku ujemnego będzie na tlenie, atomie bardziej elektronegatywnym, a ładunku dodatniego na dwóch hydrogenach. Ta polaryzacja ładunku pozwala H2O na tworzenie wiązań wodorowych z innymi spolaryzowanymi lub naładowanymi gatunkami, w tym z innymi cząsteczkami wody.
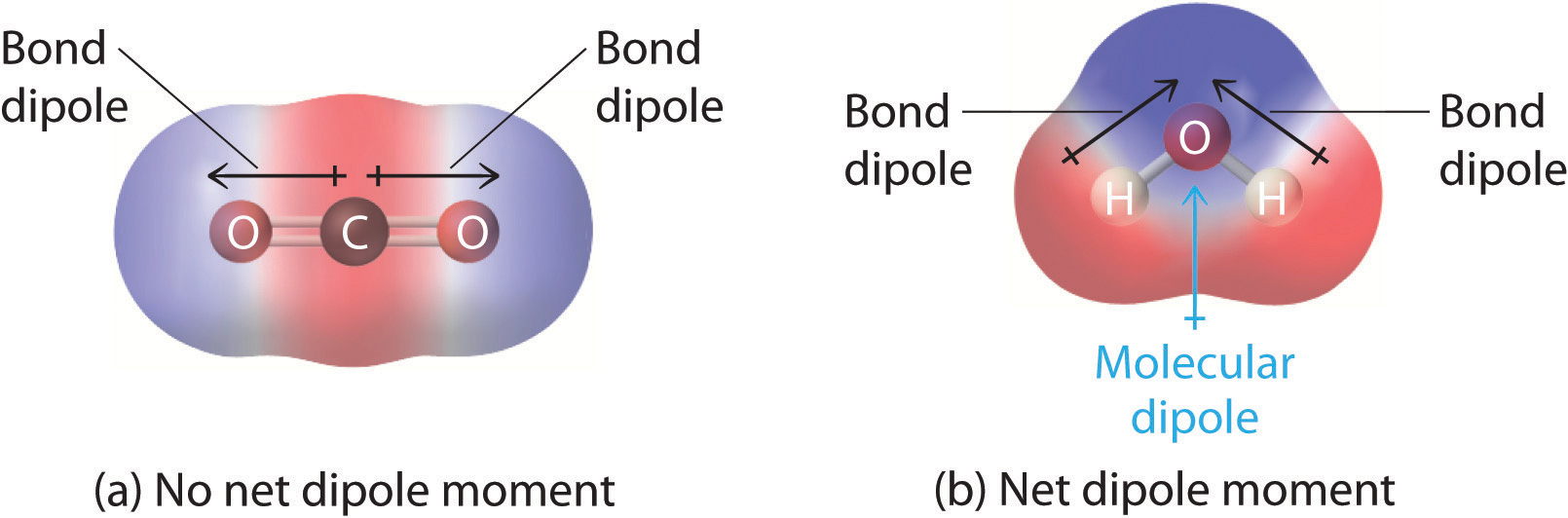
Rysunek: Jak poszczególne momenty dipolowe wiązań są sumowane w celu uzyskania ogólnego molekularnego momentu dipolowego dla dwóch trójatomowych cząsteczek o różnej strukturze. (a) W CO2, dipole wiązania C-O są równe co do wielkości, ale zorientowane w przeciwnych kierunkach (pod kątem 180°). Ich suma wektorowa wynosi zero, więc CO2 nie ma dipoli netto. (b) W H2O dipole wiązania O-H są również równe co do wielkości, ale są zorientowane względem siebie pod kątem 104,5°. Stąd suma wektorowa nie jest równa zero, a H2O ma moment dipolowy netto.
Poniżej przedstawiono uproszczone równanie dla prostego rozdzielonego układu dwuładunkowego, występującego w cząsteczkach dwuatomowych lub przy rozpatrywaniu dipoli wiązań wewnątrz cząsteczki.
Ten dipol wiązania, µ (greckie mu) jest interpretowany jako dipol pochodzący od separacji ładunków na dystansie \(r\) pomiędzy ładunkami cząstkowymi \(Q^+\) i \(Q^-\) (lub bardziej powszechnie używane terminy \(δ^+\) – \(δ^-\)); orientacja dipola jest wzdłuż osi wiązania. Jednostkami momentów dipolowych są zazwyczaj deby (D), gdzie jeden debye jest równy 3,336 x 1030 kulombometrów (C – m) w jednostkach SI. Rozważmy prosty układ pojedynczego elektronu i protonu oddzielonych od siebie stałą odległością. Jednostkowy ładunek elektronu wynosi 1,60 X 1019 C, a proton & elektrony są od siebie oddalone o 100 pm (mniej więcej długość typowego wiązania kowalencyjnego), moment dipolowy oblicza się jako:
&= (1,60 ∗ razy 10^{-19} C)(1,00 ∗ razy 10^{-10} ∗ m) ∗ &= 1,60 ∗ razy 10^{-29} \C ™ ™dot m ™label{2}
&= 4,80; D ∙label{3} \(4.80; D) jest kluczową wartością odniesienia i reprezentuje czysty ładunek +1 i -1 oddzielony o 100 pm. Jeśli jednak separacja ładunków jest większa to moment dipolowy wzrasta (liniowo):
- Gdyby proton i elektron były oddzielone o 120 pm:
- Jeśli proton i elektron byłyby oddzielone o 150 pm:
- Jeśli proton i elektron byłyby oddzielone o 200 pm:
Przykład: Woda
Cząsteczka wody na rysunku \(\) może być użyta do wyznaczenia kierunku i wielkości momentu dipolowego. Z elektronegatywności tlenu i wodoru wynika, że różnica wynosi 1,2e dla każdego z wiązań wodorowo-tlenowych. Następnie, ponieważ tlen jest bardziej elektronegatywnym atomem, wywiera on większe przyciąganie na współdzielone elektrony; posiada on również dwie samotne pary elektronów. Z tego można wywnioskować, że moment dipolowy skierowany jest pomiędzy dwoma atomami wodoru w stronę atomu tlenu. Korzystając z powyższego równania obliczamy, że moment dipolowy wynosi 1,85 D, mnożąc odległość między atomami tlenu i wodoru przez różnicę ładunków między nimi, a następnie znajdując składowe każdego z nich, które wskazują w kierunku momentu dipolowego netto (kąt cząsteczki wynosi 104.5˚).
Moment wiązania wiązania O-H =1,5 D, więc moment dipolowy netto wynosi
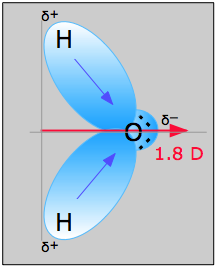
.
Dodaj komentarz