La velocità sincrona è la velocità di rivoluzione del campo magnetico nell’avvolgimento statorico del motore. È la velocità alla quale la forza elettromotrice è prodotta dalla macchina alternata. La velocità sincrona è data dalla relazione mostrata qui sotto.
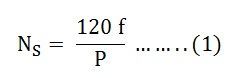
L’equazione precedente (1) mostra che la velocità del rotore N ha una relazione costante con i poli del campo e la frequenza della tensione generata nell’avvolgimento d’indotto. Una macchina che funziona a velocità sincrona è chiamata macchina sincrona. Così, una macchina a corrente alternata in cui il rotore si muove a una velocità e costruisce una relazione costante tra la frequenza della tensione nell’avvolgimento d’indotto e il numero di poli si chiama una macchina sincrona.
La tabella seguente fornisce il numero di poli e le velocità sincrone per una frequenza di potenza di 50 hertz.
| Numero di poli | Velocità sincrona NS in r.p.m |
|---|---|
| 2 | 3000 |
| 4 | 1500 |
| 6 | 1000 |
| 8 | 750 |
| 10 | 600 |
| 12 | 500 |
Relazione tra velocità e frequenza
La frequenza della tensione generata dipende dal numero di poli del campo e dalla velocità di rotazione dei poli del campo. Un ciclo completo di tensione è generato in una bobina dell’indotto quando una coppia di poli di campo passa sopra la bobina.
Lascia che,
- P sia il numero totale di poli di campo,
- p è la coppia dei poli di campo,
- N è la velocità del campo in giri al minuto (r.p.m),
- n è la velocità del campo in giri al secondo (r.p.s), e
- f è la frequenza della tensione generata in hertz.
Come sappiamo,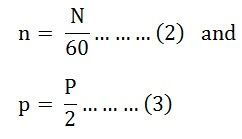
In una rivoluzione del rotore, una bobina dell’indotto è tagliata da P/2 poli nord e P/2 poli sud. Poiché un ciclo è generato in una bobina d’indotto quando una coppia di poli del campo passa sulla bobina. Il numero di cicli generati da una rivoluzione del rotore. Sarà uguale al numero di coppie di poli, cioè,
- Numero di cicli per rivoluzione = p
- Numero di giri al secondo = n
Ora, la frequenza sarà,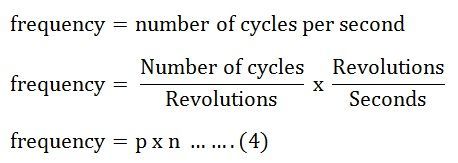
Mettendo il valore di n e p dall’equazione (2) e (3) nell’equazione (4) otterremo
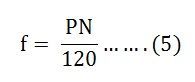
La precedente equazione (3) e (5) dà la relazione tra il numero di poli, velocità e frequenza.
Lascia un commento