X

Privacy & Cookies

Questo sito usa i cookies. Continuando, accetti il loro utilizzo. Per saperne di più, compreso come controllare i cookie.

Ho capito!

Pubblicità

Una spirale è una curva che “emana da un punto, allontanandosi man mano che ruota intorno al punto”.

Ci sono molti tipi diversi di spirali a seconda delle formule che le creano. In questo post del blog, parlerò delle spirali bidimensionali (si noti che esiste anche una varietà di spirali tridimensionali).

Spirale Archimedea

Questa è una spirale che prende il nome dal famoso matematico greco Archimede, che fu il primo a descriverla nel suo libro sulle spirali. È descritta dalla seguente equazione polare:

\, r=a+b\theta

dove a e b sono numeri reali.

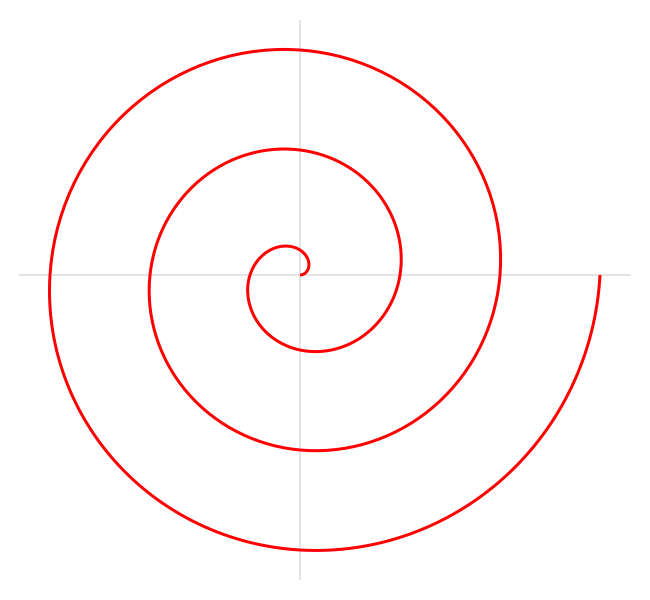
Cambiando il parametro a la spirale gira e il parametro b controlla la distanza tra i giri successivi.

La spirale di Fermat

La spirale di Fermat è una spirale parabolica che obbedisce alla seguente equazione polare:

r=\pm \theta ^{1/2}\,

È un tipo di spirale Archimedea.

Spirale di Eulero

Conosciuta anche come Spirale di Cornu, è una curva la cui curvatura cresce all’aumentare della distanza dall’origine; “la curvatura di una curva circolare è uguale al reciproco del raggio”.

La forma parametrica consiste in due equazioni con gli intervalli di Fresnel, che possono essere risolti solo approssimativamente.

S(x)=\int_0^x \sin(t^2)\,\mathrm{d}t,\quad C(x)=\int_0^x \cos(t^2)\mathrm{d}t.

Questi integrali, e quindi la spirale di Eulero, possono essere usati per descrivere la distribuzione di energia della diffrazione di Fresnel ad una singola fenditura nella teoria delle onde.

Spirale iperbolica

Prima concepita da Pierre Varignon nel 1704, la spirale iperbolica è una curva trascendentale, cioè “è una funzione analitica che non soddisfa una equazione polinomiale”. È l’opposto di una spirale archimedea e quindi ha la seguente equazione polare:

r={\frac {a}{\theta }}

Nel centro, è a distanza infinita dal polo; per θ che parte da 0, r parte all’infinito.

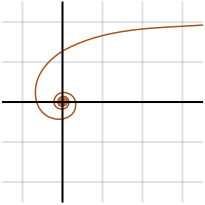
Lituus

Il lituus è una spirale con equazione polare:

r^2\theta = k \2001>

dove k è una costante. Quindi, l’angolo è inversamente proporzionale al quadrato del raggio.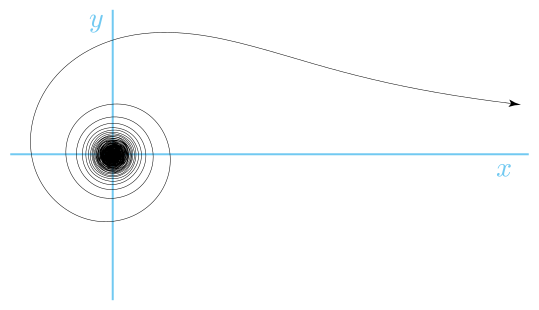

La curva fu chiamata così da Roger Cotes in una raccolta di articoli pubblicati nel 1722, in onore dell’antico lituus romano (un bastone augurale curvo o tromba da guerra).

Spirale logaritmica

La spirale logaritmica è una spirale autosimile, che appare spesso in natura. Fu descritta per la prima volta da Cartesio, ma fu studiata a fondo da Jacob Bernoulli che la chiamò “la spirale meravigliosa”. Ha un’equazione polare di

.