pensieri di Mishadoff

Implementare la ricerca Depth-First per l’Albero Binario senza stack e ricorsione.

Albero Binario Array

Questo è un albero binario.

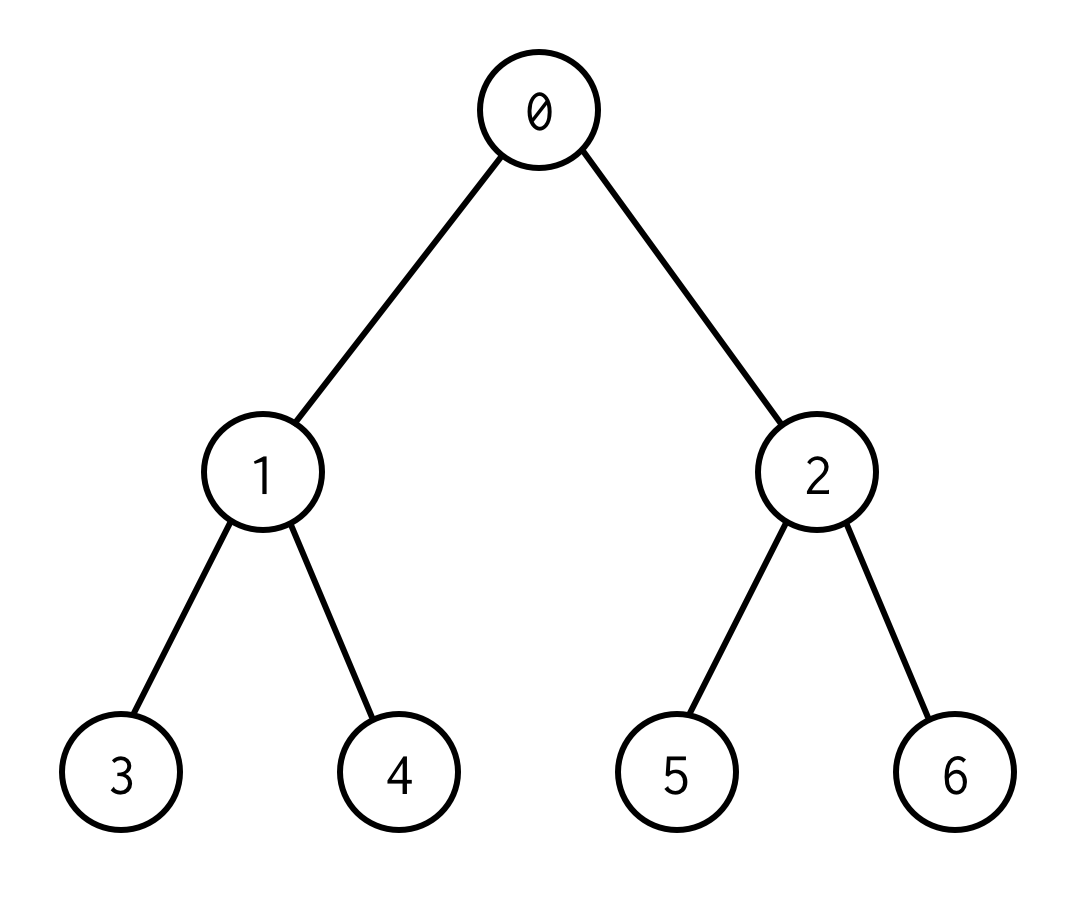
0 è un nodo radice.
0ha due figli: sinistra 1 e destra: 2.
Ognuno dei suoi figli ha i suoi figli e così via.
I nodi senza figli sono nodi foglia (3,4,5,6).

Il numero di bordi tra i nodi radice e i nodi foglia definisce l’altezza dell’albero.L’albero sopra ha l’altezza 2.

L’approccio standard per implementare l’albero binario è definire una classe chiamata BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Tuttavia, c’è un trucco per implementare l’albero binario usando solo array statici.

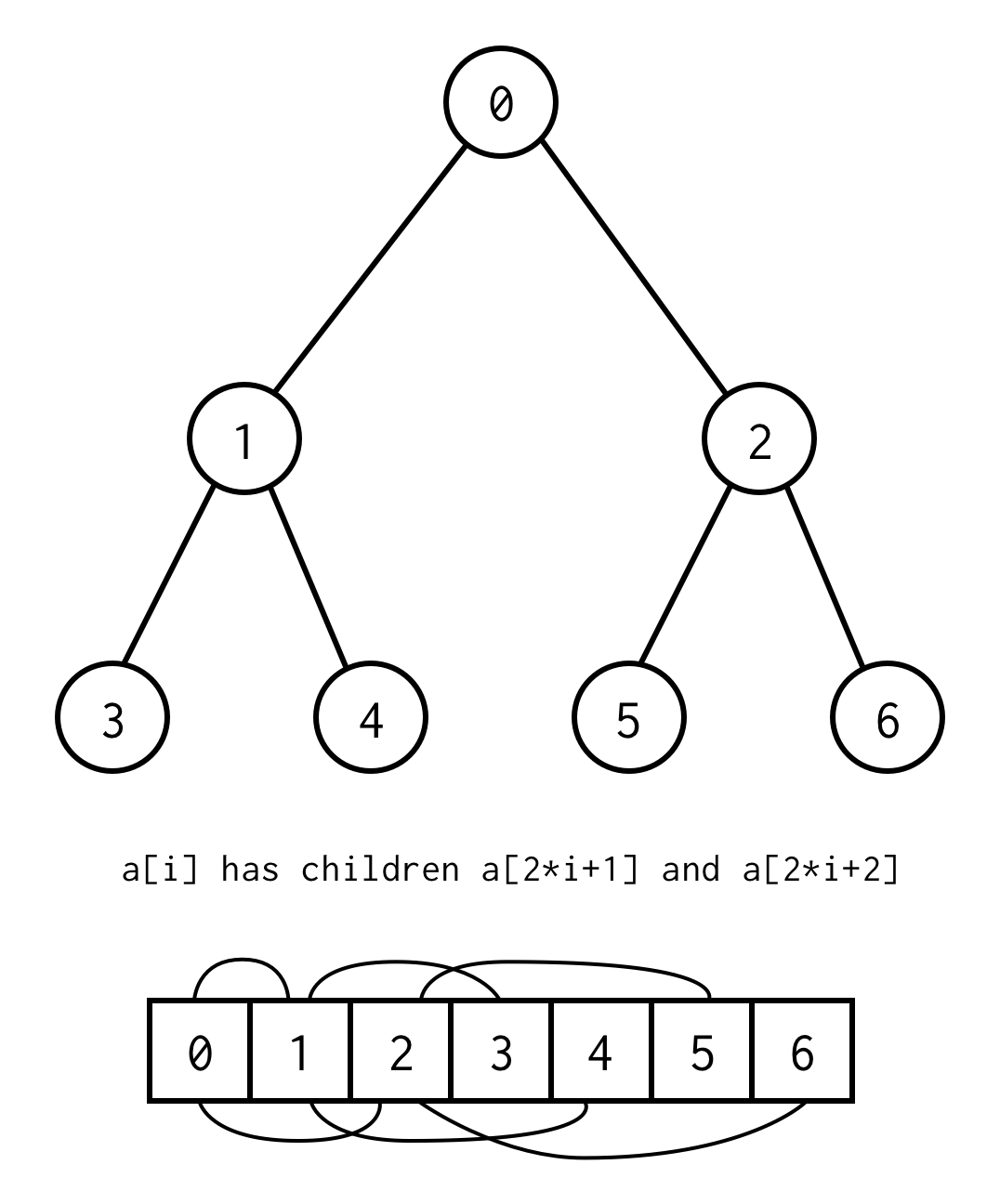
La relazione tra l’indice del genitore e l’indice del figlio, ci permette di spostarci dal genitore al figlio, così come dal figlio al genitore

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Nota importante che l’albero deve essere completo, il che significa che per la specifica altezza deve contenere esattamente elementi.

Puoi evitare tale requisito mettendo null al posto degli elementi mancanti.L’enumerazione si applica anche ai nodi vuoti. Questo dovrebbe coprire ogni possibile albero binario.

Questa rappresentazione di array per l’albero binario la chiameremo Binary Tree Array.

BFS vs DFS

Esistono due algoritmi di ricerca per l’albero binario: breadth-first search (BFS) e depth-first search (DFS).

Il modo migliore per capirli è visivamente

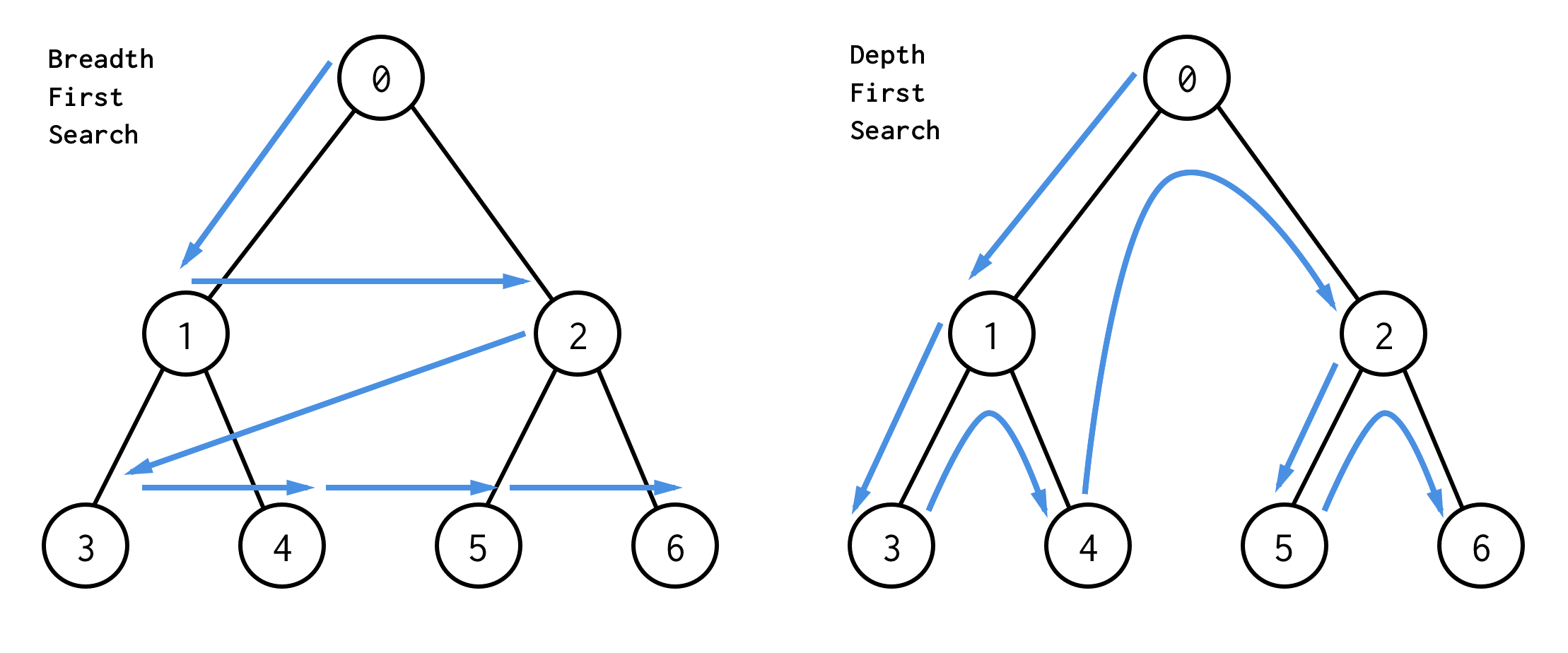
BFS cerca i nodi livello per livello, partendo dal nodo principale. Poi controlla i suoi figli. Poi i figli per i figli e così via, fino a quando tutti i nodi vengono elaborati o viene trovato il nodo che soddisfa la condizione di ricerca.

DFS si comporta diversamente. Controlla tutti i nodi dal percorso più a sinistra dalla radice alla foglia, poi salta su e controlla il nodo di destra e così via.

Per gli alberi binari classici BFS implementato usando la struttura dati Queue (LinkedList implementa Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Se si sostituisce queue con lo stack si ottiene l’implementazione DFS.

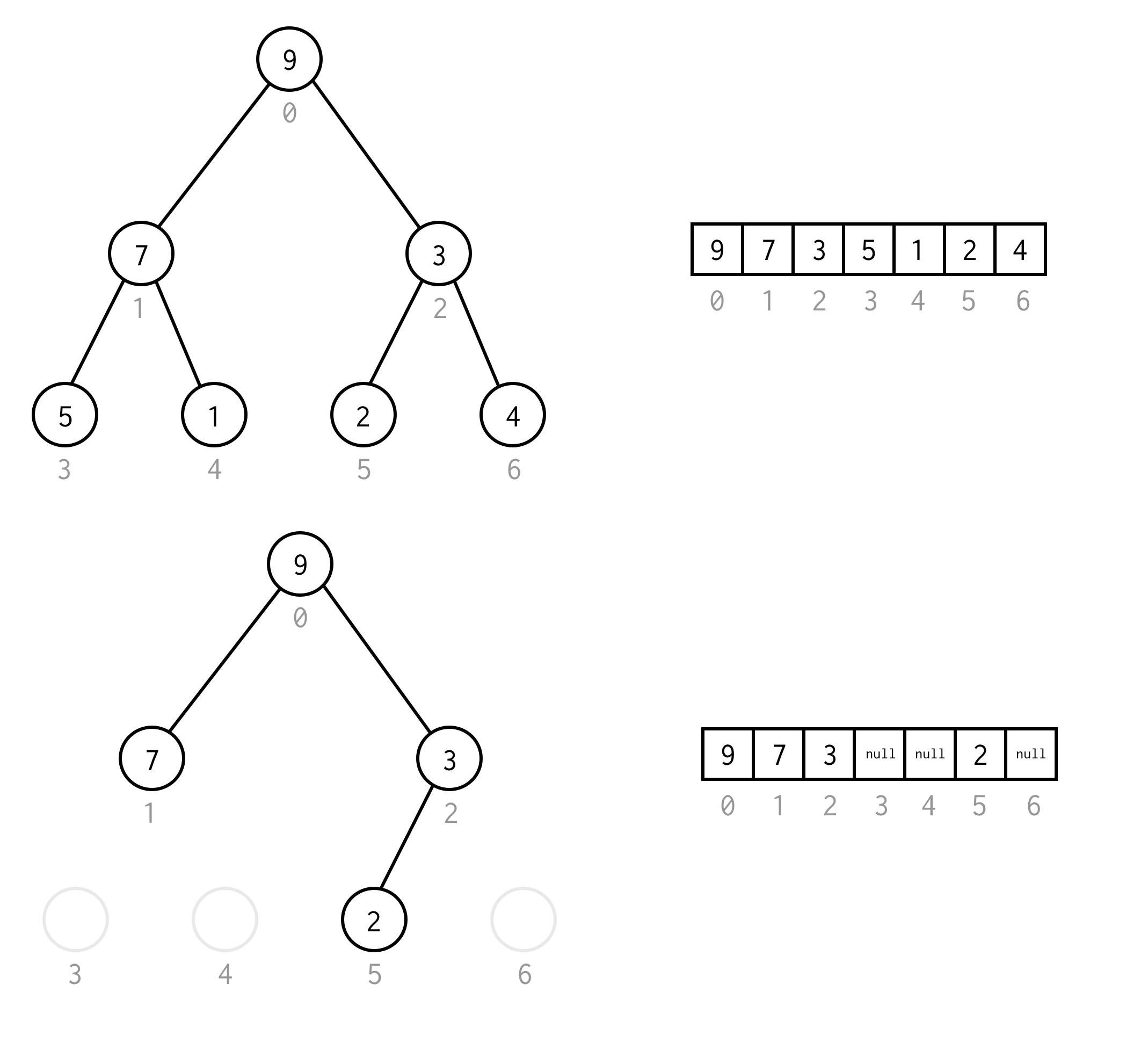
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Per esempio, supponiamo che abbiate bisogno di trovare il nodo con valore 1 nel seguente albero.

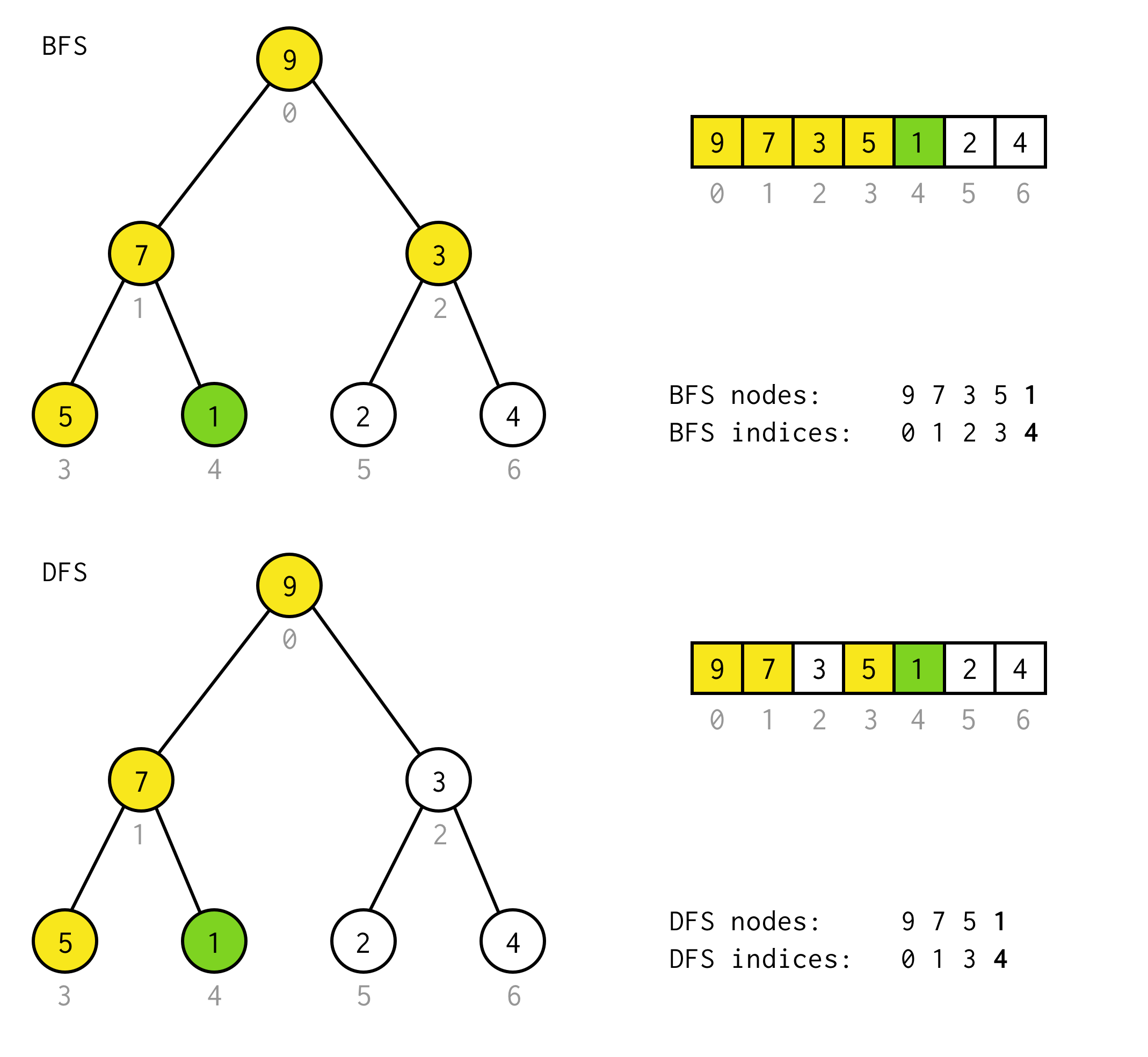
Le celle gialle sono celle che vengono testate nell’algoritmo di ricerca prima di trovare il nodo necessario.Tenete conto che per alcuni casi DFS richiede meno nodi per l’elaborazione.Per alcuni casi ne richiede di più.

BFS e DFS per l’array di alberi binari

La ricercareadth-first per l’array di alberi binari è banale.Poiché gli elementi nell’array di alberi binari sono posizionati livello per livello e bfs controlla anche gli elementi livello per livello, bfs per l’array di alberi binari è solo ricerca lineare

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

La ricerca depth-first è un po’ più difficile.

Utilizzando la struttura dati dello stack potrebbe essere implementato allo stesso modo del classico albero binario, basta mettere gli indici nello stack.

Da questo punto la ricorsione non è affatto diversa, si usa solo lo stack implicito delle chiamate al metodo invece dello stack della struttura dati.

E se potessimo implementare DFS senza stack e ricorsione.Alla fine è solo una selezione dell’indice corretto ad ogni passo?

Bene, proviamo.

DFS per Binary Tree Array (senza stack e ricorsione)

Come in BFS iniziamo dall’indice radice 0.
Poi abbiamo bisogno di ispezionare il suo figlio sinistro, il cui indice potrebbe essere calcolato dalla formula 2*i+1.
Chiamiamo il processo di andare al prossimo figlio sinistro raddoppiando.

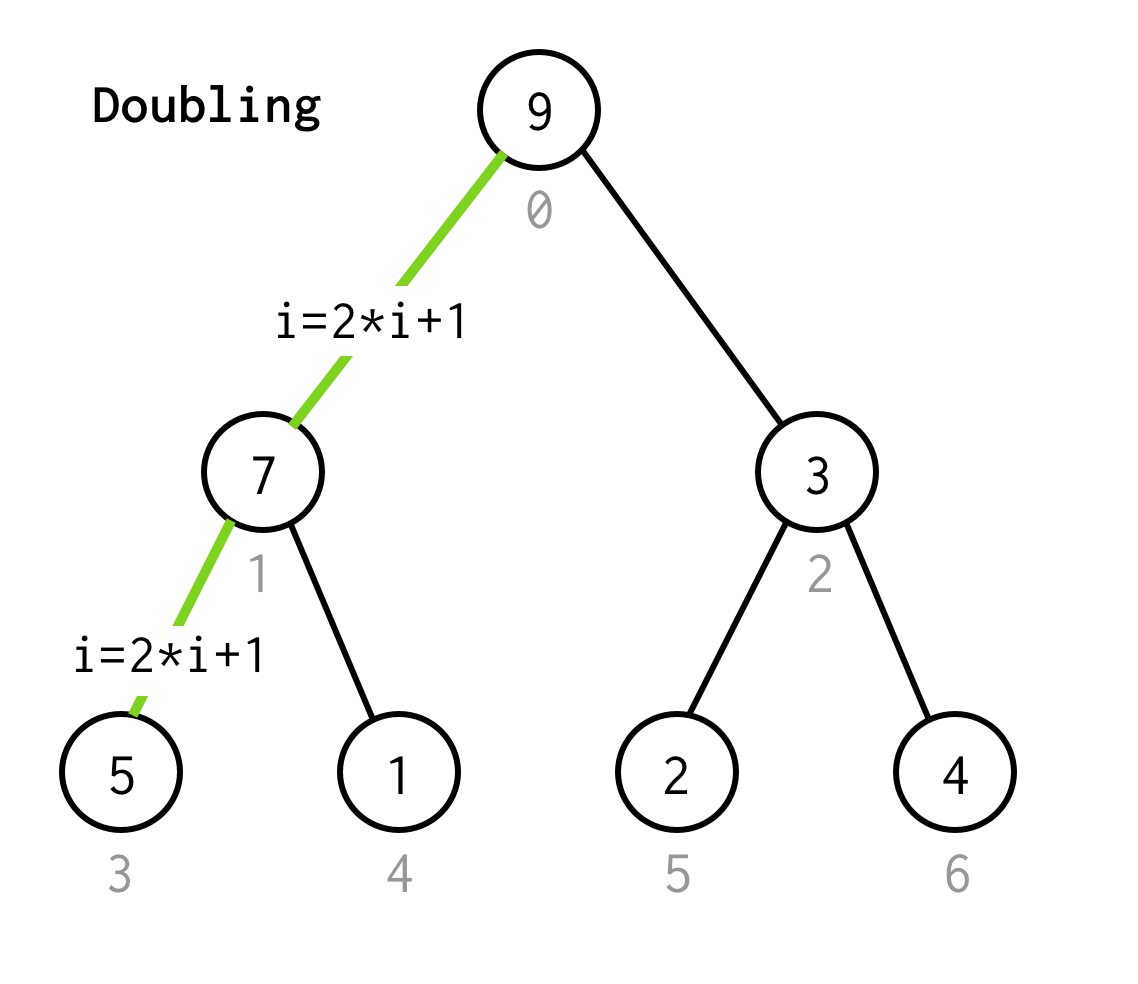
Continuiamo a raddoppiare l’indice finché non ci fermiamo al nodo foglia.

Quindi come possiamo capire che è un nodo foglia?

Se il prossimo figlio di sinistra produce un’eccezione di indice fuori dai limiti dell’array, dobbiamo smettere di raddoppiare e saltare al figlio di destra.

Questa è una soluzione valida, ma possiamo evitare di raddoppiare inutilmente.L’osservazione qui è che il numero di elementi nell’albero di alcuni height è due volte più grande (e più uno) dell’albero con height - 1.

Per l’albero con height = 2 abbiamo 7 elementi, per l’albero con height = 3 abbiamo 7*2+1 = 15 elementi.

Utilizzando questa osservazione costruiamo la semplice condizione

i < array.length / 2

Si può controllare che questa condizione sia valida per qualsiasi nodo non foglia nell’albero.

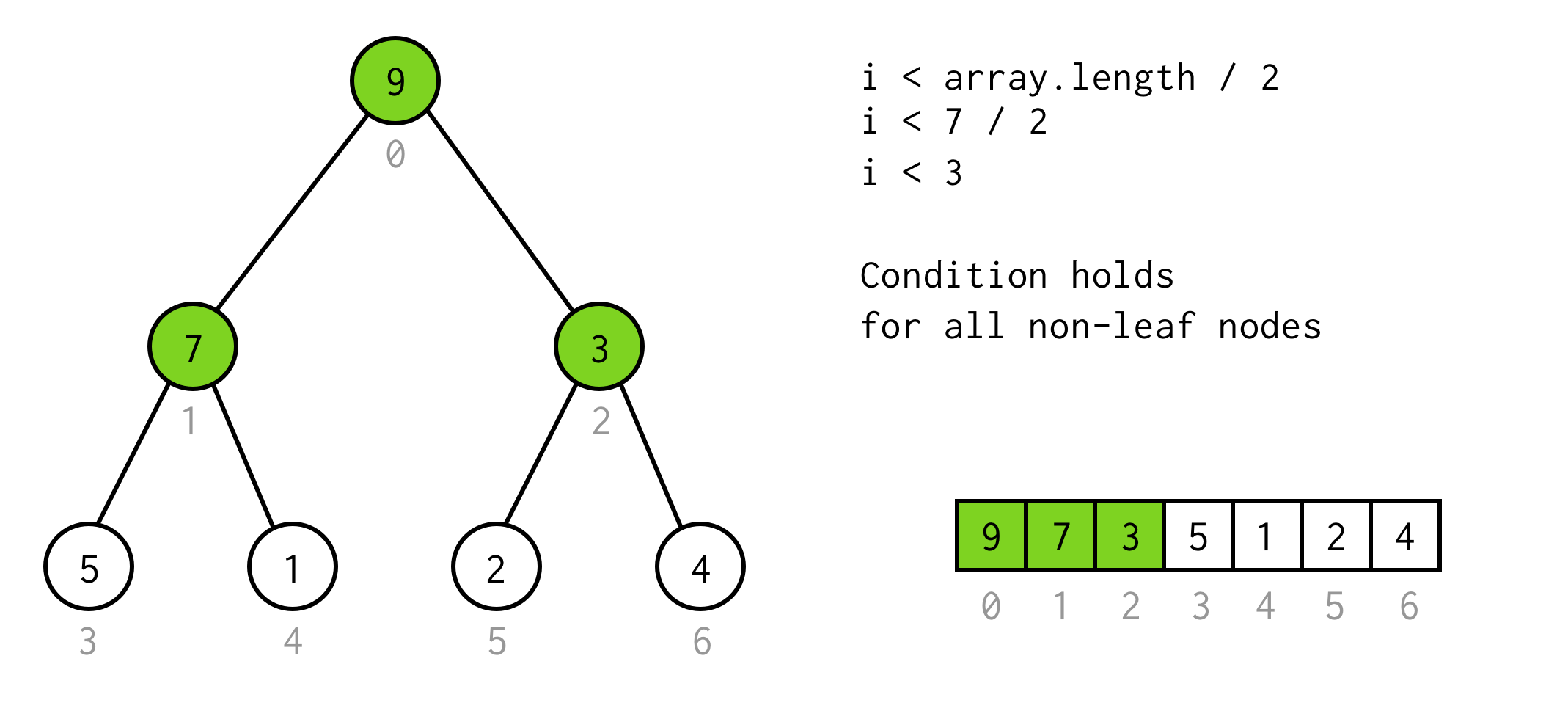
Bene, finora. Possiamo eseguire il raddoppio, e sappiamo anche quando fermarci, ma in questo modo possiamo controllare solo i figli sinistri dei nodi.

Quando siamo bloccati al nodo foglia e non possiamo più applicare il raddoppio, eseguiamo l’operazione di salto.Fondamentalmente, se il raddoppio è andare al figlio sinistro, il salto è andare al genitore e andare al figlio destro.

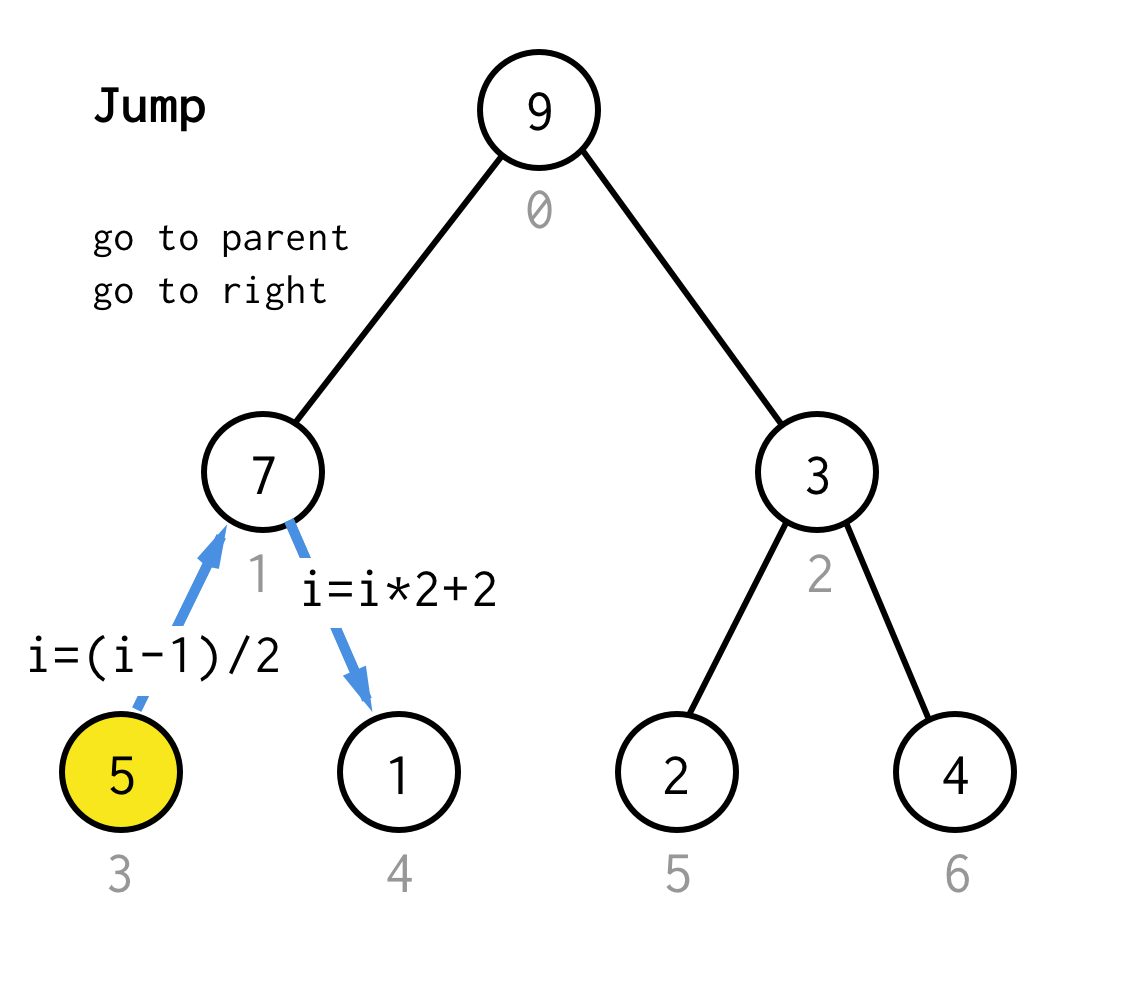
Questa operazione di salto può essere implementata semplicemente incrementando l’indice della foglia.Ma quando siamo bloccati al prossimo nodo foglia, l’incremento non sposta il nodo al nodo successivo, richiesto per DFS.Quindi abbiamo bisogno di fare un doppio salto

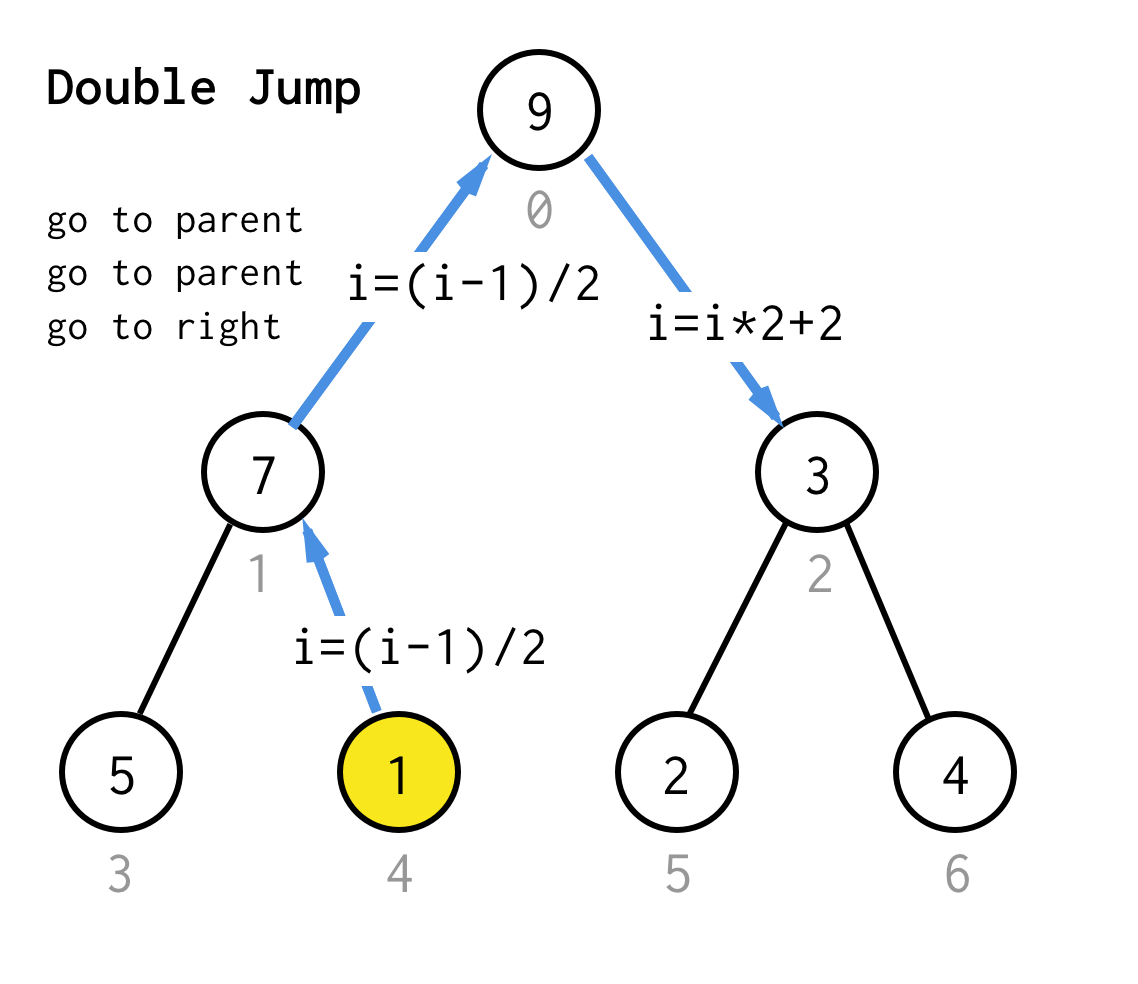
Per renderlo più generico, per il nostro algoritmo potremmo definire l’operazione salto N, che specifica quanti salti al genitore richiede e finisce sempre con un salto al figlio giusto.

Per l’albero con altezza 1, abbiamo bisogno di un salto, il salto 1

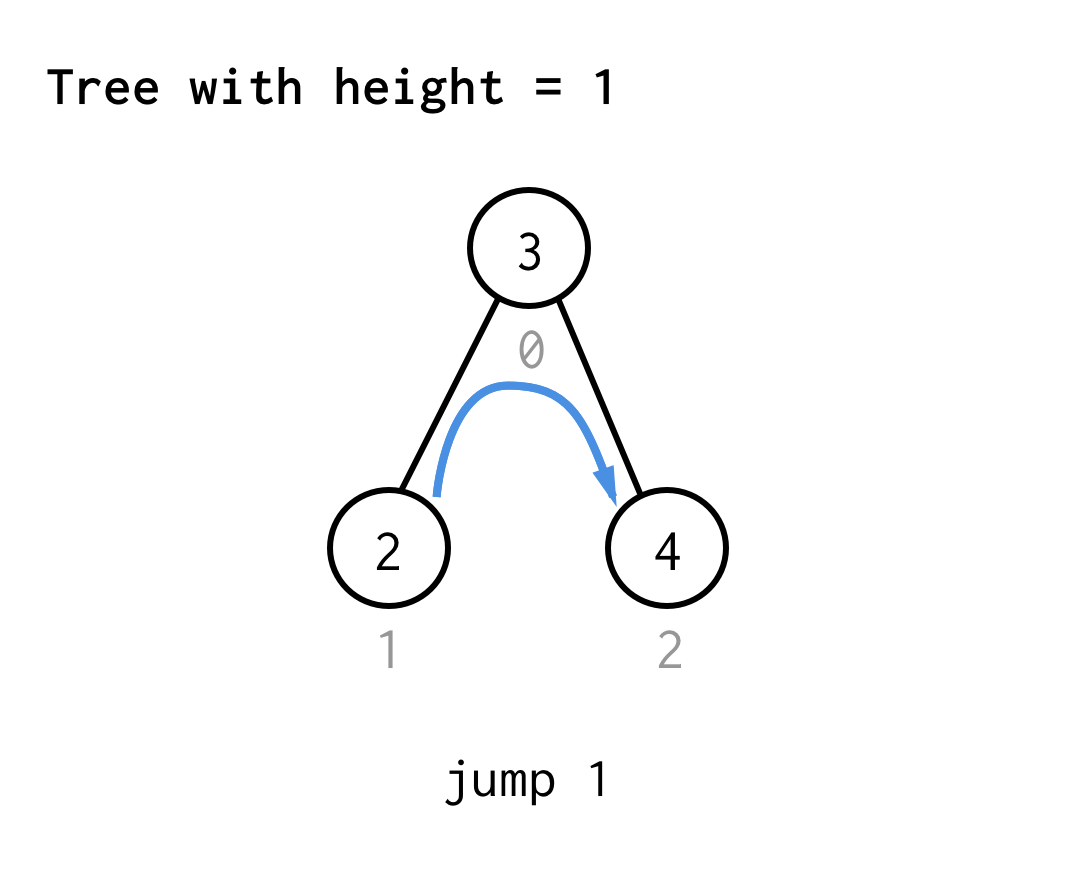
Per l’albero con altezza 2, abbiamo bisogno di un salto, un doppio salto, e poi ancora un salto

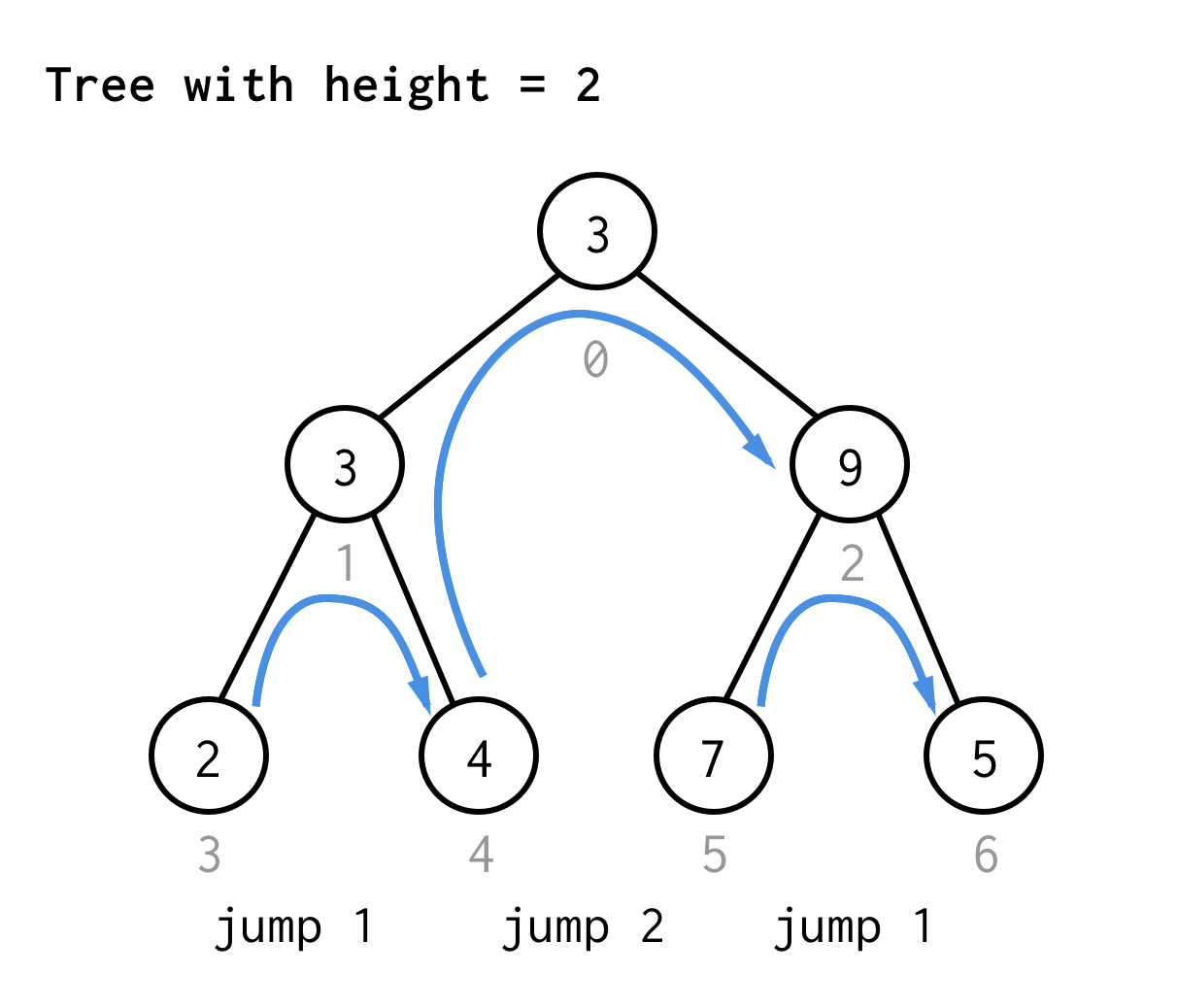
Per l’albero con altezza 3, potete applicare le stesse regole e ottenere 7 salti.

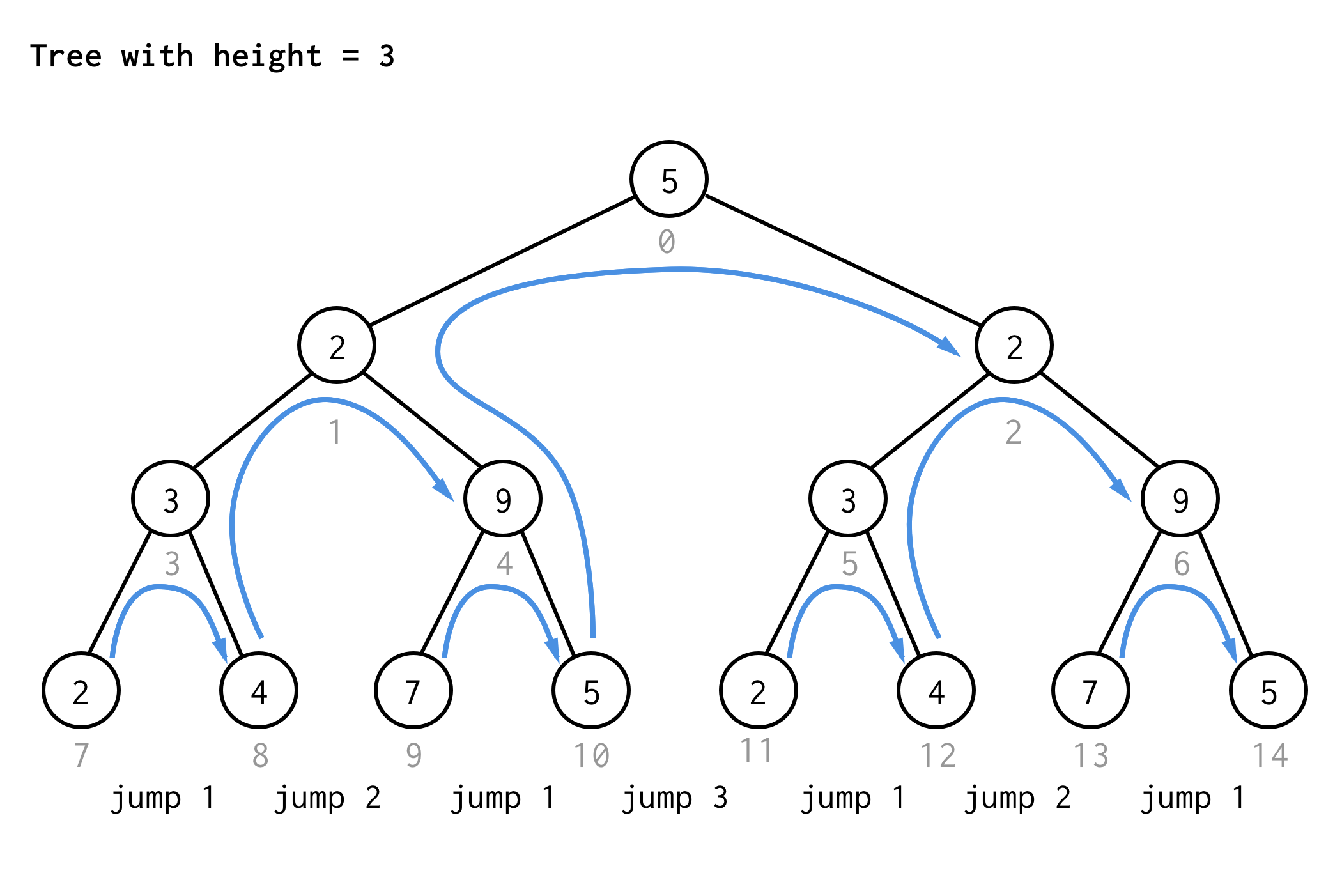
Vedi lo schema?

Se applichi la stessa regola all’albero di altezza 4 e scrivi solo i valori dei salti otterrai il prossimo numero di sequenza

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Questa sequenza conosciuta come parole di Zimin e ha una definizione ricorsiva, che non è grande, perché non ci è permesso usare la ricorsione.

Cerchiamo un altro modo per calcolarla.

Se si guarda attentamente la sequenza di salto, si può vedere un modello non ricorsivo.

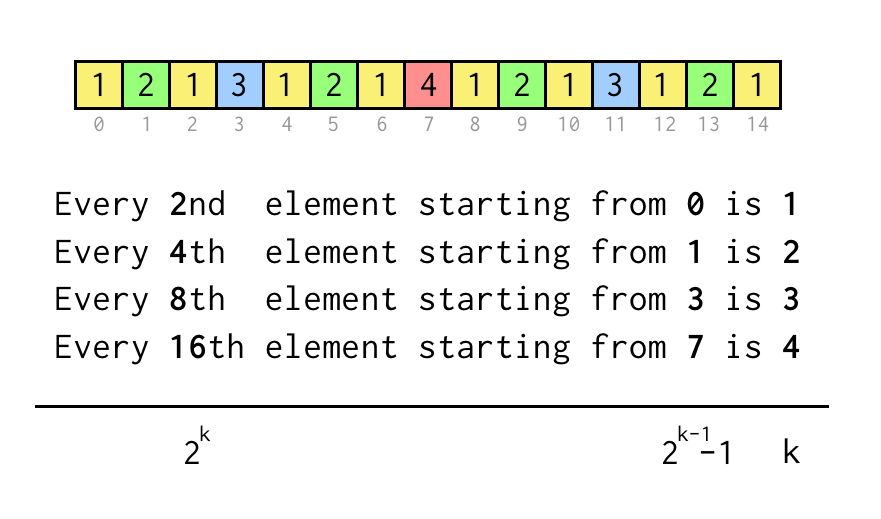
Possiamo rintracciare l’indice per la foglia corrente j, che corrisponde all’indice nell’array della sequenza sopra.

Per verificare un’affermazione come “Ogni 8° elemento a partire da 3” controlliamo solo j % 8 == 3, se è vero tre salti al nodo padre richiesto.

Il processo iterativo di salto sarà il seguente

• Inizia con k = 1
• Salta una volta al genitore applicando i = (i - 1)/2
• Se leaf % 2*k == k - 1 tutti i salti eseguiti, esci
• Altrimenti, imposta k a 2*k e ripeti.

Se si mette tutto insieme quello che abbiamo discusso

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Fatto. DFS per array di alberi binari senza stack e ricorsione

Complessità

La complessità sembra quadratica perché abbiamo loop in un loop, ma vediamo qual è la realtà.

• Per la metà dei nodi totali (n/2) usiamo la strategia del raddoppio, che è costante O(1)
• Per l’altra metà dei nodi totali (n/2) usiamo la strategia del salto delle foglie.
• La metà dei nodi del salto delle foglie (n/4) richiede solo un salto del genitore, 1 iterazione. O(1)
• La metà di questa metà (n/8) richiede due salti, o 2 iterazioni. O(1)
• …
• Solo un nodo fogliare che salta richiede un salto completo alla radice, che è O(logN)
• Quindi, se tutti i casi hanno O(1) tranne uno che è O(logN), possiamo dire che la media per il salto è O(1)
• La complessità totale è O(n)

Performance

Anche se la teoria è buona, vediamo come funziona questo algoritmo in pratica, confrontandolo con altri.

Testiamo 5 algoritmi, usando JMH.

• BFS su albero binario (lista collegata come coda)
• BFS su matrice di alberi binari (ricerca lineare)
• DFS su albero binario (stack)
• DFS on Binary Tree Array (stack)
• DFS iterativo su Binary Tree Array

Abbiamo precreato un albero e usato un predicato per abbinare l’ultimo nodo,per essere sicuri di colpire sempre lo stesso numero di nodi per tutti gli algoritmi.

Così, risultati

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Ovviamente, BFS su array vince. È solo una ricerca lineare, quindi se puoi rappresentare l’albero binario come array, fallo.

Il DFS iterativo, che abbiamo appena descritto nell’articolo, ha preso 2il secondo posto e 4.5le volte più lento della ricerca lineare (BFS su array)

I restanti tre algoritmi sono ancora più lenti del DFS iterativo, probabilmente, perché coinvolgono strutture dati aggiuntive, spazio extra e allocazione di memoria.

E il caso peggiore è BFS su albero binario. Sospetto che qui la lista collegata sia un problema.

Conclusione

Binary Tree Array è un bel trucco per rappresentare una struttura dati gerarchica come un array statico (regione contigua nella memoria). Definisce una semplice relazione di indice per spostarsi da genitore a figlio, così come per spostarsi da figlio a genitore, cosa che non è possibile con la rappresentazione classica di array binario. Esistono alcuni svantaggi, come l’inserimento/cancellazione lenta, ma sono sicuro che ci sono molte applicazioni per gli array ad albero binario.

Come abbiamo dimostrato, gli algoritmi di ricerca, BFS e DFS implementati sugli array sono molto più veloci dei loro fratelli su una struttura basata sui riferimenti. Per i problemi del mondo reale non è così importante, e, probabilmente, userò ancora l’array binario basato sul riferimento.

Ad ogni modo, è stato un bell’esercizio. Aspettati la domanda “DFS su array binario senza ricorsione e stack” nella tua prossima intervista.

• algoritmi
• datastructures
• programmazione

mishadoff 10 settembre 2017