Autovettore

Gli autovettori sono un insieme speciale di vettori associati a un sistema lineare di equazioni (es.e., un’equazione matriciale) che a volte sono anche conosciuti come vettori caratteristici, vettori propri o vettori latenti (Marcus e Minc 1988, p. 144).

La determinazione degli autovettori e degli autovalori di un sistema è estremamente importante in fisica e in ingegneria, dove è equivalente alla diagonalizzazione della matrice e si presenta in applicazioni comuni come l’analisi della stabilità, la fisica dei corpi rotanti e le piccole oscillazioni dei sistemi vibranti, per nominarne solo alcune. Ogni autovettore è accoppiato con un corrispondente cosiddetto autovalore. Matematicamente, è necessario distinguere due diversi tipi di autovettori: autovettori di sinistra e autovettori di destra. Tuttavia, per molti problemi di fisica e ingegneria, è sufficiente considerare solo gli autovettori di destra. Il termine “autovettore” usato senza qualificazione in tali applicazioni può quindi essere inteso come riferito a un autovettore destro.

La decomposizione di una matrice quadrata in autovalori e autovettori è nota in questo lavoro come decomposizione degli autovettori, e il fatto che questa decomposizione sia sempre possibile finché la matrice composta dagli autovettori di è quadrata è nota come teorema della decomposizione degli autovettori.

Definire un autovettore destro come un vettore colonna che soddisfa

(1)

dove è una matrice, quindi

(2)

il che significa che gli autovalori di destra devono avere determinante zero, cioèe.,

(3)

Similmente, definire un autovettore sinistro come un vettore riga che soddisfa

(4)

Prendendo la trasposizione di ogni lato dà

(5)

che può essere riscritto come

(6)

Riorganizzare nuovamente per ottenere

(7)

che significa

(8)

Riscrivendo dà

			(9)
			(10)
			(11)

dove l’ultimo passo segue dall’identità

(12)

Equando le equazioni (◇) e (11), che sono entrambe uguali a 0 per e arbitrari, richiedono quindi che , cioè, gli autovalori di sinistra e di destra sono equivalenti, un’affermazione che non è vera per gli autovettori.

Lasciamo che sia una matrice formata dalle colonne degli autovettori di destra e sia una matrice formata dalle righe degli autovettori di sinistra. Sia

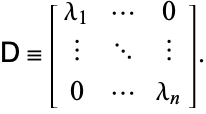(13)

allora

			(14)
			(15)

e

			(16)
			(17)

così

(18)

Ma questa equazione è della forma

(19)

dove è una matrice diagonale, quindi deve essere vero che è anche diagonale. In particolare, se è una matrice simmetrica, allora gli autovettori sinistro e destro sono semplicemente la trasposizione l’uno dell’altro, e se è una matrice autoaddizionale (cioè, è ermitiana), allora gli autovettori sinistro e destro sono matrici contigue.

Gli autovettori possono non essere uguali al vettore zero. Un multiplo scalare non nullo di un autovettore è equivalente all’autovettore originale. Quindi, senza perdita di generalità, gli autovettori sono spesso normalizzati all’unità di lunghezza.

Mentre una matrice ha sempre autovalori, alcuni o tutti degenerati, tale matrice può avere tra 0 e autovettori linearmente indipendenti. Per esempio, la matrice ha solo il singolo autovettore .

Gli autovettori possono essere calcolati nel Wolfram Language utilizzando Eigenvectors. Questo comando restituisce sempre una lista di lunghezza , quindi ogni autovettore che non è linearmente indipendente viene restituito come vettore zero. Gli autovettori e gli autovalori possono essere restituiti insieme usando il comando Eigensystem.

Data una matrice con autovettori , , e e autovalori corrispondenti , , e , allora un vettore arbitrario può essere scritto

(20)

Applicando la matrice ,

			(21)
			(22)

così

(23)

Se , e , segue quindi che

(24)

quindi l’applicazione ripetuta della matrice a un vettore arbitrario sorprendentemente risulta in un vettore proporzionale all’autovettore con autovalore maggiore.