Százalékos hiba képlet

Százalékos hiba számítási képlet

A százalékos hiba képletet a becsült szám és a tényleges szám közötti különbségként számítják ki a tényleges számhoz képest, és százalékban fejezik ki, más szóval egyszerűen a valós szám és a feltételezett szám közötti különbség százalékos formában.

Tudományos vonatkozású kérdésekben gyakran használják a százalékos hiba képlet fogalmát, amelyben a kísérleti érték és a pontos érték közötti eltérést kell meghatározni. Ez a számítás segít abban, hogy a kísérletből származó értéket összehasonlítsuk a pontos vagy valós értékkel. A százalékos hiba arról is tájékoztatást nyújt, hogy a mérés vagy a becslés mennyire áll közel a valódi vagy valós értékhez.

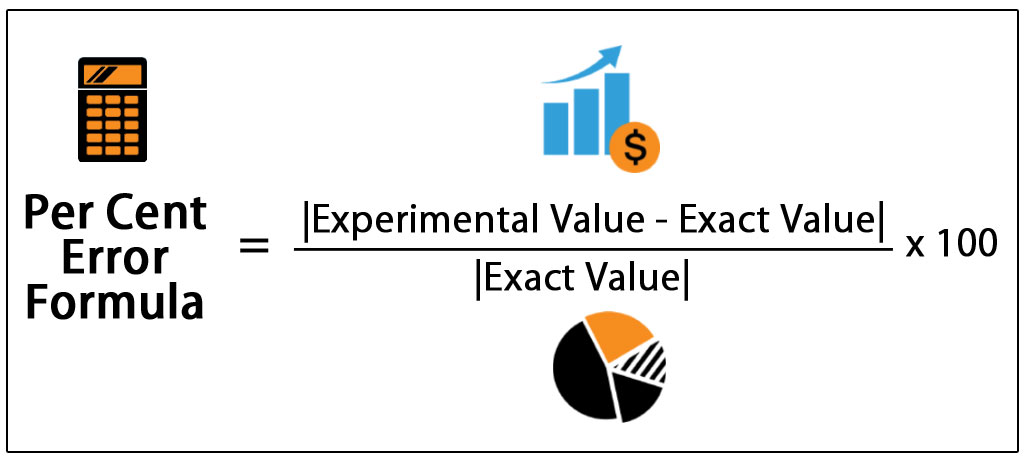
Lépések a százalékos hiba kiszámításához

A százalékos hiba kiszámításához az alábbi lépéseket követhetjük:

• 1. lépés: Először meg kell kapnunk a kísérleti (feltételezett) értéket és a pontos értéket.
• 2. lépés: Meg kell találni a köztük lévő eltérést, majd az abszolút értéket kell venni; vagyis figyelmen kívül kell hagyni minden negatív előjelet, ha van ilyen. Ezt nevezzük hibának.
• 3. lépés: Ezután derítsük ki a pontos vagy valós érték abszolút értékét.
• 4. lépés: Osszuk el a 2. lépésben meghatározott abszolút hibát (nem negatív) az abszolút valós értékkel vagy a pontos értékkel.
• 5. lépés: Most végül szorozzuk meg a 4. lépésben kapott eredményt 100-zal, hogy az eredményt százalékos értékké alakítsuk, majd adjunk az eredményhez egy “%” jelet.

Példák

Példa #1

Az indiai Gudzsarátban nemrég egy új turisztikai hely, az egység szobrát állították fel, és becslések szerint az avatás napján 3.00.000 ember fog megfordulni. De a pontos létszám, amely eljött az avatásra, körülbelül 2,88,000 ember volt. Ki kell számolnia a százalékos hibát.
Az alábbiakban a százalékos hiba kiszámításához megadott adatok

A százalékos hiba kiszámítása tehát a következő lesz,

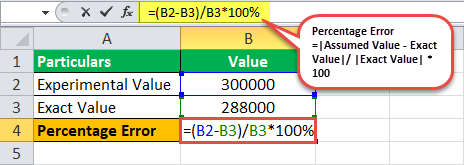
=(300000-288000)/288000*100

százalékos hiba lesz –

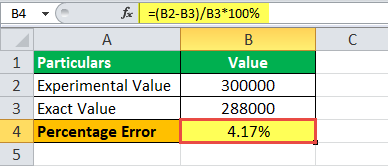
Százalékos hiba= 4,17%

Példa #2

Avenue Supermarket, egy kiskereskedelmi vállalat, amely “Dmart” néven működik, terjeszkedési szakaszban van, és a vállalat új városokban tervezi új fiókok nyitását. A pénzügyi év elején a vállalat 24 üzlet megnyitását tervezte és becsülte, azonban az év végére a vállalat csak 21 üzletet nyitott meg. A vállalat megkereste Önt, hogy számolja ki a kezdeti tervezés során elkövetett százalékos hibát.

Az alábbiakban a százalékos hiba kiszámításához megadott adatok

Ezért a százalékos hiba kiszámítása a következő lesz,

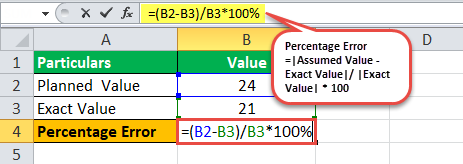
=(24-21)/21*100

A százalékos hiba –

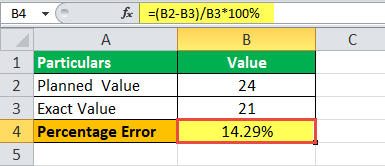
Százalékos hiba= 14,29%

Példa #3

Az egyik hírcsatorna által a választási kampány során végzett felmérés szerint az XYZ párt a 350 helyből 278 mandátumot fog nyerni. Az eredmények kiderülése után kiderült, hogy az XYZ pártnak a 350 helyből 299 helyet sikerült megszereznie. A hírcsatorna értetlenül áll a tényleges eredmény előtt, és most azt szeretné megtudni, hogy milyen margóhibát követtek el, és mennyivel maradtak le. Számítsa ki a százalékos hibát.

Az alábbiakban a százalékos hiba kiszámításához megadott adatok szerepelnek.

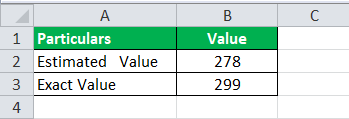
A százalékos hiba kiszámítása tehát a következő lesz,

A százalékos hiba –

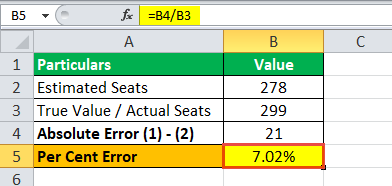
Százalékos hiba=-7,02%

Ez volt az útmutató a százalékos hiba képletéhez. Itt megtanuljuk, hogyan kell kiszámítani a százalékos hibát a képlete segítségével, gyakorlati példákkal és egy letölthető excel-sablonnal. A finanszírozásról többet megtudhat a következő cikkekből –

• Hibahatár
• Szorzótényező képlet
• Százalékos változás Excelben
• képletből of Confidence Interval
• APR vs APY