Adatvédelem & Sütik
Ez az oldal sütiket használ. A folytatással Ön hozzájárul ezek használatához. Tudjon meg többet, beleértve a sütik ellenőrzését.
A spirál olyan görbe, amely “egy pontból indul ki, és a pont körül keringve egyre távolabb kerül”.

A spiráloknak sokféle típusa létezik az őket létrehozó képletektől függően. Ebben a blogbejegyzésben a kétdimenziós spirálokat fogom tárgyalni (megjegyzem, hogy léteznek különféle háromdimenziós spirálok is).
Archimédészi spirál
Ez a spirál a híres görög matematikusról, Arkhimédészről kapta a nevét, aki elsőként írta le a Spirálokról című könyvében. A következő poláris egyenlet írja le:
ahol a és b valós számok.
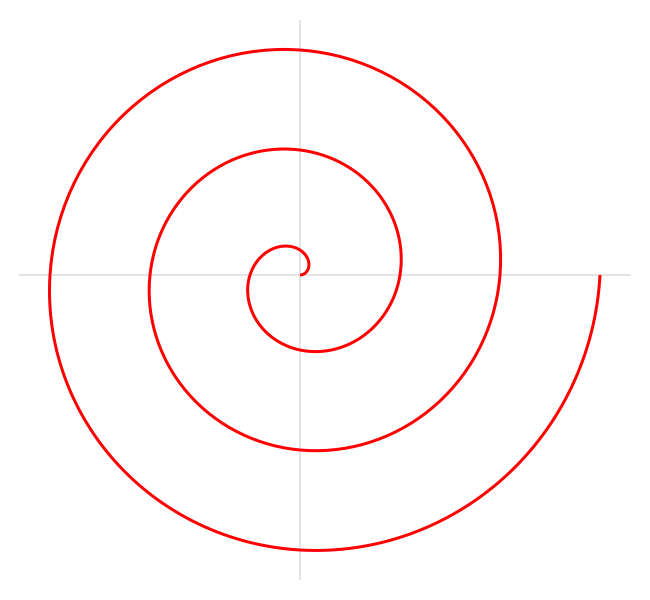
Az a paraméter változtatásával a spirál elfordul, a b paraméter pedig az egymást követő fordulatok közötti távolságot szabályozza.
Fermat spirálja
A Fermat spirál egy parabolikus spirál, amely a következő poláris egyenletnek engedelmeskedik:
Az archimédeszi spirál egyik típusa.

Euler-spirál
Más néven Cornu-spirál, olyan görbe, amelynek görbülete az origótól való távolság növekedésével nő; “a körgörbe görbülete egyenlő a sugár reciprokával”.

A paraméterforma két Fresnel-intervallumú egyenletből áll, amelyek csak közelítőleg oldhatók meg.
Ezek az integrálok, és így az Euler-spirál is használható a hullámelméletben a Fresnel-féle diffrakció energiaeloszlásának leírására egyetlen résen.
Hyperbolikus spirál
A hiperbolikus spirál, amelyet először Pierre Varignon fogalmazott meg 1704-ben, transzcendens görbe, vagyis “olyan analitikus függvény, amely nem elégíti ki a polinomegyenletet”. Ez az archimédeszi spirál ellentéte, és így a következő poláris egyenlete van:
A középpontban a pólustól végtelen távolságra van; 0-ról induló θ esetén r a végtelenben kezdődik.
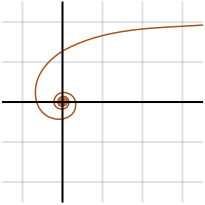
Lituus
A lituus egy spirál, amelynek poláris egyenlete:
ahol k egy állandó. A szög tehát fordítottan arányos a sugár négyzetével. 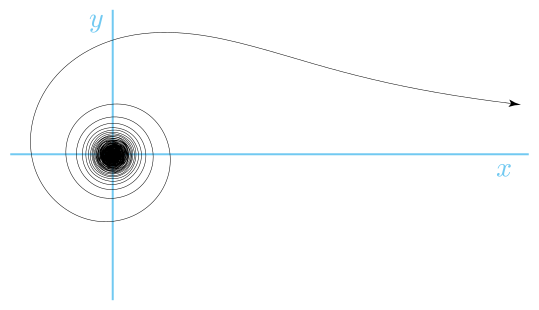
A görbét Roger Cotes egy 1722-ben megjelent tanulmánygyűjteményében az ókori római lituus (ívelt augurális bot vagy haditrombita) után nevezte el.
Logaritmikus spirál
 A logaritmikus spirál egy önhasonló spirál, amely gyakran előfordul a természetben. Először Descartes írta le, de alaposan tanulmányozta Jacob Bernoulli, aki “csodálatos spirálnak” nevezte. Poláris egyenletei a következők:
A logaritmikus spirál egy önhasonló spirál, amely gyakran előfordul a természetben. Először Descartes írta le, de alaposan tanulmányozta Jacob Bernoulli, aki “csodálatos spirálnak” nevezte. Poláris egyenletei a következők:





Vélemény, hozzászólás?