Sajátvektor

Az eigenvektorok egy lineáris egyenletrendszerhez tartozó vektorok egy speciális halmaza (i.e., egy mátrixegyenlethez), amelyeket néha karakterisztikus vektoroknak, sajátvektoroknak vagy látens vektoroknak is neveznek (Marcus és Minc 1988, 144. o.).

Egy rendszer sajátvektorainak és sajátértékeinek meghatározása rendkívül fontos a fizikában és a mérnöki tudományokban, ahol ez egyenértékű a mátrixdiagonalizálással, és olyan gyakori alkalmazásokban merül fel, mint a stabilitáselemzés, a forgó testek fizikája és a rezgő rendszerek kis rezgései, hogy csak néhányat említsünk. Minden egyes sajátvektorhoz egy megfelelő, úgynevezett sajátérték párosul. Matematikailag kétféle sajátvektort kell megkülönböztetni: a bal oldali sajátvektorokat és a jobb oldali sajátvektorokat. A fizika és a mérnöki tudományok számos problémájához azonban elegendő csak a jobb sajátvektorokat figyelembe venni. Az ilyen alkalmazásokban minősítés nélkül használt “sajátvektor” kifejezés ezért a jobb sajátvektorra értendő.

A négyzetes A mátrix sajátértékekre és sajátvektorokra való felbontását ebben a munkában saját dekompozíciónak nevezzük, és azt a tényt, hogy ez a felbontás mindig lehetséges, amíg a sajátvektoraiból álló mátrix négyzetes, saját dekompozíció-tételként ismerjük.

Definiáljuk a jobb sajátvektort olyan oszlopvektornak, amely kielégíti

(1)

ahol egy mátrix, tehát

(2)

amely azt jelenti, hogy a jobb oldali sajátértékeknek nulla determinánssal kell rendelkezniük, i.e.,

(3)

Hasonlóképpen definiáljuk a bal oldali sajátvektort olyan sorvektornak , amely kielégíti

(4)

Az egyes oldalak transzponálása adja

(5)

ami átírható

(6)

Újra átrendezve megkapjuk

(7)

ami azt jelenti

(8)

Újraírva ad

			(9)
			(10)
			(11)

ahol az utolsó lépés az azonosságból

(12)

A (◇) és (11) egyenletek egyenlővé tételéhez, amelyek tetszőleges és esetén egyaránt 0-val egyenlőek, tehát szükséges, hogy , azaz, a bal és jobb sajátértékek ekvivalensek, ami a sajátvektorokra nem igaz.

Legyen a jobb sajátvektorok oszlopaiból képzett mátrix és a bal sajátvektorok soraiból képzett mátrix. Legyen

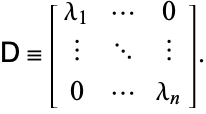(13)

akkor

.

			(14)
			(15)

és

			(16)
			(17)

so

(18)

De ez az egyenlet

formájú.

(19)

ahol egy diagonális mátrix, tehát igaznak kell lennie, hogy szintén diagonális. Különösen, ha szimmetrikus mátrix, akkor a bal és jobb sajátvektorok egyszerűen egymás transzponáltjai, és ha önadjungált mátrix (azaz hermitikus), akkor a bal és jobb sajátvektorok adjungált mátrixok.

A sajátvektorok nem lehetnek egyenlők a nullvektorral. Egy sajátvektor nem nulla skaláris többszöröse egyenértékű az eredeti sajátvektorral. Ezért az általánosság elvesztése nélkül a sajátvektorokat gyakran egységnyi hosszúságra normalizálják.

Míg egy mátrixnak mindig sajátértéke van, amelyek közül néhány vagy mindegyik lehet degenerált, egy ilyen mátrixnak 0 és között lehet lineárisan független sajátvektora. Például a mátrixnak csak egyetlen sajátvektora van.

A Wolfram Nyelvben a sajátvektorok segítségével számíthatók ki a sajátvektorok. Ez a parancs mindig egy hosszúságú listát ad vissza, így minden olyan sajátvektort, amely nem lineárisan független, nulla vektorként ad vissza. A sajátvektorok és a sajátértékek együttesen is visszaadhatók az Eigensystem paranccsal.

Adott egy mátrix sajátvektorokkal , és , valamint a megfelelő sajátértékekkel , , és , akkor egy tetszőleges vektor felírható

(20)

A mátrix alkalmazása,

			(21)
			(22)

so

(23)

Ha , és , ebből következik, hogy

(24)

így a mátrix ismételt alkalmazása egy tetszőleges vektorra elképesztő módon a legnagyobb sajátértékkel rendelkező sajátvektorral arányos vektort eredményez.