mishadoff gondolatok

Mélység-első keresés megvalósítása a bináris fára verem és rekurzió nélkül.

Bináris fa tömb

Ez a bináris fa.

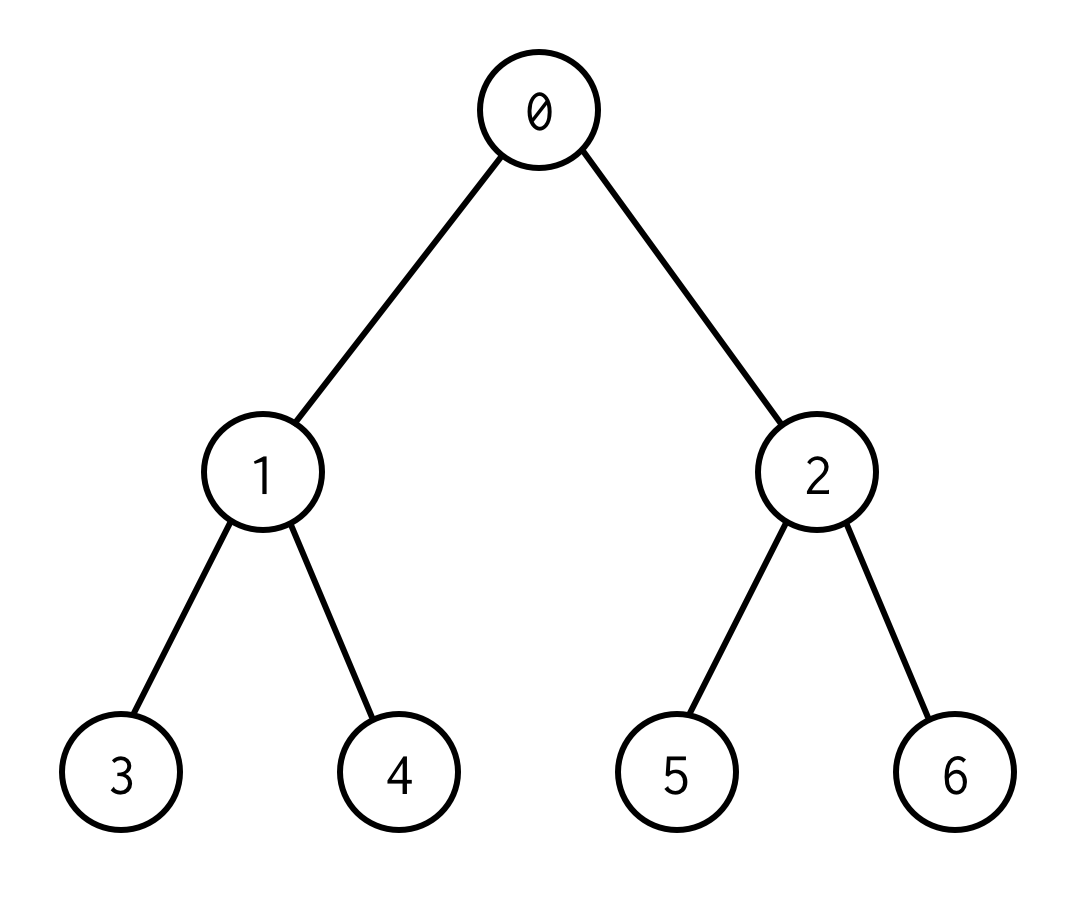
0 egy gyökércsomópont.
0 Két gyermeke van: bal 1 és jobb: 2.
Minden gyermekének vannak gyermekei és így tovább.
A gyermek nélküli csomópontok a levélcsomópontok (3,4,5,6).

A gyökér- és levélcsomópontok közötti élek száma határozza meg a fa magasságát.A fenti fa magassága 2.

A bináris fa implementálásának standard megközelítése a BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Mégis van egy trükk, amivel a bináris fát csak statikus tömbökkel lehet implementálni.Ha a bináris fa összes csomópontját nullától kezdve szintek szerint felsoroljuk, akkor azt tömbbe csomagolhatjuk.

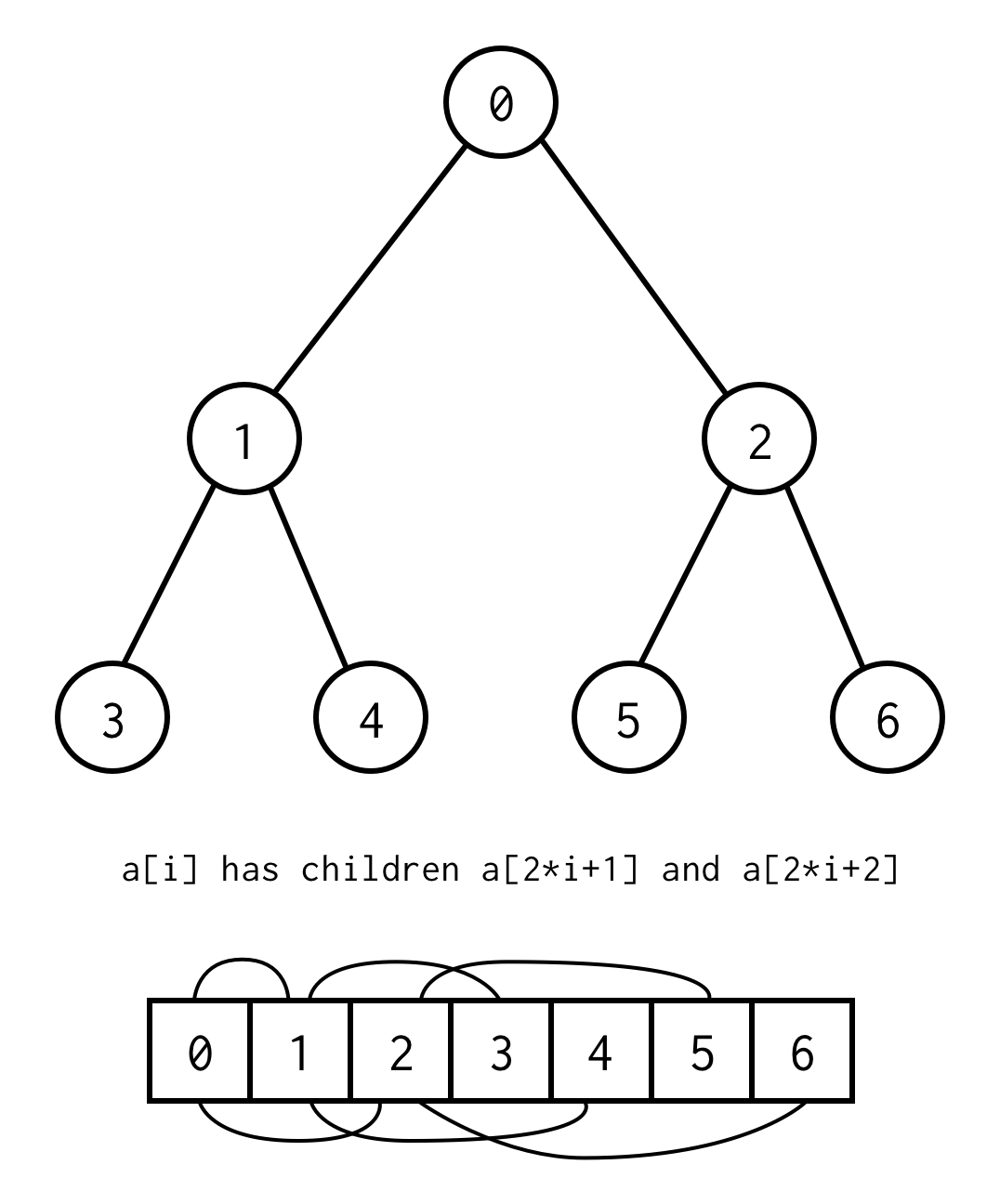
A szülő indexe és a gyermek indexe közötti kapcsolat,lehetővé teszi számunkra, hogy a szülőből a gyermekbe, valamint a gyermekből a szülőbe lépjünk

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Fontos megjegyzés, hogy a fának teljesnek kell lennie, ami azt jelenti, hogy az adott magassághoz pontosan elemeket kell tartalmaznia.

Ez a követelmény elkerülhető, ha a hiányzó elemek helyett null-t helyezünk el.A felsorolás továbbra is érvényes az üres csomópontokra is. Ennek le kell fednie minden lehetséges bináris fát.

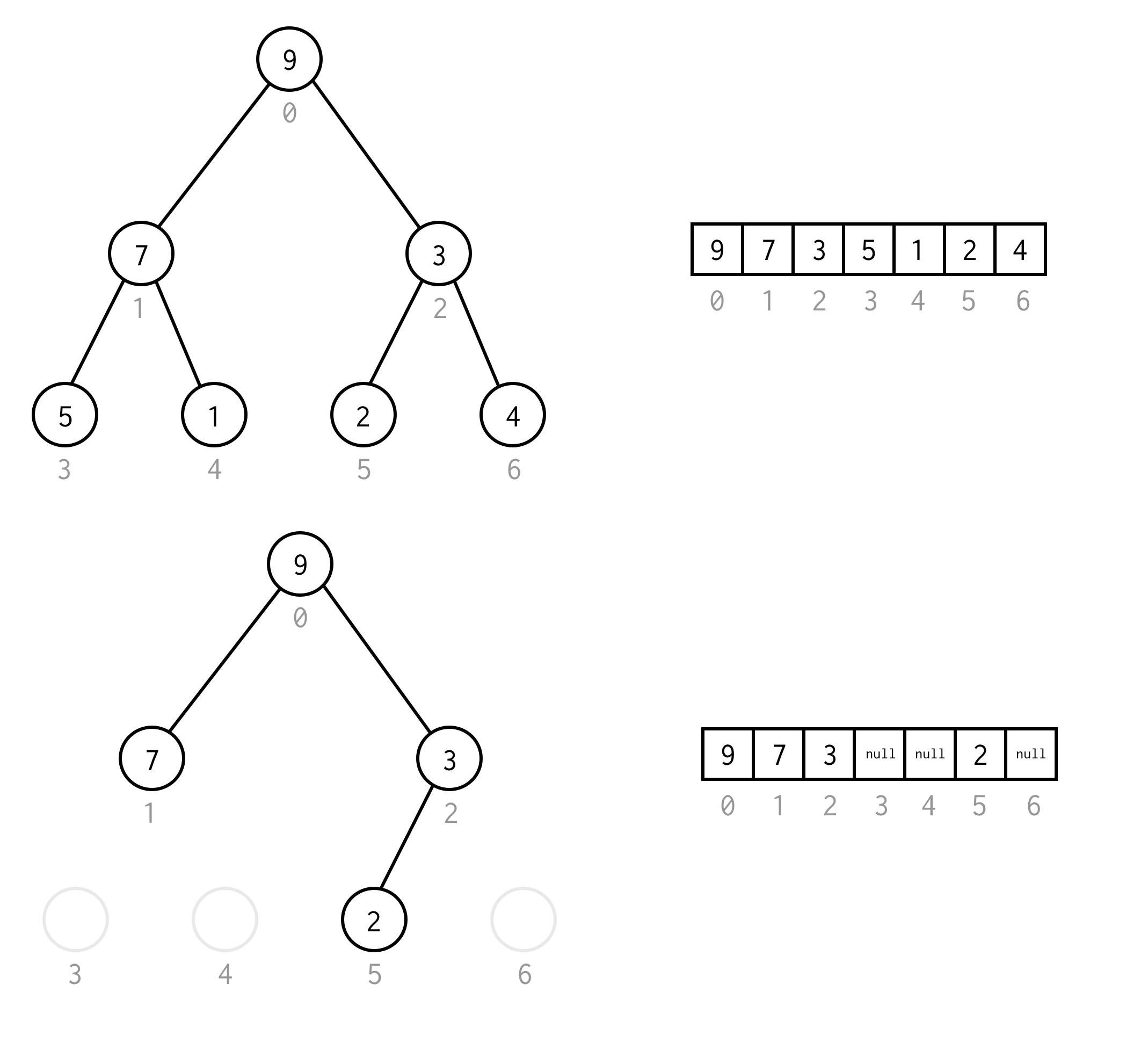
A bináris fa ilyen tömbi reprezentációját bináris fa tömbnek fogjuk nevezni.mindig feltételezzük, hogy tartalmazni fog elemeket.

BFS vs. DFS

A bináris fára két keresési algoritmus létezik:a szélesség-első keresés (BFS) és a mélység-első keresés (DFS).

A legjobb módja, hogy megértsük őket vizuálisan

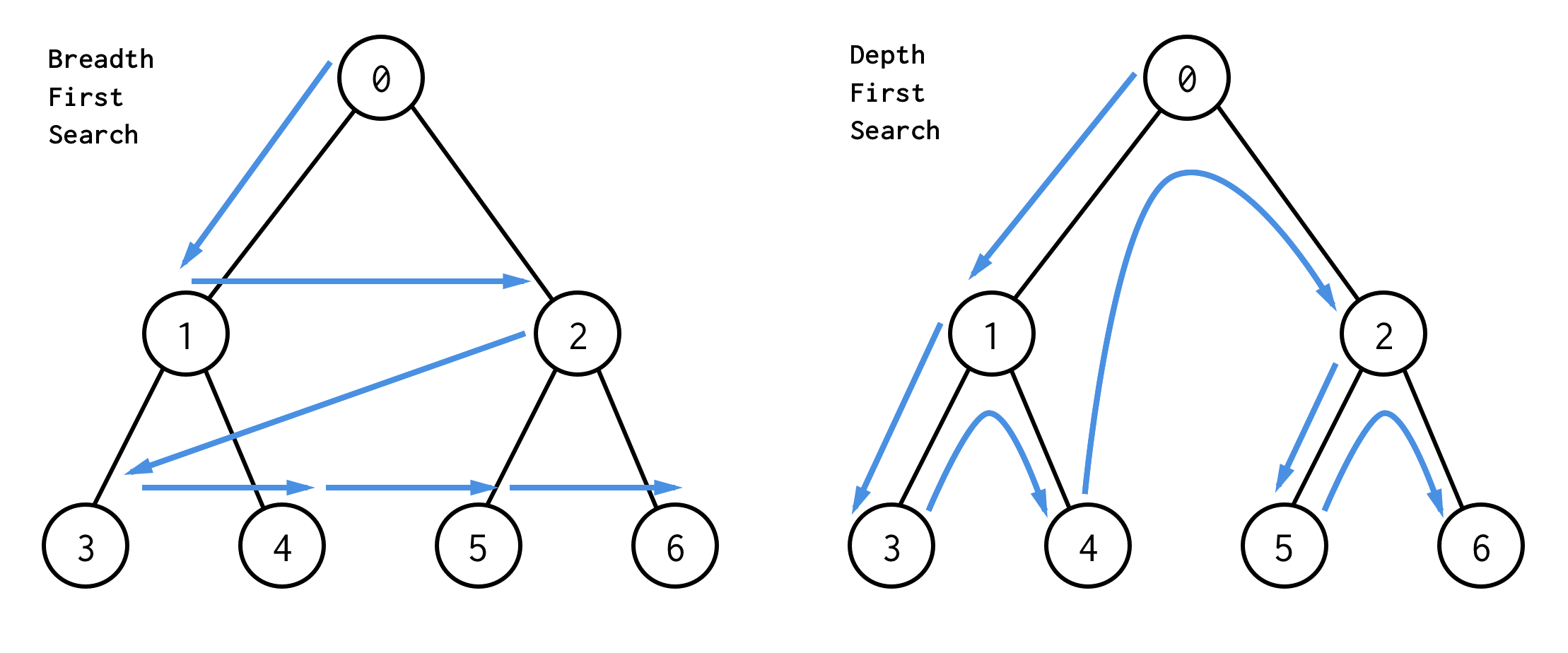
A BFS szintről szintre keresi a csomópontokat, a gyökércsomópontból kiindulva. Ezután ellenőrzi a gyermekeit. Aztán a gyerekeket a gyerekekre és így tovább.Amíg az összes csomópontot le nem dolgozzuk, vagy amíg meg nem találjuk a keresési feltételnek megfelelő csomópontot.

AzDFS másképp viselkedik. Az összes csomópontot ellenőrzi a gyökértől a levélig vezető bal oldali útvonaltól kezdve,majd felfelé ugrik és ellenőrzi a jobb oldali csomópontot és így tovább.

A klasszikus bináris fák esetében a BFS a Queue adatstruktúrával (LinkedList implements Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Ha a queue-t a veremmel helyettesítjük, akkor DFS implementációt kapunk.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Tegyük fel, hogy például a következő fában meg kell találnunk a 1 értékű csomópontot.

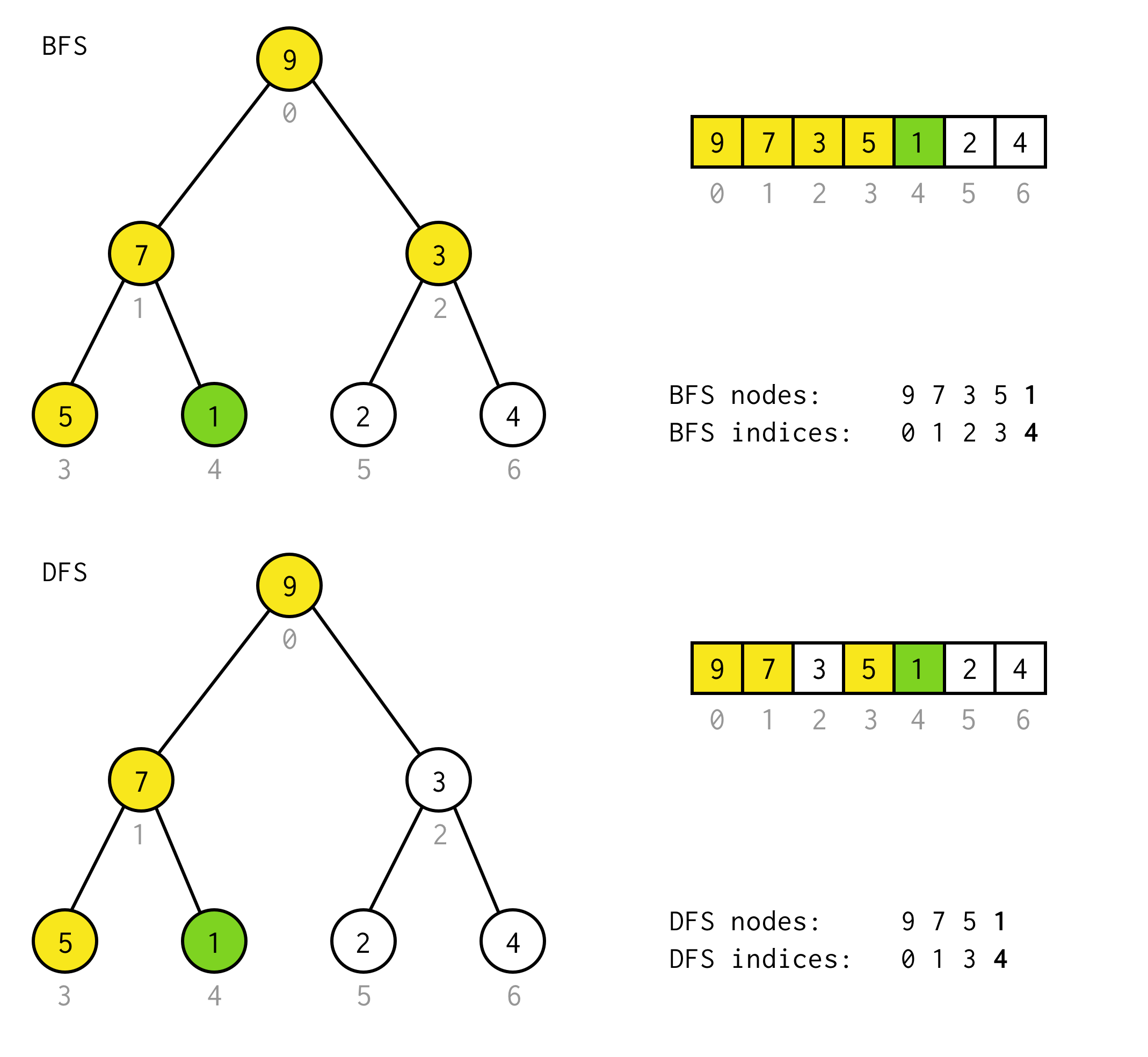
A sárga cellák azok a cellák, amelyeket a keresési algoritmus tesztel, mielőtt a szükséges csomópontot megtaláljuk.Vegyük figyelembe, hogy bizonyos esetekben a DFS kevesebb csomópontot igényel a feldolgozáshoz.Bizonyos esetekben több csomópontot igényel.

BFS és DFS bináris fa tömbhöz

A bináris fa tömb szélesség-első keresése triviális.Mivel a bináris fa tömb elemei szintenként vannak elhelyezve és abfs is szintenként ellenőrzi az elemeket, a bfs bináris fa tömbhöz csak lineáris keresés

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

A mélység-első keresés egy kicsit nehezebb.

A stack adatszerkezetet használva ugyanúgy megvalósítható, mint a klasszikus bináris fa esetében, csak az indexeket kell a stackbe tenni.

A rekurzió ebből a szempontból egyáltalán nem különbözik, csak az adatszerkezeti stack helyett implicit metódushívás stacket használunk.

Mi lenne, ha a DFS-t verem és rekurzió nélkül tudnánk megvalósítani.A végén csak a helyes index kiválasztása minden lépésnél?

Hát próbáljuk meg.

DFS bináris fa tömbhöz (verem és rekurzió nélkül)

Mint a BFS-ben is a gyökérindexből indulunk 0.
Aztán meg kell vizsgálnunk a baloldali gyermekét, amelynek indexét a 2*i+1 képlettel lehetne kiszámítani.
Hívjuk a következő baloldali gyermekhez való eljutás folyamatát duplázásnak.

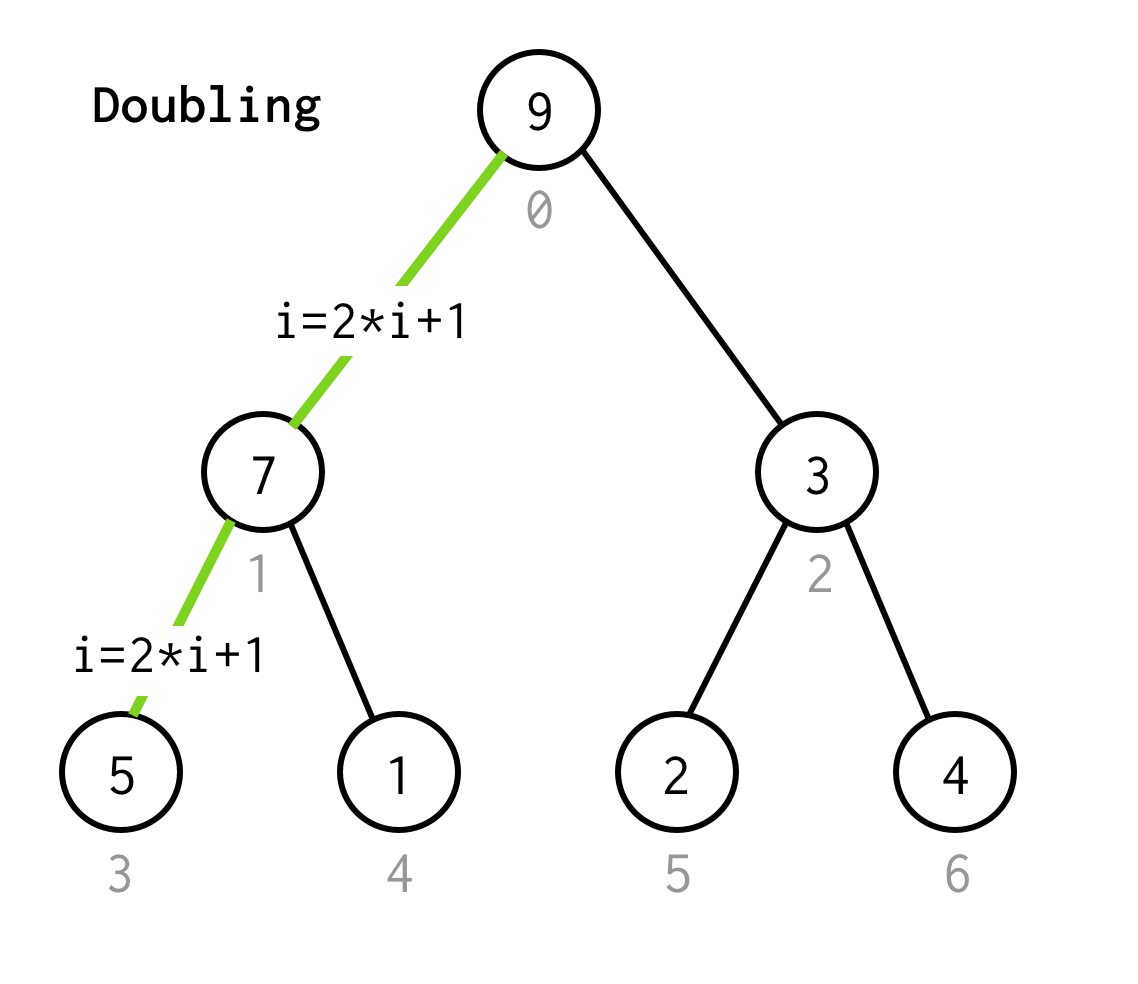
Folytatjuk az index duplázását, amíg meg nem állunk a levélcsomópontnál.

Hogyan értjük meg, hogy ez egy levélcsomópont?

Ha a következő baloldali gyermek index out of array bounds kivételt produkál, abba kell hagynunk a duplázást és a jobboldali gyermekre kell ugranunk.

Ez egy érvényes megoldás, de elkerülhetjük a felesleges duplázást.A megfigyelés itt az, hogy a fa elemeinek száma néhány height esetén kétszer nagyobb (és plusz egy)mint a fa height - 1 esetén.

A height = 2 fánál 7 elemünk van, a height = 3 fánál 7*2+1 = 15 elemünk van.

Ezt a megfigyelést felhasználva egyszerű feltételt

i < array.length / 2

Ezt a feltételt ellenőrizhetjük, hogy a fa bármely nem levél csomópontjára érvényes.

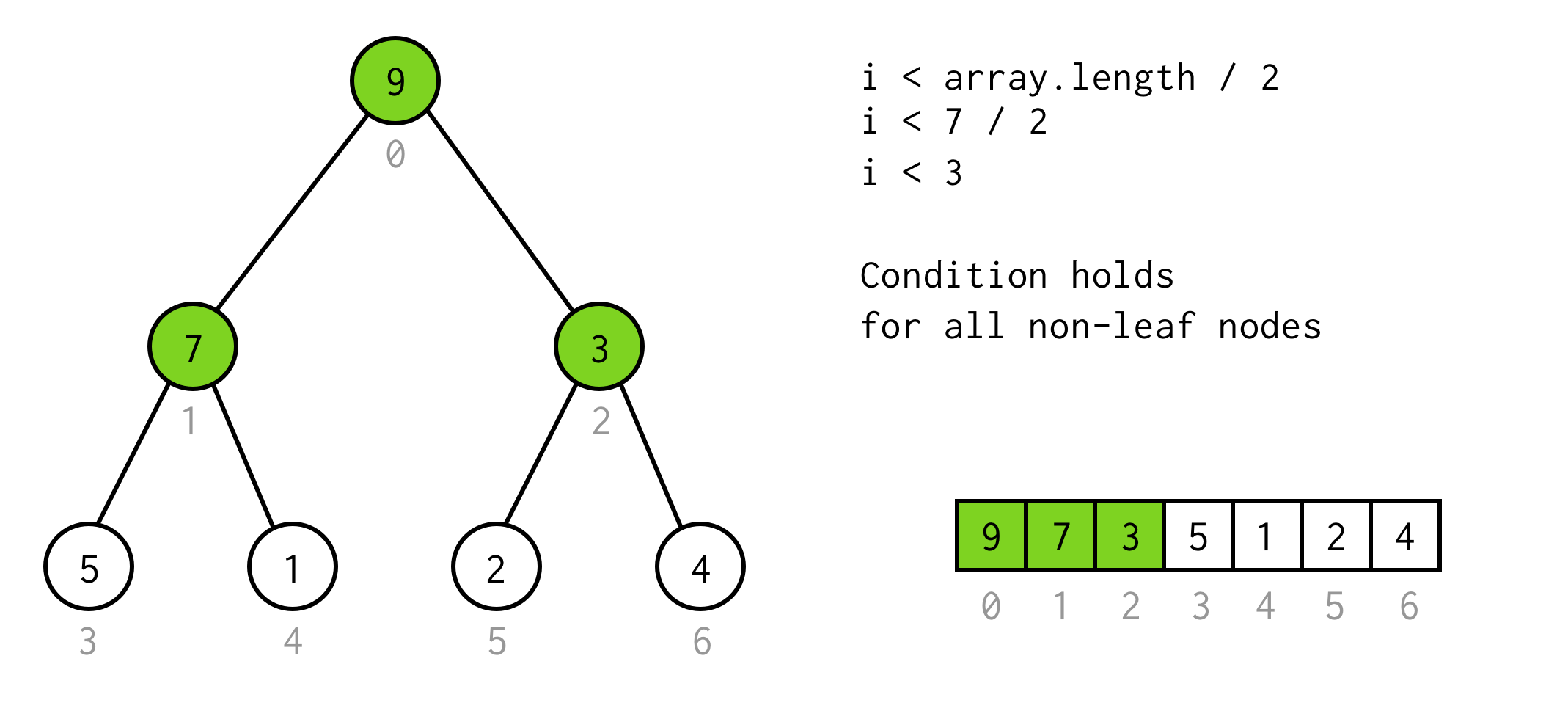
Eddig szép. Le tudjuk futtatni a duplázást, és még azt is tudjuk, hogy mikor kell abbahagyni. de így csak a csomópontok baloldali gyermekeit tudjuk ellenőrizni.

Ha megrekedtünk a levélcsomópontnál, és nem tudjuk tovább alkalmazni a duplázást, akkor ugrásműveletet végzünk.Alapvetően, ha a duplázás a bal gyermekhez megy, az ugrás a szülőhöz megy, és a jobb gyermekhez megy.

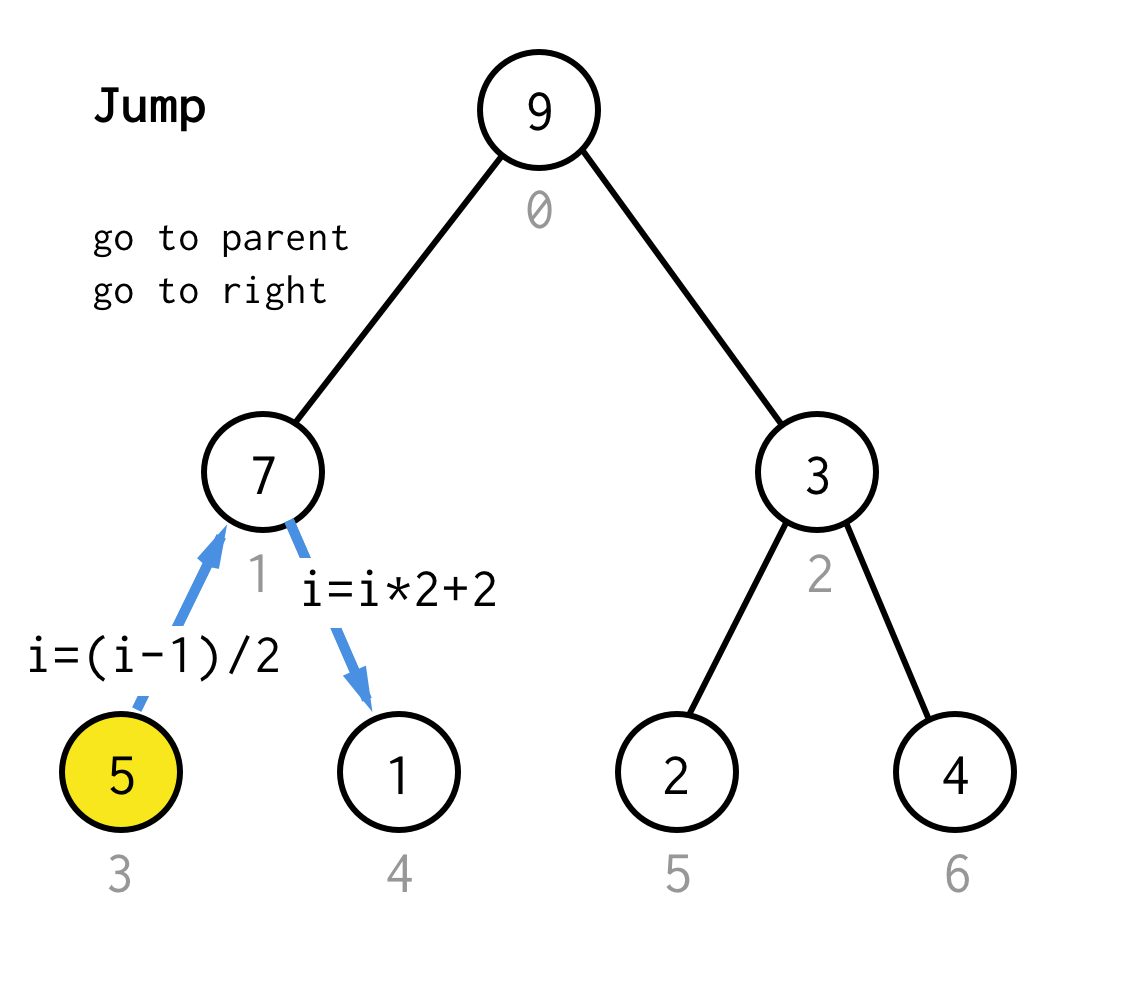
Az ilyen ugrás művelet megvalósítható a levélindex egyszerű növelésével.De amikor a következő levélcsomópontnál elakadunk, a növelés nem mozgatja a csomópontot a következő csomópontra, ami a DFS-hez szükséges.Ezért dupla ugrást kell végrehajtanunk

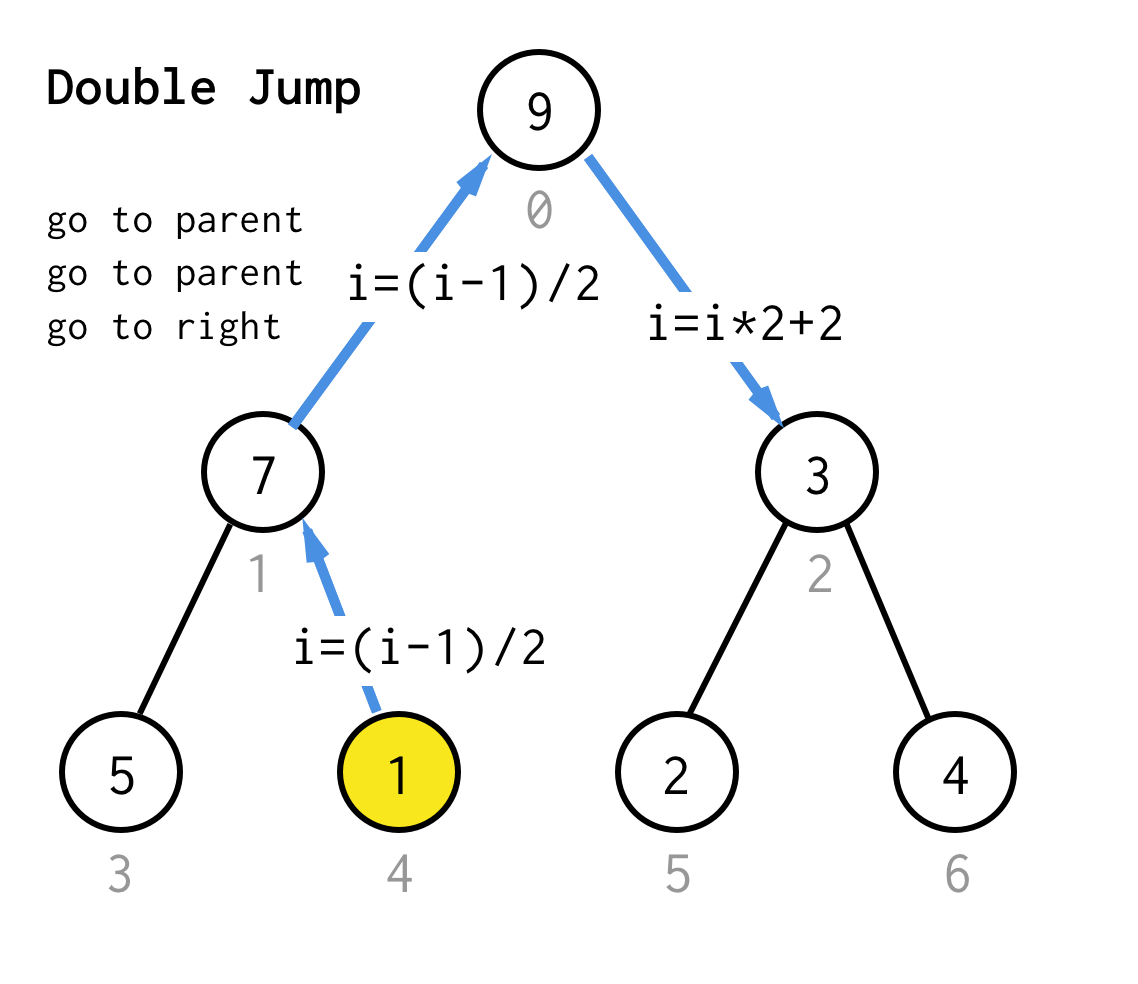
Az algoritmusunkhoz általánosabbá téve definiálhatjuk az ugrás N műveletet, amely megadja, hogy hány ugrás szükséges a szülőhöz, és mindig egy ugrással fejeződik be a megfelelő gyermekhez.

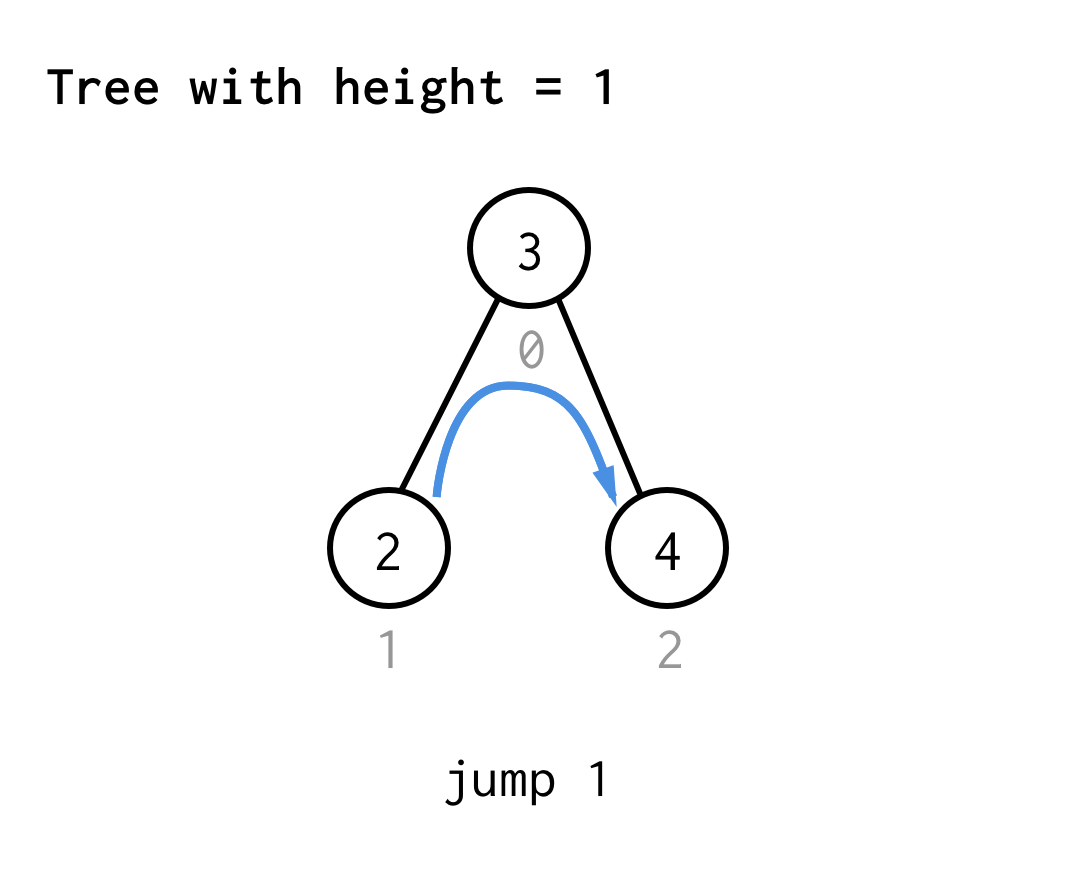
A 1 magasságú fához egy ugrás kell, az 1. ugrás

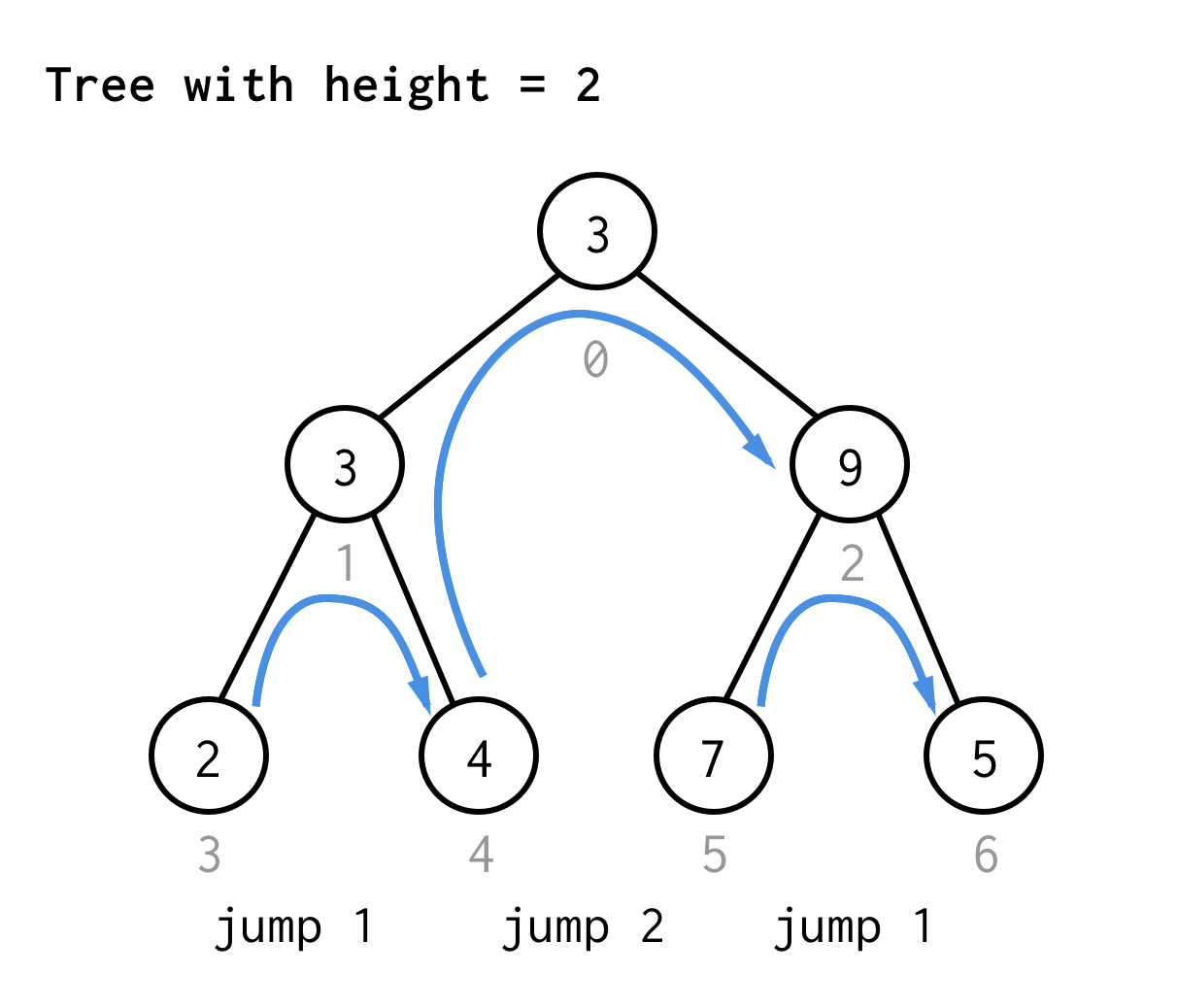
A 2 magasságú fához egy ugrás, egy dupla ugrás, majd ismét egy ugrás

A 3 magasságú fához ugyanezeket a szabályokat alkalmazva 7 ugrást kapunk.

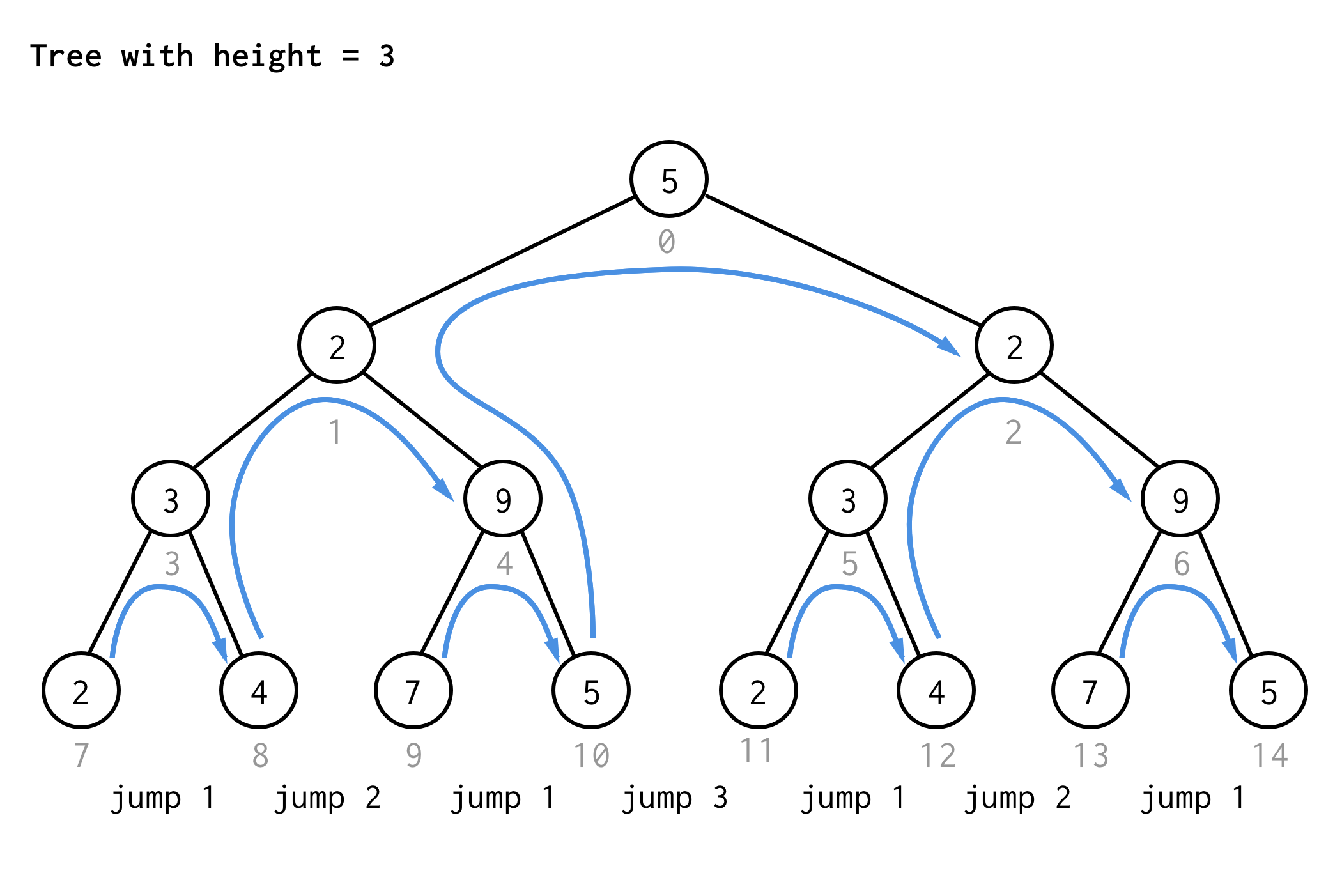
Látszik a minta?

Ha ugyanezt a szabályt alkalmazzuk a 4 magasságú fára, és csak az ugrásértékeket írjuk fel, akkor a következő sorszámot kapjuk

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Ezt a sorszámot Zimin szavaknak hívják, és rekurzív definíciója van,ami nem jó, mert nem szabad rekurziót használni.

Keresünk valami más módot a kiszámítására.

Ha figyelmesen megnézzük az ugrási szekvenciát, láthatjuk a nem rekurzív mintát.

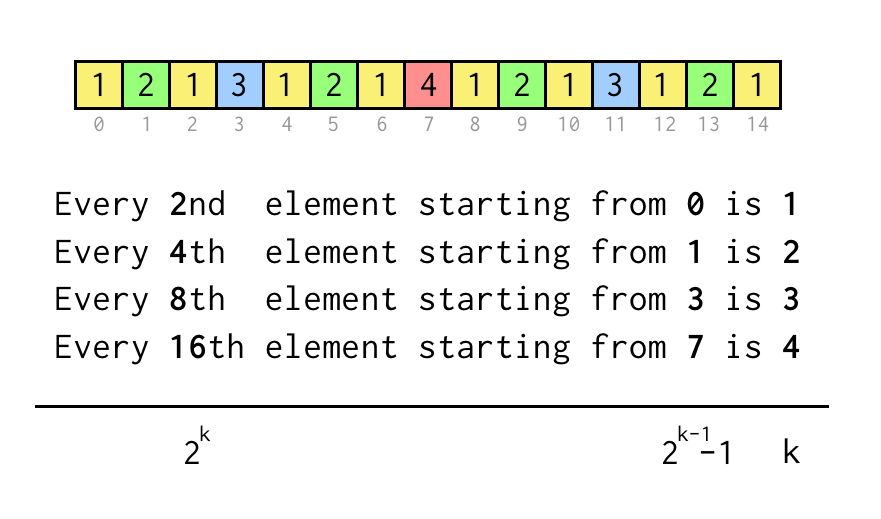
Az aktuális levél j indexét követhetjük, ami megfelel a fenti szekvencia tömb indexének.

Az olyan állítás ellenőrzéséhez, mint “Minden 8. elem 3-tól kezdődően”, csak ellenőrizzük j % 8 == 3,ha igaz, három ugrás a szükséges szülő csomópontra.

Iteratív ugrási folyamat a következő lesz

• Kezdjük k = 1
• Egyszer ugrunk a szülőhöz a i = (i - 1)/2
• alkalmazásával>Ha leaf % 2*k == k - 1 minden ugrást végrehajtottunk, kilépünk
• Máskülönben a k értékét 2*k-ra állítjuk és ismételjük.

Ha mindent összerakva, amit megbeszéltünk

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Kész. DFS bináris fa tömbhöz verem és rekurzió nélkül

Bonyolultság

A bonyolultság kvadratikusnak tűnik, mert van ciklus a ciklusban,de nézzük mi a valóság.

• A teljes csomópontok felére (n/2) duplázó stratégiát használunk, ami állandó O(1)
• A teljes csomópontok másik felére (n/2) levélugró stratégiát használunk.
• A levélugró csomópontok fele (n/4) csak egy szülői ugrást igényel, 1 iterációt. O(1)
• Ebből a fele (n/8) két ugrást, azaz 2 iterációt igényel. O(1)
• …
• Csak egy leveles ugró csomópont igényel teljes ugrást a gyökérhez, ami O(logN)
• Szóval, ha minden esetben O(1), kivéve egy esetben, ami O(logN), azt mondhatjuk, hogy az ugrás átlaga O(1)
• A teljes bonyolultság O(n)

Teljesítmény

Bár az elmélet jó, nézzük meg, hogyan működik ez az algoritmus a gyakorlatban, összehasonlítva másokkal.

Tesztelünk 5 algoritmust, a JMH segítségével.

• BFS bináris fán (összekapcsolt lista mint várólista)
• BFS bináris fa tömbön (lineáris keresés)
• DFS bináris fán (verem)
• DFS bináris fa tömbön (verem)
• Iteratív DFS bináris fa tömbön

Előre létrehoztunk egy fát és predikátumot használunk az utolsó csomópontra való illesztéshez,hogy mindig ugyanannyi csomópontot találjunk el minden algoritmus esetében.

Az eredmények

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Nyilvánvaló, hogy a BFS a tömbön nyer. Ez csak egy lineáris keresés, tehát ha a bináris fát tömbként tudod ábrázolni, akkor tedd meg.

Az iteratív DFS, amelyet az imént ismertettünk a cikkben, a 2második helyen végzett, és 4.5szer lassabb, mint a lineáris keresés (BFS tömbön)

A többi három algoritmus még lassabb, mint az iteratív DFS, valószínűleg azért, mert további adatstruktúrákat, extra helyet és memóriafoglalást igényelnek.

A legrosszabb eset pedig a BFS bináris fán. Gyanítom, hogy itt a linkelt lista a probléma.

Következtetés

A bináris fa tömb egy szép trükk a hierarchikus adatszerkezetek statikus tömbként való ábrázolására (összefüggő régió a memóriában). Egyszerű indexkapcsolatot definiál a szülőből a gyermekhez, valamint a gyermekből a szülőhöz való mozgáshoz, ami a klasszikus bináris tömbi reprezentációval nem lehetséges. Van néhány hátránya, mint például a lassú beszúrás/törlés, de biztos vagyok benne, hogy rengeteg alkalmazása van a bináris fa tömbnek.

Amint megmutattuk, a tömbökön végrehajtott keresési algoritmusok, a BFS és a DFS sokkal gyorsabbak, mint a referencia alapú struktúrán végrehajtott testvéreik. A való világ problémáihoz ez nem olyan fontos, és valószínűleg én továbbra is a referencia alapú bináris tömböt fogom használni.

Mindenesetre ez egy szép feladat volt. Várom a “DFS bináris tömbön rekurzió és verem nélkül” kérdést a következő interjún.

• algoritmusok
• adatstruktúrák
• programozás

mishadoff 2017. szeptember 10.