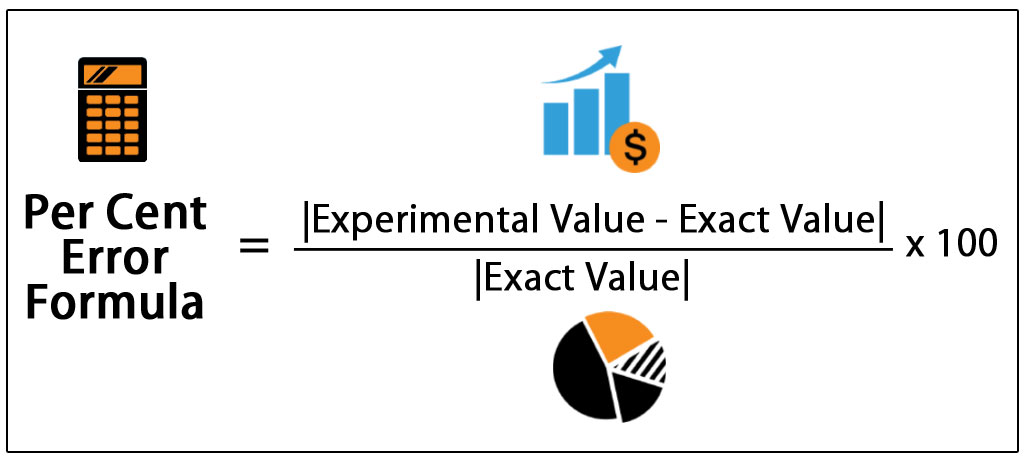
Vzorce pro výpočet procentní chyby

Vzorce pro výpočet procentní chyby

Vzorce pro výpočet procentní chyby se počítá jako rozdíl mezi odhadovaným a skutečným číslem ve srovnání se skutečným číslem a vyjadřuje se v procentech, jinými slovy je to prostě rozdíl mezi tím, co je skutečné číslo a předpokládané číslo v procentech.

V záležitostech souvisejících s vědou se často používá pojem vzorce procentuální chyby, v němž se má určit odchylka mezi experimentální hodnotou a přesnou hodnotou. Tento výpočet nám pomůže při porovnávání hodnoty, která je odvozena z experimentu, s přesnou nebo skutečnou hodnotou. Procentuální chyba také poskytuje informaci o tom, jak blízko je měření nebo odhad skutečné nebo reálné hodnotě.

Kroky výpočtu procentní chyby

Pro výpočet procentní chyby lze postupovat podle následujících kroků:

• Krok 1: Nejprve je třeba získat experimentální (předpokládanou) hodnotu a přesnou hodnotu.
• Krok 2: Zjistíme rozptyl mezi nimi a poté vezmeme absolutní hodnotu; to znamená, že je třeba ignorovat případné záporné znaménko. Tato hodnota se nazývá chyba.
• Krok 3: Dále zjistíme absolutní hodnotu přesné nebo skutečné hodnoty.
• Krok 4: Absolutní chybu (nezápornou), která byla určena v kroku 2, vydělíme absolutní skutečnou hodnotou nebo přesnou hodnotou.
• Krok 5: Nyní konečně vynásobíme výsledek, který jsme získali v kroku 4, číslem 100, takže výsledek převedeme na procentuální hodnotu a k výsledku přidáme symbol „%“.

Příklady

Příklad č. 1

V indickém Gudžarátu nedávno vzniklo nové turistické místo Socha jednoty a odhadovalo se, že v den jeho slavnostního otevření se kolem něj otočí asi 3 00 000 lidí. Přesný počet lidí, kteří přišli na její inauguraci, však byl asi 2 88 000. Je třeba vypočítat procentuální chybu.
Níže jsou uvedeny údaje pro výpočet procentní chyby

Výpočet procentní chyby bude tedy následující,

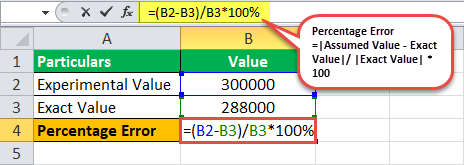
=(300000-288000)/288000*100

Procentní chyba bude –

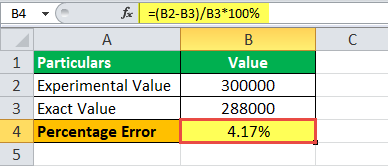
Percentní chyba= 4,17%

Příklad č. 2

Maloobchodní společnost Avenue Supermarket, působící pod názvem „Dmart“, je ve fázi expanze a společnost plánuje otevřít nové pobočky v nových městech. Na začátku účetního roku společnost plánovala a odhadovala otevření 24 poboček, nicméně do konce roku; společnost otevřela pouze 21 prodejen. Společnost se na vás obrátila, abyste vypočítali procentuální chybu, které se dopustila při počátečním plánování.

Níže jsou uvedeny údaje pro výpočet procentní chyby

Výpočet procentní chyby tedy bude následující,

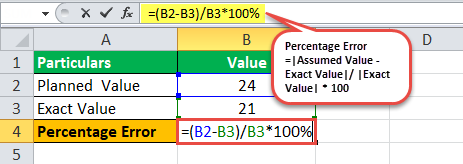
=(24-21)/21*100

Procentní chyba bude –

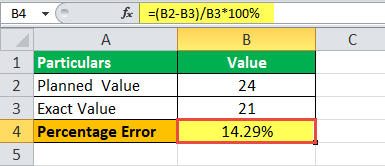
Procentní chyba= 14,29%

Příklad č. 3

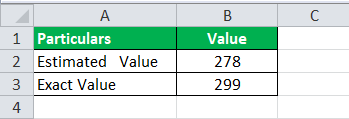
Podle průzkumu veřejného mínění, který provedl zpravodajský kanál během volební kampaně, kde odhadoval pro stranu XYZ zisk 278 křesel z 350 křesel. Po zveřejnění výsledků se ukázalo, že strana XYZ dokázala získat 299 mandátů z 350 mandátů. Zpravodajský kanál je skutečným výsledkem zmaten a nyní chce vědět, jakou chybu v rozpětí udělali a o kolik se zpozdili. Vypočítejte procentuální chybu.

Níže jsou uvedeny údaje pro výpočet procentuální chyby.

Výpočet procentuální chyby bude tedy následující,

Procentní chyba bude –

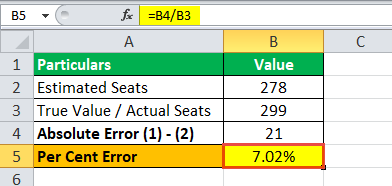
Procentní chyba=-7,02%

Toto byl průvodce vzorcem procentuální chyby. Dozvíme se zde, jak vypočítat Procentní chybu pomocí jejího vzorce s praktickými příklady a šablonou Excelu ke stažení. Více informací o financování se můžete dozvědět z následujících článků –

• Rozmezí chyby
• Vzorce multiplikátoru
• Procentní změna v Excelu
• Vzorec Intervalu spolehlivosti
• APR vs APY

.