Vlastnosti úhlů trojúhelníku

Související témata:
Další lekce geometrie
Pracovní listy z geometrie
Geometrické hry
V těchto lekcích si shrneme vlastnosti úhlů trojúhelníku.

• Věta o součtu úhlů trojúhelníku – Součet 3 úhlů v trojúhelníku je vždy 180°
• Součet vnitřního úhlu a k němu přilehlého vnějšího úhlu je 180°
• Věta o vnějším úhlu – Vnější úhel trojúhelníku je roven součtu dvou protilehlých vnitřních úhlů
• Rovnostranný trojúhelník má 3 stejné úhly, z nichž každý má 60°. Rovnoramenný trojúhelník má 2 stejné úhly, které jsou úhly opačnými ke 2 stejným stranám

Úhly trojúhelníku mají následující vlastnosti:

Vlastnost 1: Věta o součtu úhlů v trojúhelníku

Součet 3 úhlů v trojúhelníku je vždy 180°.

Příklad :

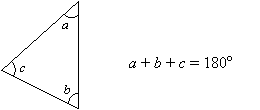
Jak dokázat větu o součtu trojúhelníků?
Následující video ukazuje, jak dokázat, že součet úhlů v trojúhelníku je 180°. (Triangle Sum Theorem)

• Ukázat řešení krok za krokem

Jak najít chybějící úhel v trojúhelníku pomocí věty o součtu trojúhelníků?
Krok 1: Napište rovnici tak, že sečtete všechny úhly a dáte jim hodnotu 180°.
Krok 2: Vyřeš x.
Krok 3: Substitucí najdi chybějící úhly.

• Ukázat řešení krok za krokem

Vlastnost 2:

Součet vnitřního úhlu a jeho sousedního vnějšího úhlu je 180°.

Příklad :

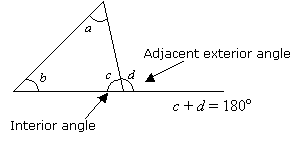
Vlastnost 3: Věta o vnějších úhlech

Vnější úhel trojúhelníku je roven součtu dvou protilehlých vnitřních úhlů.

Příklad :

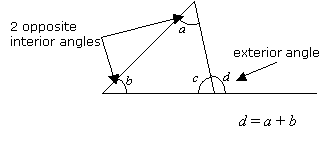
Vnější úhly trojúhelníku
Zjištění neznámého úhlu trojúhelníku
Příklad:
1. Vyhodnoťte trojúhelník abc, kde a = 40° a b = 60°. Jaký je vnější úhel k ∠acb?“
2. Vyhodnoťte trojúhelník abc, kde a = 50° a b = 30°. Jaký je vnější úhel k ∠acb?
2. Vyhodnoťte trojúhelník abc, kde a = 90° a b = 40°. Jaký je vnější úhel k ∠acb?“

• Ukázat postupná řešení

Jak použít větu o vnějším úhlu k řešení úloh týkajících se úhlů v trojúhelníku?“

• Ukázat postupná řešení

Vlastnost 4:

Rovnostranný trojúhelník má 3 stejné úhly, z nichž každý má 60°.
Rovnoramenný trojúhelník má 2 stejné úhly, což jsou úhly opačné ke 2 stejným stranám.
Jak najít chybějící úhel v rovnoramenném trojúhelníku?“

• Ukázat postupná řešení

Rovnoběžky a věta o součtu úhlů v trojúhelníku

• Ukázat postupná řešení

Výše uvedené vlastnosti úhlů nám mohou pomoci najít neznámé úhly v trojúhelníku.

Příklad:

Najděte hodnotu x v následujícím trojúhelníku.

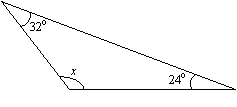
Řešení:

x + 24° + 32° = 180° (součet úhlů je 180°)
x + 56° = 180°
x = 180° – 56° = 124°

Příklad :

Najděte hodnoty x a y v následujícím trojúhelníku.

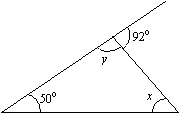
Řešení:

x + 50° = 92° (součet protilehlých vnitřních úhlů = vnější úhel)
x = 92° – 50° = 42°

y + 92° = 180° (vnitřní úhel + přilehlý vnější úhel = 180°.)
y = 180° – 92° = 88°

Vyzkoušejte níže uvedenou bezplatnou kalkulačku a řešitele úloh Mathway k procvičení různých matematických témat. Vyzkoušejte si uvedené příklady nebo zadejte vlastní úlohu a zkontrolujte si odpověď pomocí vysvětlení krok za krokem.

.