Vlastní vektor

Vlastní vektory jsou speciální množinou vektorů spojených s lineárním systémem rovnic (tj.e., maticovou rovnicí), které se někdy nazývají také charakteristické vektory, vlastní vektory nebo skryté vektory (Marcus a Minc 1988, s. 144).

Určení vlastních vektorů a vlastních hodnot systému je nesmírně důležité ve fyzice a technice, kde je ekvivalentní diagonalizaci matic a objevuje se v takových běžných aplikacích, jako je analýza stability, fyzika rotujících těles a malých kmitů vibračních systémů, abychom jmenovali jen některé. Každý vlastní vektor je spárován s odpovídajícím tzv. vlastním číslem. Z matematického hlediska je třeba rozlišovat dva různé druhy vlastních vektorů: levé vlastní vektory a pravé vlastní vektory. Pro mnoho problémů ve fyzice a technice však stačí uvažovat pouze pravé vlastní vektory. Termín „vlastní vektor“ používaný v takových aplikacích bez výhrad lze proto chápat jako označení pravého vlastního vektoru.

Rozklad čtvercové matice na vlastní čísla a vlastní vektory je v této práci znám jako vlastní rozklad a skutečnost, že tento rozklad je vždy možný, pokud je matice složená z vlastních vektorů čtvercová, je známa jako věta o vlastním rozkladu.

Definice pravého vlastního vektoru jako sloupcového vektoru splňujícího

(1)

kde je matice, takže

(2)

což znamená, že pravá vlastní čísla musí mít nulový determinant, tj.e.,

(3)

Podobně definujeme levý vlastní vektor jako řádkový vektor splňující

(4)

Při transpozici každé strany dostaneme

(5)

který lze přepsat jako

(6)

Znovu uspořádejte, abyste získali

(7)

což znamená

(8)

Přepisem dostaneme

			(9)
			(10)
			(11)

kde poslední krok vyplývá z identity

(12)

Vyrovnání rovnic (◇) a (11), které jsou obě rovny 0 pro libovolné a , tedy vyžaduje, aby , tj, levá a pravá vlastní čísla jsou ekvivalentní, což je tvrzení, které neplatí pro vlastní vektory.

Nechť je matice tvořená sloupci pravých vlastních vektorů a je matice tvořená řádky levých vlastních vektorů. Nechť

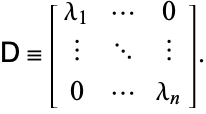(13)

Tak

.

			(14)
			(15)

a

			(16)
			(17)

takže

(18)

Ale tato rovnice má tvar

.

(19)

kde je diagonální matice, musí tedy platit, že je také diagonální. Zejména je-li symetrická matice, pak levý a pravý vlastní vektor jsou prostě vzájemnou transpozicí, a je-li samodružná matice (tj. je hermitovská), pak levý a pravý vlastní vektor jsou adjungované matice.

Vlastní vektory nemusí být rovny nulovému vektoru. Nenulový skalární násobek vlastního vektoru je ekvivalentní původnímu vlastnímu vektoru. Proto se bez ztráty obecnosti vlastní vektory často normalizují na jednotkovou délku.

Ačkoli matice má vždy vlastních hodnot, z nichž některé nebo všechny mohou být degenerované, může mít taková matice 0 až lineárně nezávislých vlastních vektorů. Například matice má pouze jediný vlastní vektor .

Vlastní vektory lze ve Wolframově jazyce vypočítat pomocí funkce Eigenvectors. Tento příkaz vždy vrací seznam délky , takže všechny vlastní vektory, které nejsou lineárně nezávislé, jsou vráceny jako nulové vektory. Vlastní vektory a vlastní hodnoty lze vrátit společně pomocí příkazu Eigensystem.

Dáno matice s vlastními vektory , a a odpovídajícími vlastními hodnotami , a , pak libovolný vektor lze zapsat

(20)

Při použití matice ,

			(21)
			(22)

tak

(23)

Jestliže a , vyplývá z toho, že

(24)

takže opakovaná aplikace matice na libovolný vektor úžasně vede ina vektor úměrný vlastnímu vektoru s největší vlastní hodnotou.