Ochrana osobních údajů & Cookies
Tato stránka používá cookies. Pokračováním souhlasíte s jejich používáním. Zjistěte více, včetně toho, jak cookies ovládat.
Spirála je křivka, která „vychází z bodu a při otáčení kolem bodu se vzdaluje“.

Existuje mnoho různých typů spirál v závislosti na vzorcích, které je vytvářejí. V tomto příspěvku se budu zabývat dvourozměrnými spirálami (všimněte si, že existují také různé trojrozměrné spirály).
Archimédova spirála
Jedná se o spirálu pojmenovanou po slavném řeckém matematikovi Archimédovi, který ji jako první popsal ve své knize O spirálách. Je popsána následující polární rovnicí:
kde a a b jsou reálná čísla.
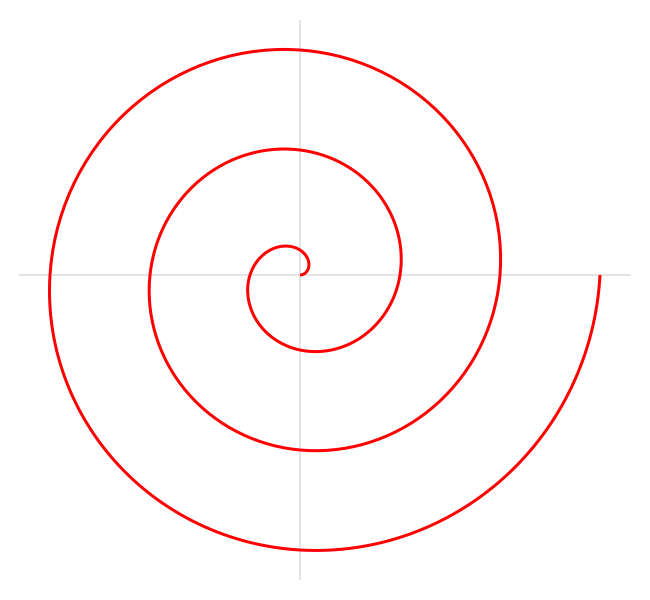
Změnou parametru a se bude spirála otáčet a parametr b řídí vzdálenost mezi po sobě jdoucími otáčkami.
Fermatova spirála
Fermatova spirála je parabolická spirála, která se řídí následující polární rovnicí:
Jedná se o typ Archimédovy spirály.

Eulerova spirála
Známá také jako Cornuova spirála, je to křivka, jejíž křivost roste s rostoucí vzdáleností od počátku; „křivost kruhové křivky je rovna reciprokému poloměru“.

Parametrický tvar se skládá ze dvou rovnic s Fresnelovými intervaly, které lze řešit pouze přibližně.
Tyto integrály, a tedy i Eulerovu spirálu, lze použít k popisu rozložení energie Fresnelovy difrakce na jedné štěrbině ve vlnové teorii.
Hyperbolická spirála
Hyperbolická spirála, kterou poprvé navrhl Pierre Varignon v roce 1704, je transcendentální křivka, což znamená, že „je to analytická funkce, která nesplňuje polynomickou rovnici“. Je opakem archimédovské spirály a má tedy následující polární rovnici:
Ve středu je v nekonečné vzdálenosti od pólu; pro θ začínající v 0 začíná r v nekonečnu.
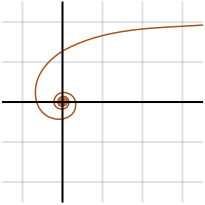
Lituus
Lituus je spirála s polární rovnicí:
kde k je konstanta. Úhel je tedy nepřímo úměrný čtverci poloměru. 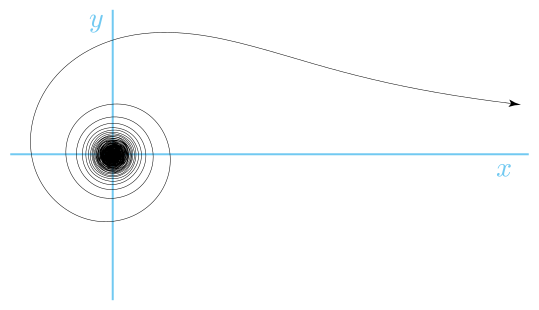
Křivka byla pojmenována podle starořímské lituy (zakřivené augurální hole nebo válečné trubky) Rogerem Cotesem ve sborníku prací publikovaném v roce 1722.
Logaritmická spirála
 Logaritmická spirála je samopodobná spirála, která se často vyskytuje v přírodě. Poprvé ji popsal Descartes, ale podrobně ji studoval Jacob Bernoulli, který ji nazval „podivuhodnou spirálou“. Její polární rovnice je
Logaritmická spirála je samopodobná spirála, která se často vyskytuje v přírodě. Poprvé ji popsal Descartes, ale podrobně ji studoval Jacob Bernoulli, který ji nazval „podivuhodnou spirálou“. Její polární rovnice je





Napsat komentář