mishadoffovy myšlenky

Implementace prohledávání do hloubky pro binární strom bez zásobníku a rekurze.

Pole binárních stromů

Toto je binární strom.

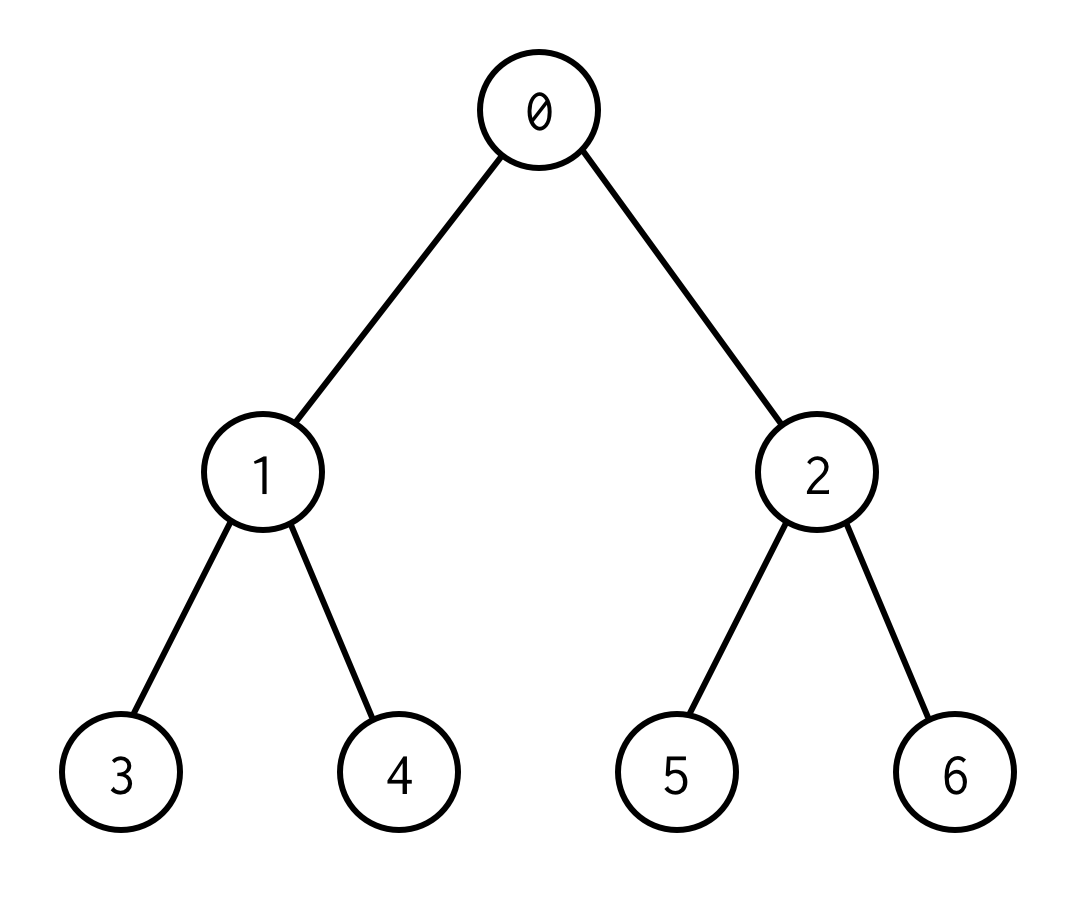
0 je kořenový uzel.
0 má dva potomky: levého 1 a pravého: 2.
Každý z jeho potomků má své potomky atd.
Uzly bez potomků jsou listové uzly (3,4,5,6).

Počet hran mezi kořenovými a listovými uzly určuje výšku stromu.Výše uvedený strom má výšku 2.

Standardní přístup k implementaci binárního stromu je definovat třídu s názvem BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Existuje však trik, jak implementovat binární strom pouze pomocí statických polí. pokud vyjmenujete všechny uzly binárního stromu podle úrovní počínaje nulou, můžete je zabalit do pole.

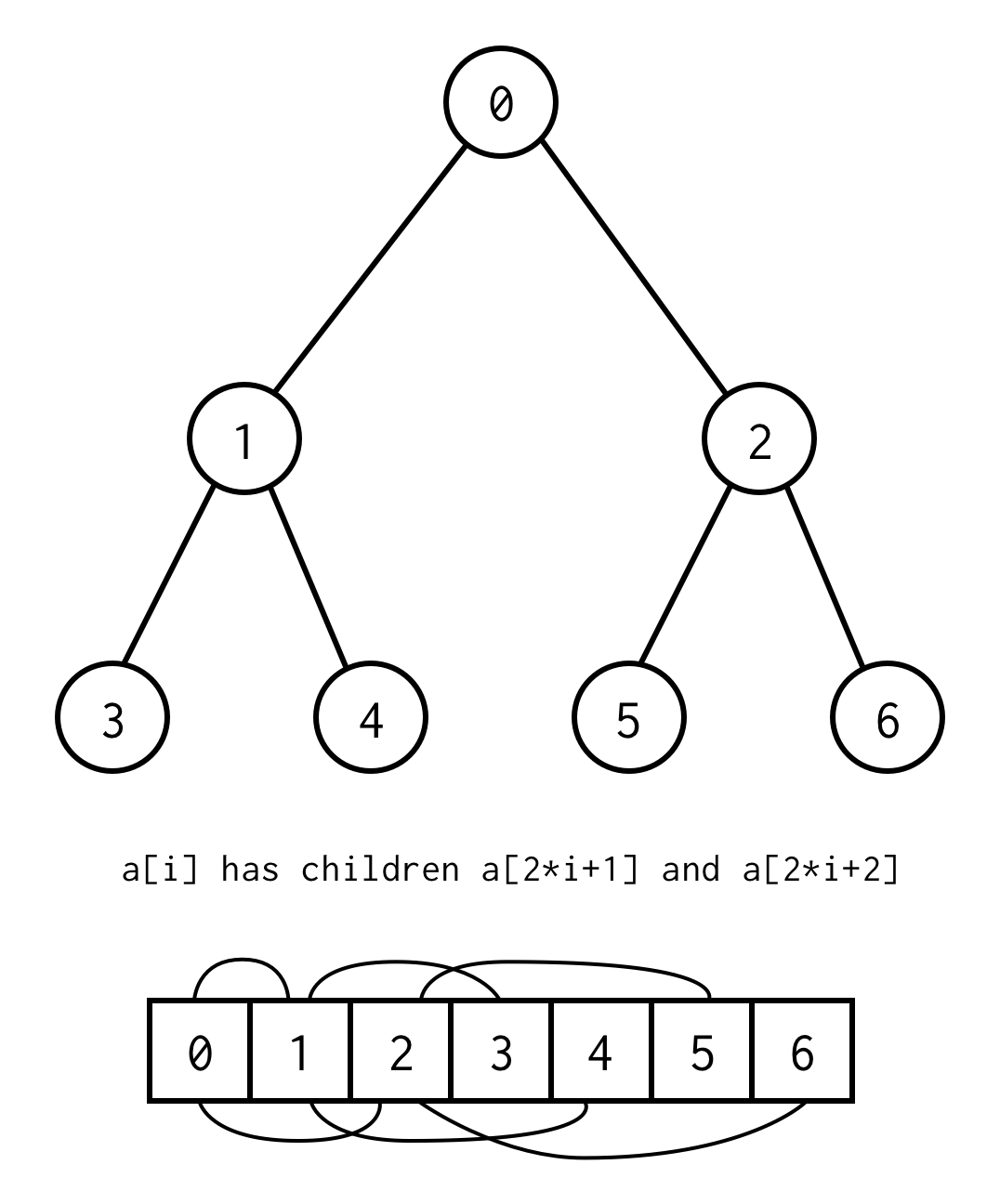
Vztah mezi indexem rodiče a indexem dítěte,nám umožní přecházet z rodiče na dítě, stejně jako z dítěte na rodiče

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Důležité upozornění, že strom by měl být úplný, což znamená, že pro danou výšku by měl obsahovat přesně prvky.

Takovému požadavku se můžete vyhnout tak, že místo chybějících prvků umístíte nullVýčet stále platí i pro prázdné uzly. To by mělo pokrýt všechny možné binární stromy.

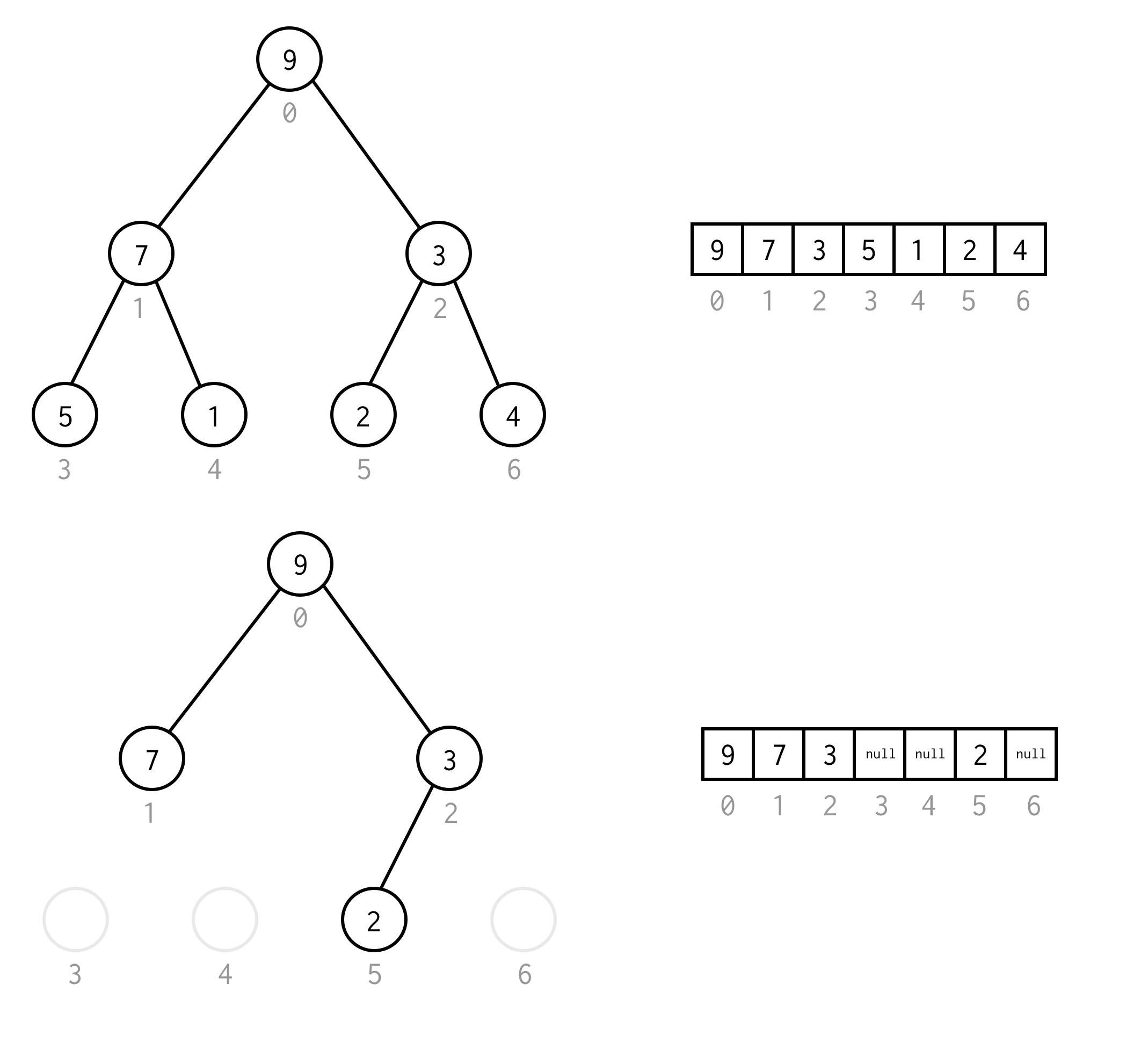
Takovou reprezentaci pole pro binární strom budeme nazývat pole binárního stromu. vždy předpokládáme, že bude obsahovat prvky.

BFS vs DFS

Pro binární strom existují dva prohledávací algoritmy:prohledávání podle šířky (BFS) a prohledávání podle hloubky (DFS).

Nejlépe je pochopíme vizuálně

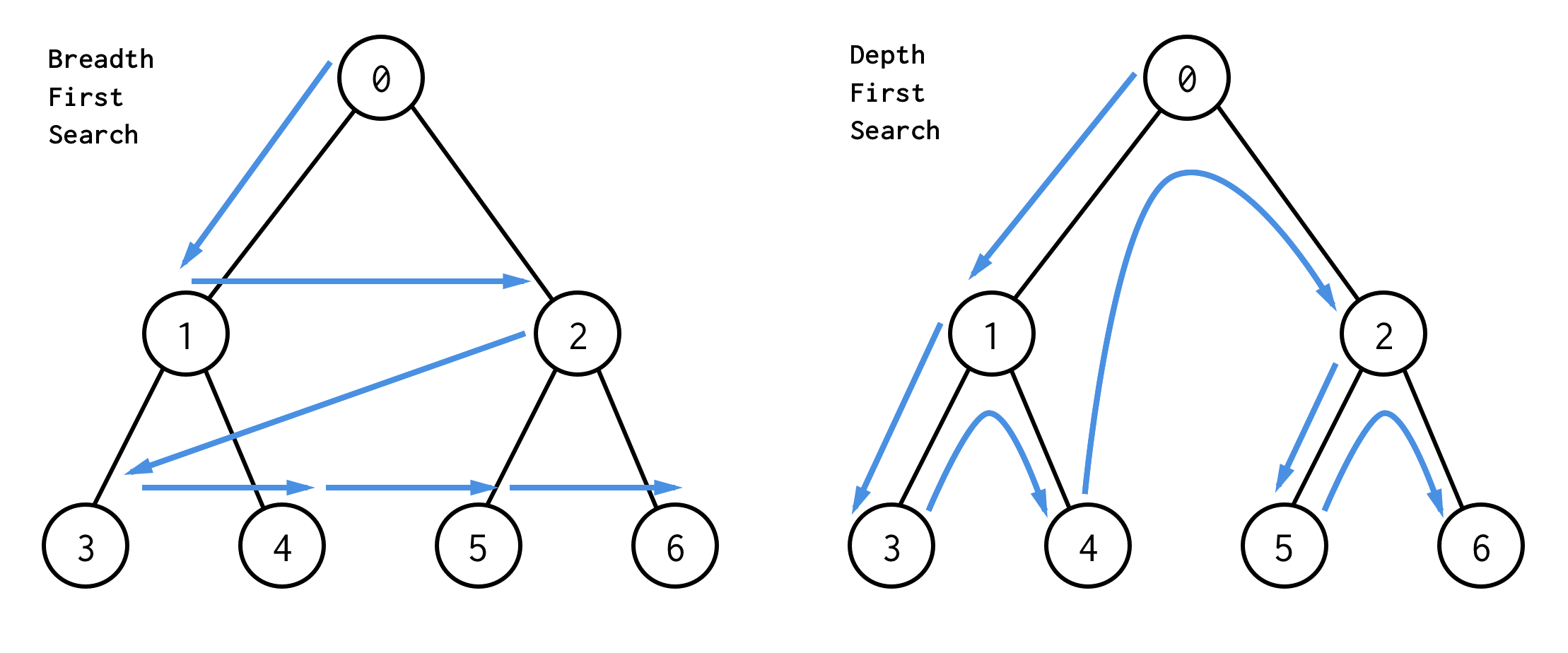
BFS prohledává uzly po úrovních, počínaje kořenovým uzlem. Poté kontroluje jeho potomky. Pak děti pro děti a tak dále. dokud nejsou zpracovány všechny uzly nebo není nalezen uzel, který splňuje podmínku hledání.

DFS se chová jinak. Kontroluje všechny uzly od nejlevější cesty od kořene k listu, pak skočí nahoru a kontroluje pravý uzel a tak dále.

Pro klasické binární stromy je BFS implementován pomocí datové struktury Queue (LinkedList implementuje Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Pokud nahradíte frontu zásobníkem, dostanete implementaci DFS.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Předpokládejme, že v následujícím stromu potřebujete najít uzel s hodnotou 1.

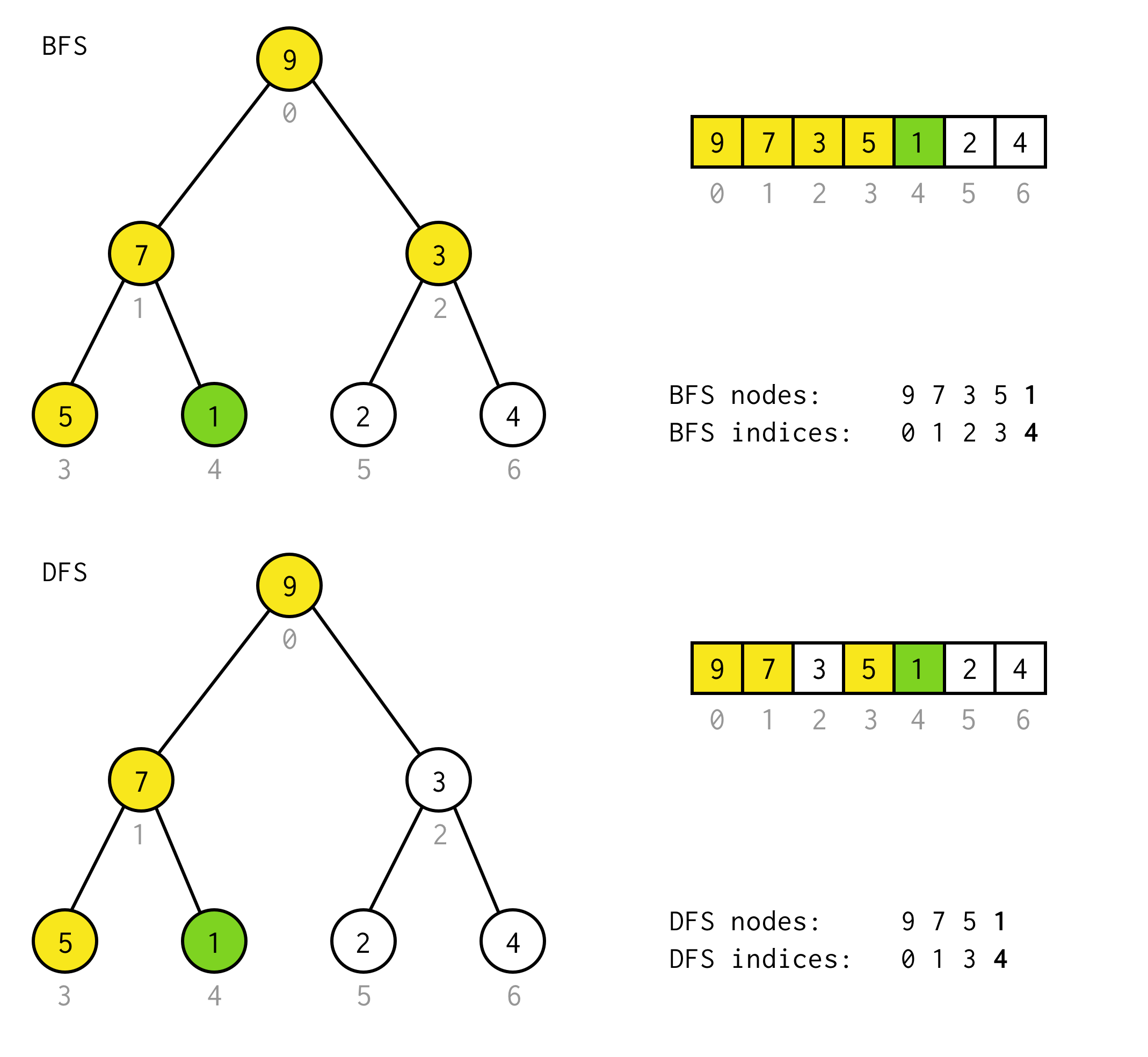
Žluté buňky jsou buňky, které jsou testovány v algoritmu vyhledávání před nalezením potřebného uzlu. berte v úvahu, že pro některé případy DFS potřebuje ke zpracování méně uzlů.Pro některé případy vyžaduje více.

BFS a DFS pro binární stromové pole

Vyhledávání podle šířky pro binární stromové pole je triviální. protože prvky v binárním stromovém poli jsou umístěny po úrovních abfs také kontroluje prvky po úrovních, je bfs pro binární stromové pole jen lineární vyhledávání

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

Vyhledávání podle hloubky je o něco těžší.

Při použití zásobníkové datové struktury by se to dalo implementovat stejně jako u klasického binárního stromu, jen se do zásobníku vloží indexy.

Z tohoto hlediska se rekurze vůbec neliší, jen se místo zásobníku datové struktury použije implicitní zásobník volání metod.

Co kdybychom mohli implementovat DFS bez zásobníku a rekurze.Nakonec jde jen o výběr správného indexu na každém kroku?

No, zkusme to.

DFS pro binární stromové pole (bez zásobníku a rekurze)

Jako v BFS začínáme od kořenového indexu 0.
Poté musíme zkontrolovat jeho levého potomka, jehož index bychom mohli vypočítat podle vzorce 2*i+1.
Voláme proces přechodu na dalšího levého potomka zdvojením.

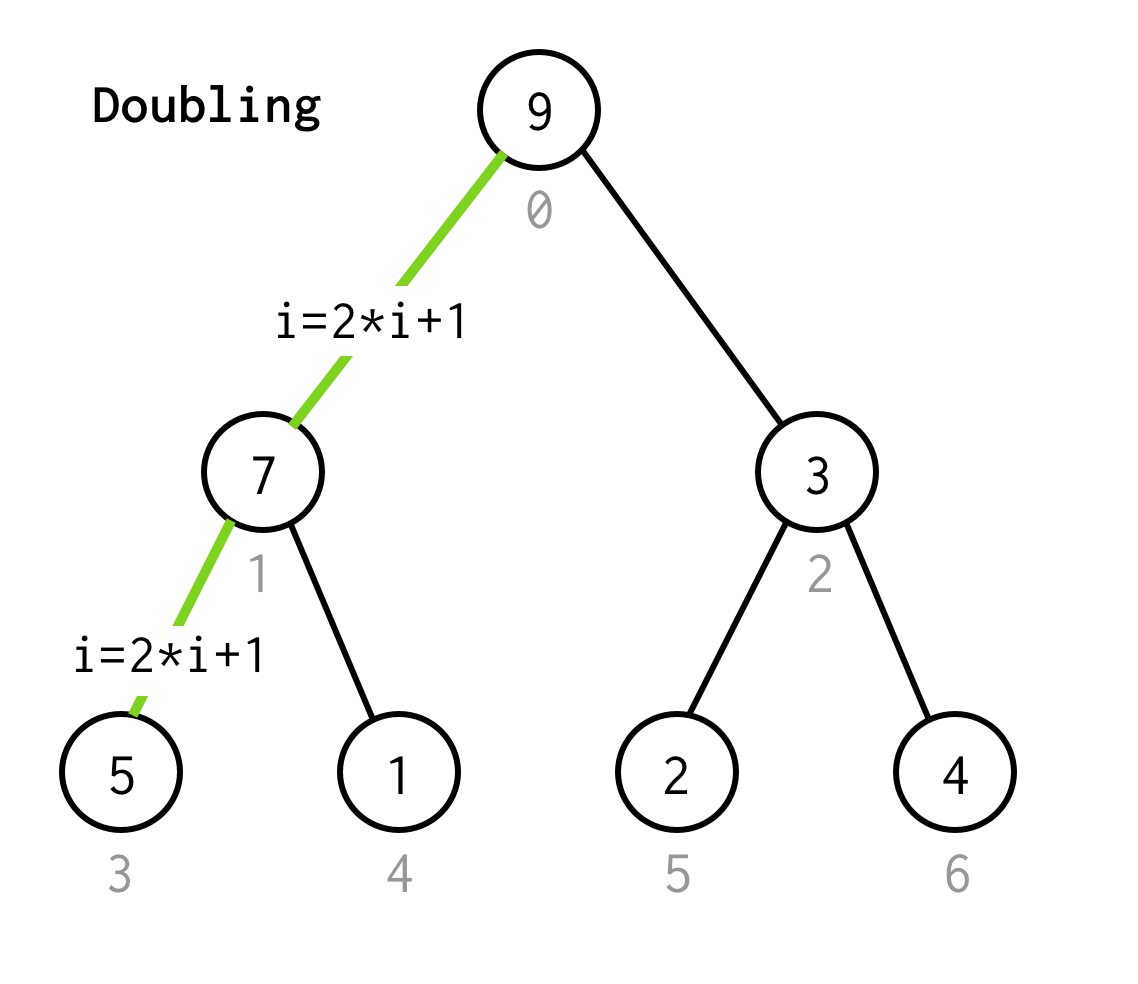
Pokračujeme ve zdvojování indexu, dokud se nezastavíme u listového uzlu.

Jak tedy pochopíme, že se jedná o listový uzel?

Pokud další levý potomek vyprodukuje výjimku indexu mimo hranice pole, musíme přestat zdvojovat a přejít na pravého potomka.

To je správné řešení, ale můžeme se vyhnout zbytečnému zdvojování.

Pozorování zde je, že počet prvků ve stromě nějakého height je dvakrát větší (a plus jeden)než strom s height - 1.

Pro strom s height = 2 máme 7 prvků, pro strom s height = 3 máme 7*2+1 = 15 prvků.

Pomocí tohoto pozorování sestavíme jednoduchou podmínku

i < array.length / 2

Můžeme ověřit, že tato podmínka platí pro libovolný nelistový uzel stromu.

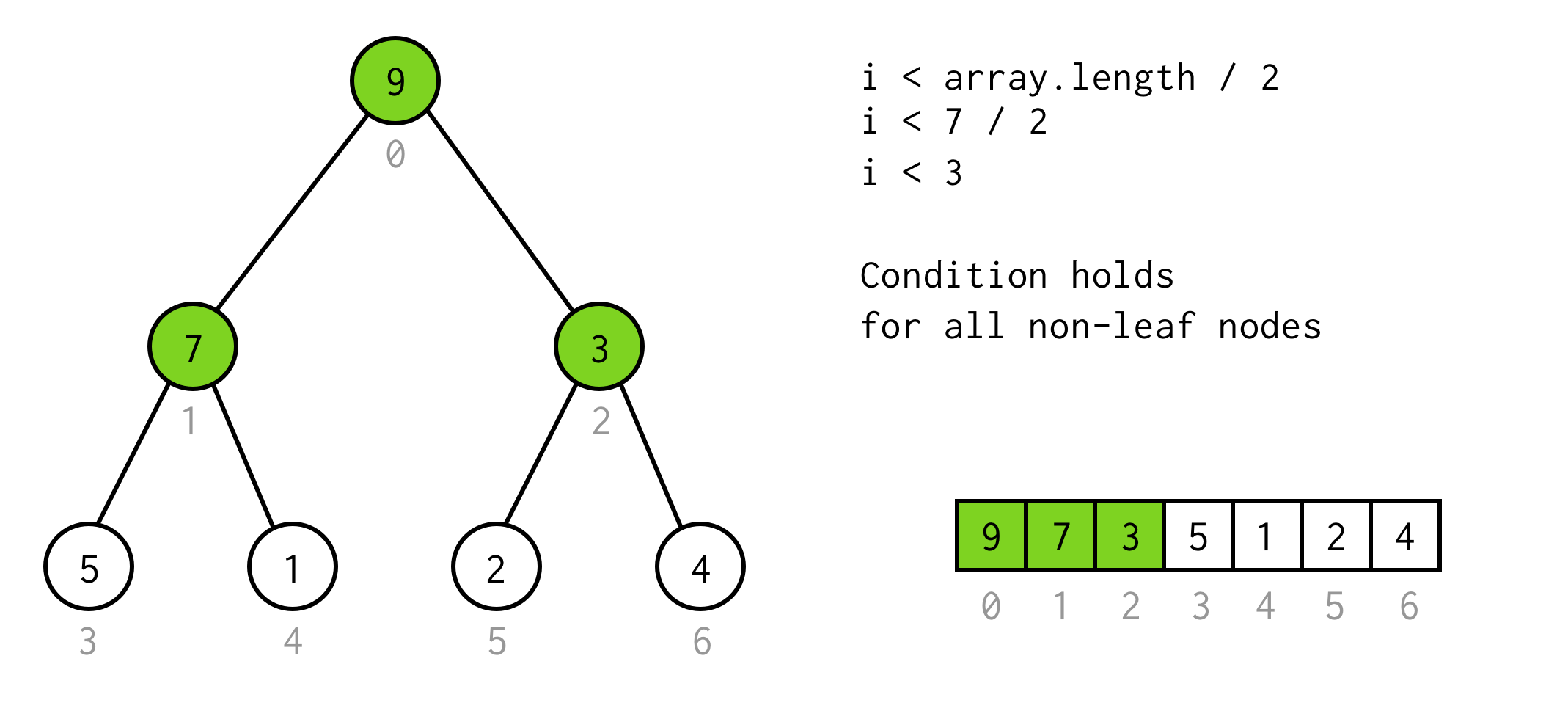
Takže zatím pěkně. Můžeme spustit zdvojení, a dokonce víme, kdy přestat, ale takto můžeme kontrolovat pouze levé potomky uzlů.

Když se zasekneme u listového uzlu a nemůžeme již použít zdvojení, provedeme operaci skoku.V zásadě platí, že pokud zdvojení přejde na levého potomka, skok znamená přejít na rodiče a přejít na pravého potomka.

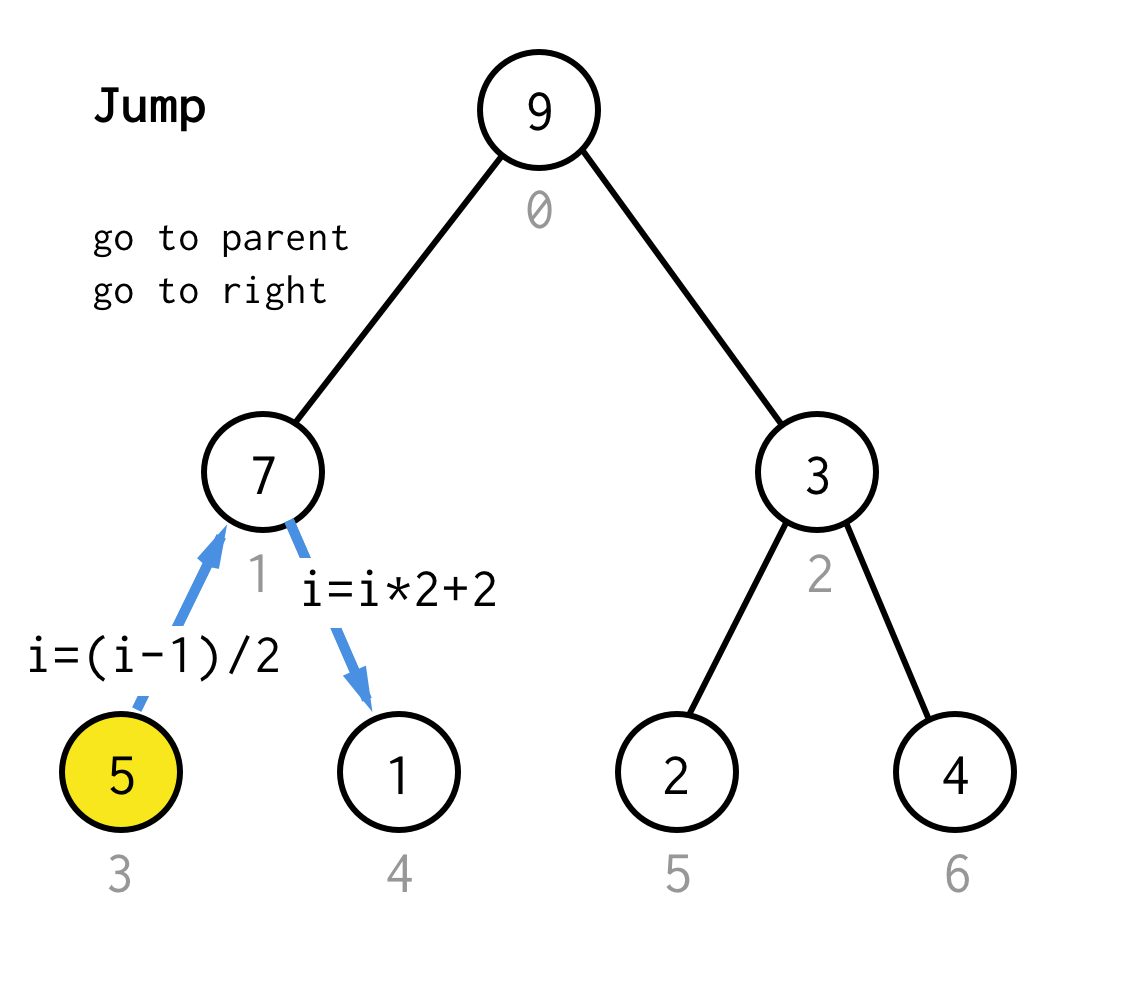
Takovou operaci skoku lze realizovat pouhou inkrementací indexu listu.

Ale když se zasekneme u dalšího listového uzlu, inkrementace neposune uzel na další uzel, což je pro DFS nutné.Proto musíme provést dvojitý skok

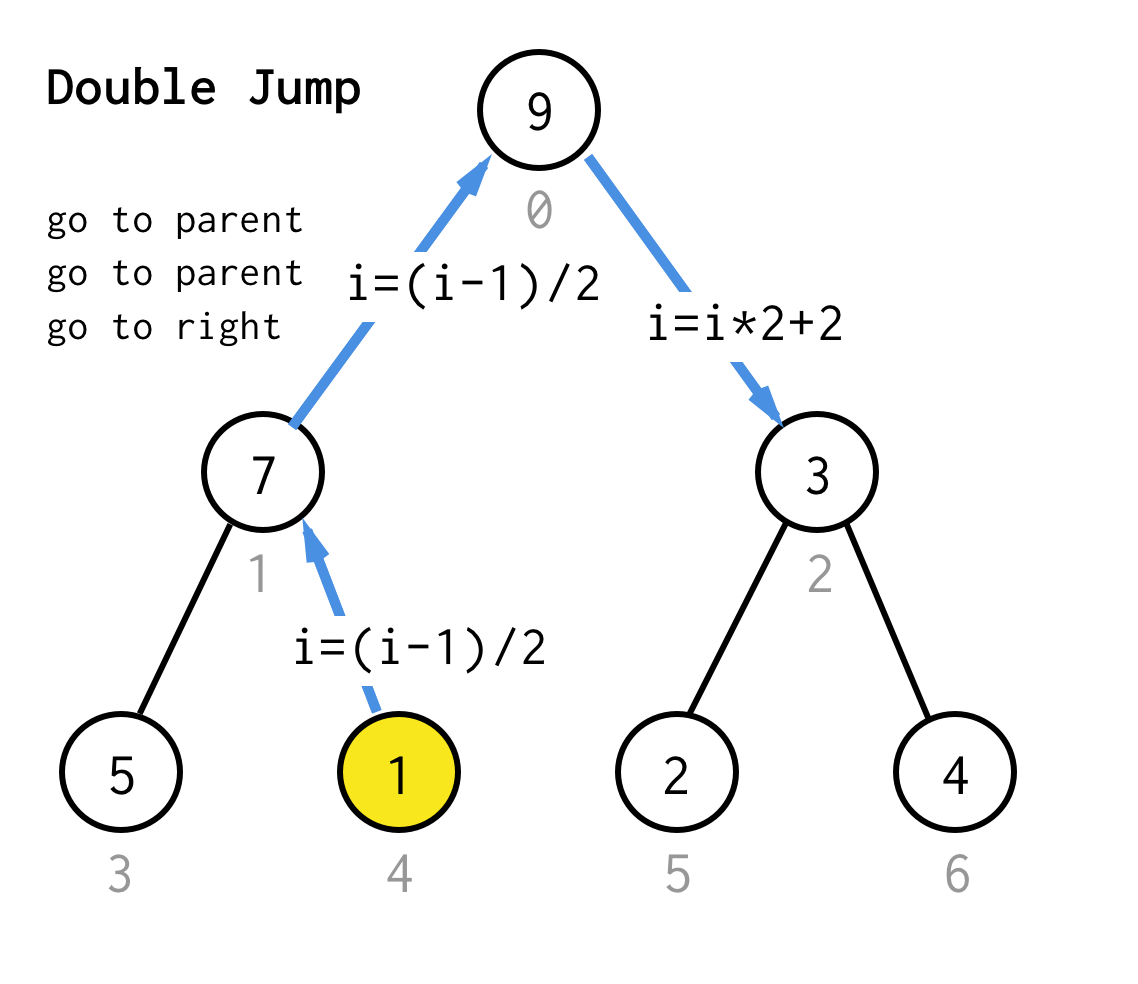
Aby to bylo obecnější, mohli bychom pro náš algoritmus definovat operaci skok N, která určí, kolik skoků k rodiči vyžaduje a vždy skončí jedním skokem k pravému potomkovi.

Pro strom s výškou 1 potřebujeme jeden skok, skok 1

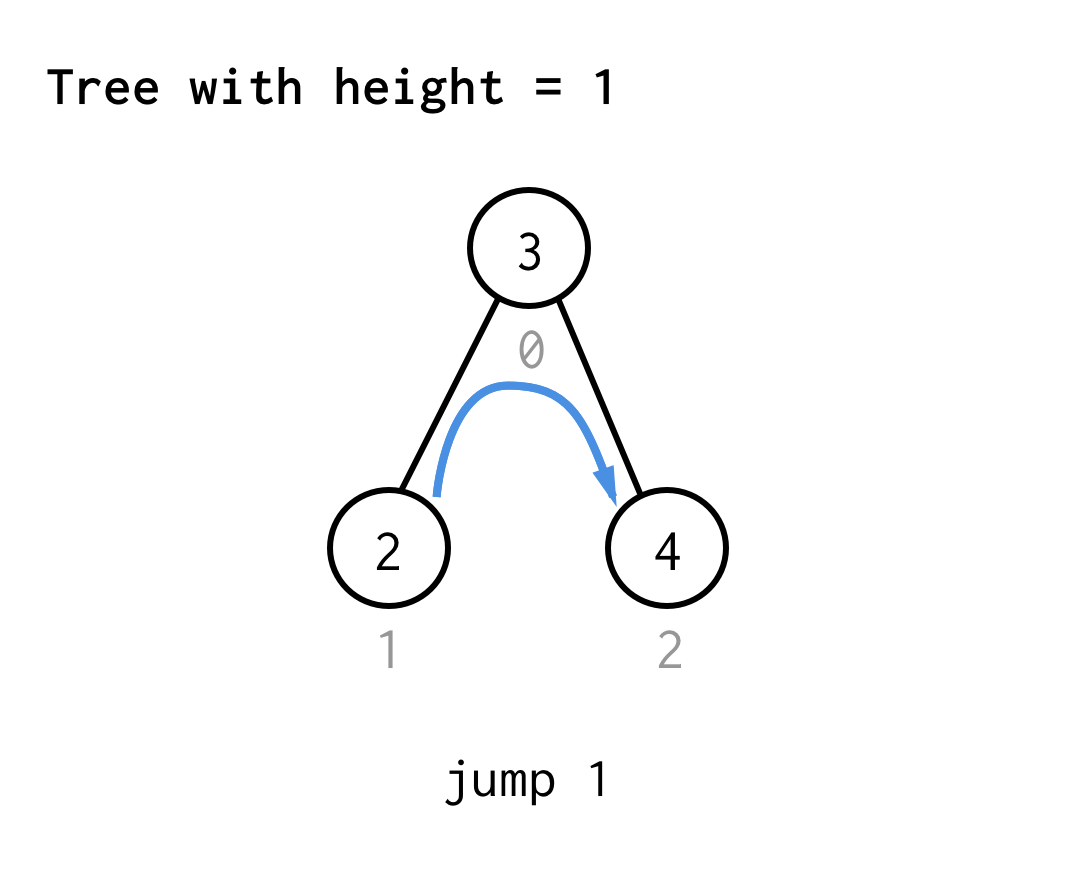
Pro strom s výškou 2 potřebujeme jeden skok, jeden dvojitý skok a než opět jeden skok

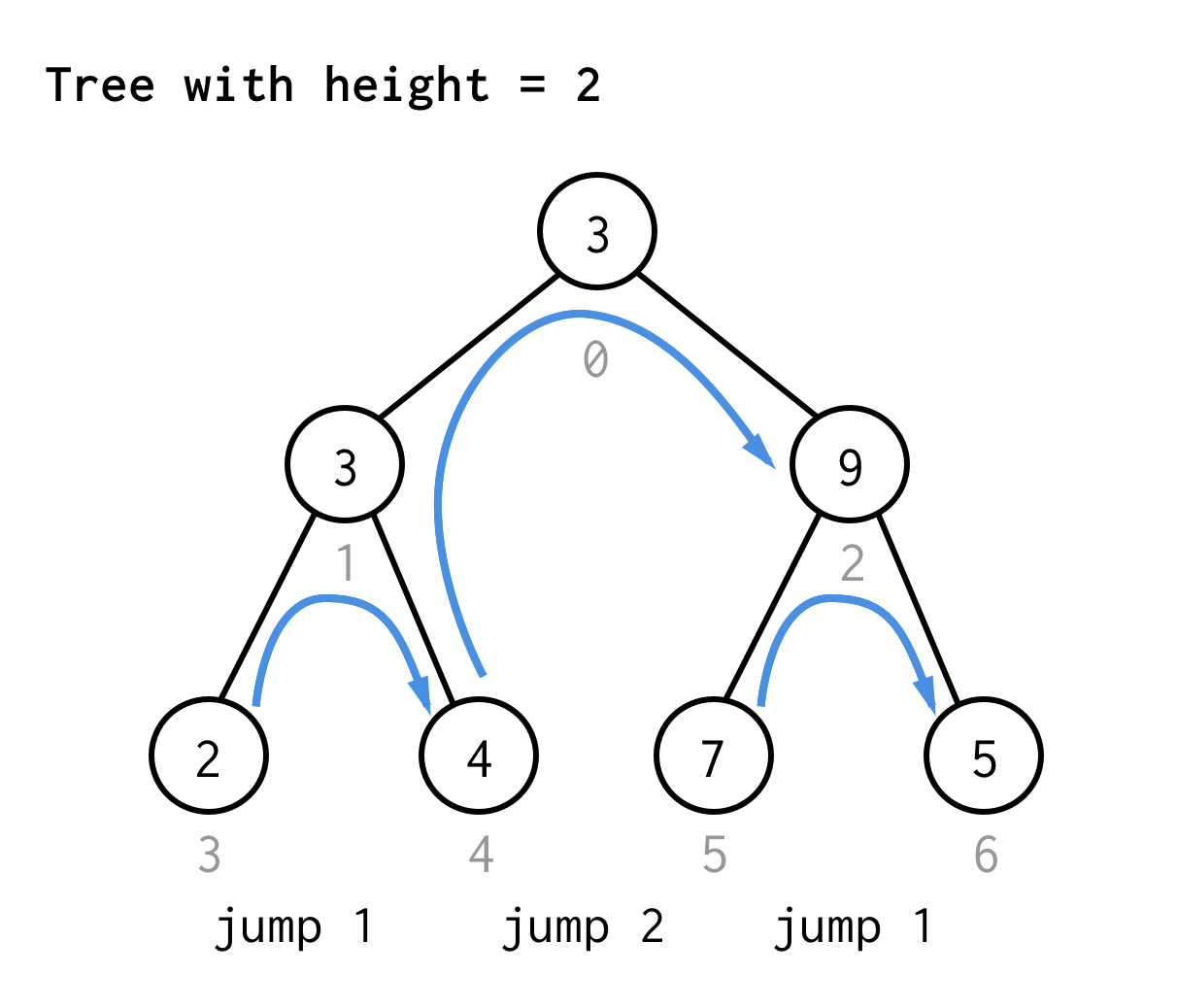
Pro strom s výškou 3 lze použít stejná pravidla a získat 7 skoků.

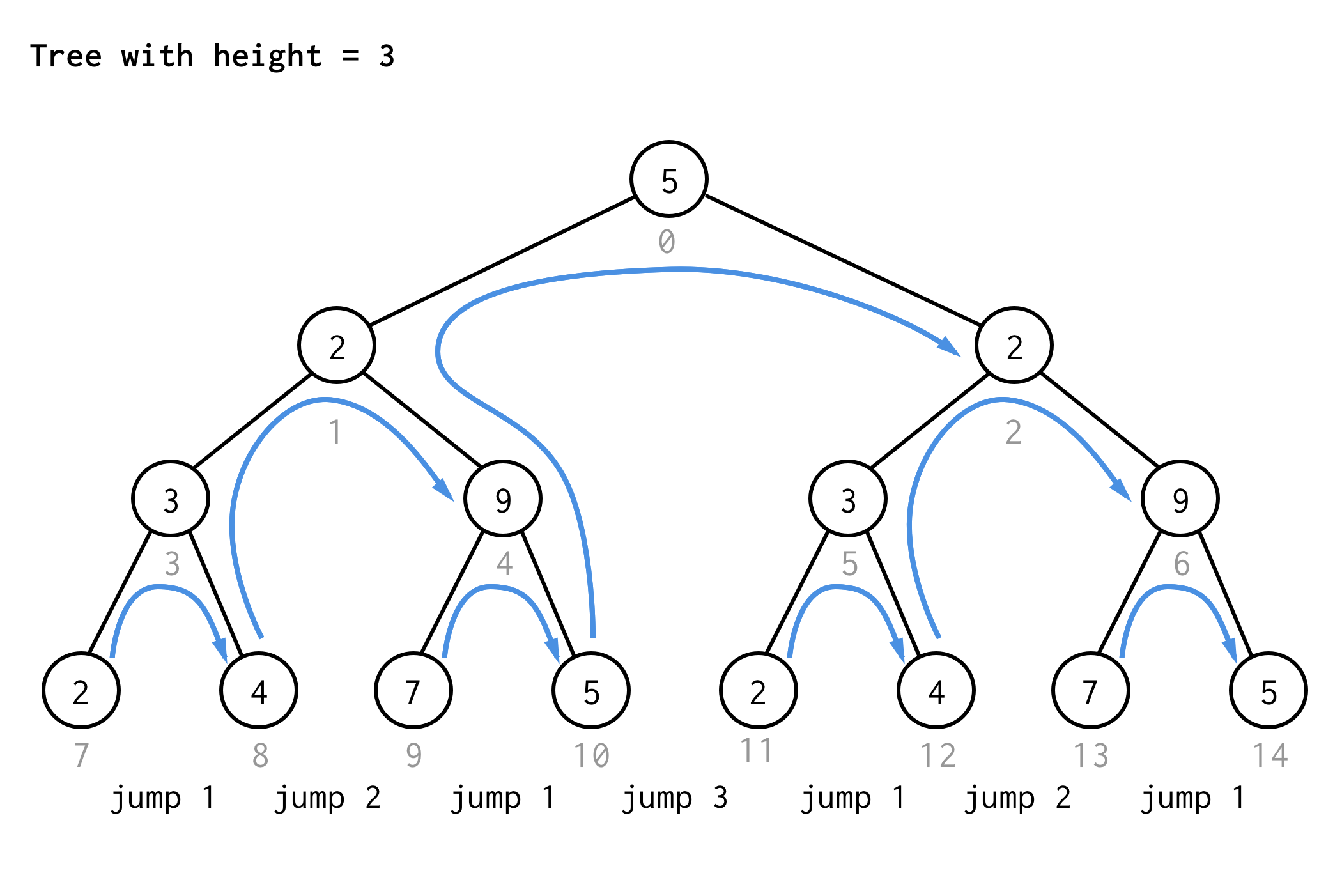
Vidíte ten vzorec?

Pokud aplikujete stejné pravidlo na strom o výšce 4 a zapíšete pouze hodnoty skoků, dostanete další pořadové číslo

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Tuto posloupnost známe jako Ziminova slova a má rekurzivní definici,což není skvělé, protože rekurzi nesmíme používat.

Najdeme nějaký jiný způsob výpočtu.

Pokud se pozorně podíváte na skokovou posloupnost, uvidíte nerekurzivní vzorec.

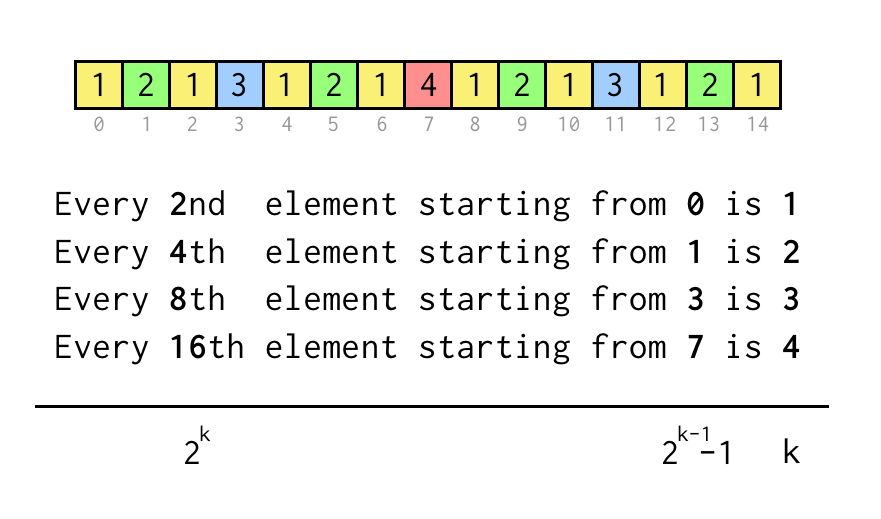
Můžeme sledovat index pro aktuální list j, který odpovídá indexu v poli posloupnosti výše.

Pro ověření příkazu typu „Každý 8. prvek počínaje 3“ stačí zkontrolovat j % 8 == 3,pokud je pravdivý, tři skoky na požadovaný nadřazený uzel.

Iterativní proces skoků bude následující

• Začneme k = 1
• Skočíme jednou na nadřazený uzel použitím i = (i - 1)/2
• Pokud leaf % 2*k == k - 1 všechny skoky provedeme, ukončíme
• V opačném případě nastavíme k na 2*k a opakujeme.

Pokud dáte dohromady vše, co jsme probrali

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Ukončeno. DFS pro binární stromové pole bez zásobníku a rekurze

Složitost

Složitost vypadá jako kvadratická, protože máme smyčku ve smyčce,ale podívejme se, jaká je skutečnost.

• Pro polovinu z celkového počtu uzlů (n/2) použijeme strategii zdvojení, která je konstantní O(1)
• Pro druhou polovinu z celkového počtu uzlů (n/2) použijeme strategii listových skoků.
• Polovina listových skoků (n/4) vyžaduje pouze jeden rodičovský skok, 1 iteraci. O(1)
• Polovina z této poloviny (n/8) vyžaduje dva skoky, tedy 2 iterace. O(1)
• …
• Pouze jeden listový skokový uzel vyžaduje plný skok do kořene, což je O(logN)
• Takže pokud všechny případy mají O(1) kromě jednoho, který je O(logN), můžeme říci, že průměr pro skok je O(1)
• Celková složitost je O(n)

Výkon

Ačkoli teorie je dobrá, podívejme se, jak tento algoritmus funguje v praxi, ve srovnání s ostatními.

Testujeme 5 algoritmů, přičemž používáme JMH.

• BFS na binárním stromu (spojový seznam jako fronta)
• BFS na poli binárního stromu (lineární prohledávání)
• DFS na binárním stromu (zásobník)
• DFS. na binárním stromovém poli (zásobník)
• Iterativní DFS na binárním stromovém poli

Předvytvořili jsme strom a pomocí predikátu hledáme poslední uzel,abychom měli jistotu, že u všech algoritmů narazíme vždy na stejný počet uzlů.

Takže výsledky

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Očividně vyhrává BFS na poli. Je to prostě lineární prohledávání, takže pokud můžete binární strom reprezentovat jako pole, udělejte to.

Iterativní DFS, který jsme právě popsali v článku, obsadil 2druhé místoa 4.5krát pomalejší než lineární prohledávání (BFS na poli)

Zbylé tři algoritmy jsou ještě pomalejší než iterativní DFS, pravděpodobně proto, že zahrnujídalší datové struktury, další prostor a alokaci paměti.

A nejhorší případ je BFS na binárním stromu. Mám podezření, že zde je problémem spojový seznam.

Závěr

Binární stromové pole je pěkný trik, jak reprezentovat hierarchickou datovou strukturujako statické pole (souvislou oblast v paměti). Definuje jednoduchý indexový vztahpro pohyb z rodiče na potomka, stejně jako pro pohyb z potomka na rodiče, což není možnépři klasické reprezentaci binárního pole. Existují určité nevýhody, jako je pomalé vkládání/mazání, ale jsem si jist, že pro binární stromové pole existuje spousta aplikací.

Jak jsme ukázali, vyhledávací algoritmy, BFS a DFS implementované na polích jsou mnohem rychlejší než jejich bratři na referenční struktuře. Pro reálné problémy to není tak důležité a pravděpodobně budu stále používat binární pole založené na referencích.

V každém případě to bylo pěkné cvičení. Na příštím pohovoru očekávejte otázku „DFS na binárním poli bez rekurze a zásobníku“.

• algoritmy
• datové struktury
• programování

mishadoff 10. září 2017