Privacitet & Cookies
Denna webbplats använder cookies. Genom att fortsätta godkänner du att de används. Läs mer, bland annat om hur du kontrollerar cookies.
En spiral är en kurva som ”utgår från en punkt och som rör sig längre bort när den kretsar runt punkten”.

Det finns många olika typer av spiraler, beroende på de formler som skapar dem. I det här blogginlägget kommer jag att diskutera tvådimensionella spiraler (observera att det även finns en mängd tredimensionella spiraler).
Arkimedisk spiral
Detta är en spiral som är uppkallad efter den berömde grekiske matematikern Arkimedes, som var den förste att beskriva den i sin bok On Spirals. Den beskrivs av följande polära ekvation:
där a och b är reella tal.
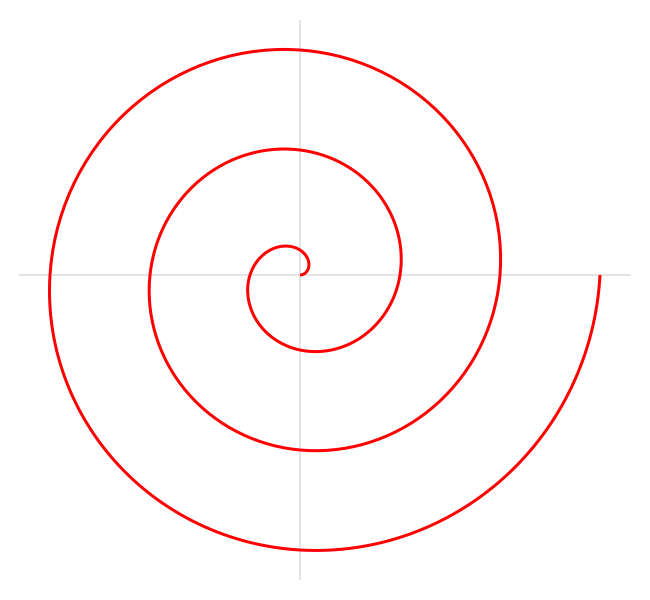
Då man ändrar parametern a kommer spiralen att vrida sig och parametern b kontrollerar avståndet mellan på varandra följande vändningar.
Fermats spiral
Fermats spiral är en parabolisk spiral som lyder följande polära ekvation:
Det är en typ av arkimedisk spiral.

Eulers spiral
Också känd som Cornu-spiral är det en kurva vars krökning ökar när avståndet från ursprunget ökar; ”krökningen av en cirkulär kurva är lika med reciproken av radien”.

Parameterformen består av två ekvationer med Fresnels intervall, som endast kan lösas ungefärligt.
Dessa integraler, och därmed Eulers spiral, kan användas för att beskriva energifördelningen av Fresnels diffraktion vid en enda spalt i vågteori.
Hyperbolisk spiral
Den hyperboliska spiralen, som först uppfattades av Pierre Varignon 1704, är en transcendentalkurva, vilket innebär att ”det är en analytisk funktion som inte uppfyller en polynomekvation”. Den är motsatsen till en arkimedisk spiral och har därför följande polära ekvation:
I centrum befinner den sig på ett oändligt avstånd från polen; för θ som börjar vid 0 börjar r vid oändligheten.
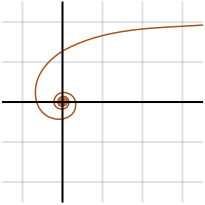
Lituus
Lituus är en spiral med en polär ekvation:
där k är en konstant. Vinkeln är alltså omvänt proportionell mot kvadraten på radien. 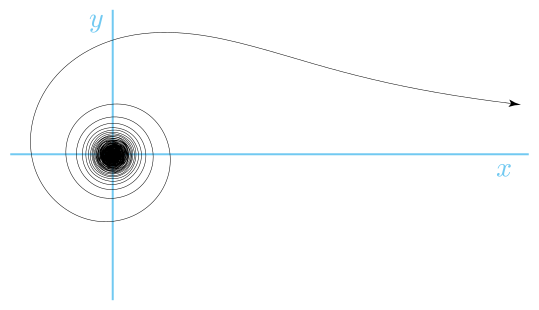
Kurvan fick sitt namn efter den antika romerska lituus (en böjd augurstav eller krigstrumpet) av Roger Cotes i en samling uppsatser som publicerades 1722.
Logaritmisk spiral
 Den logaritmiska spiralen är en självliknande spiral som ofta förekommer i naturen. Den beskrevs först av Descartes, men studerades ingående av Jacob Bernoulli som kallade den ”den underbara spiralen”. Den har en polär ekvation på
Den logaritmiska spiralen är en självliknande spiral som ofta förekommer i naturen. Den beskrevs först av Descartes, men studerades ingående av Jacob Bernoulli som kallade den ”den underbara spiralen”. Den har en polär ekvation på
.





Lämna ett svar