Djupgående första sökning för binärt träd utan stapel och rekursion.
Binary Tree Array
Det här är ett binärt träd.
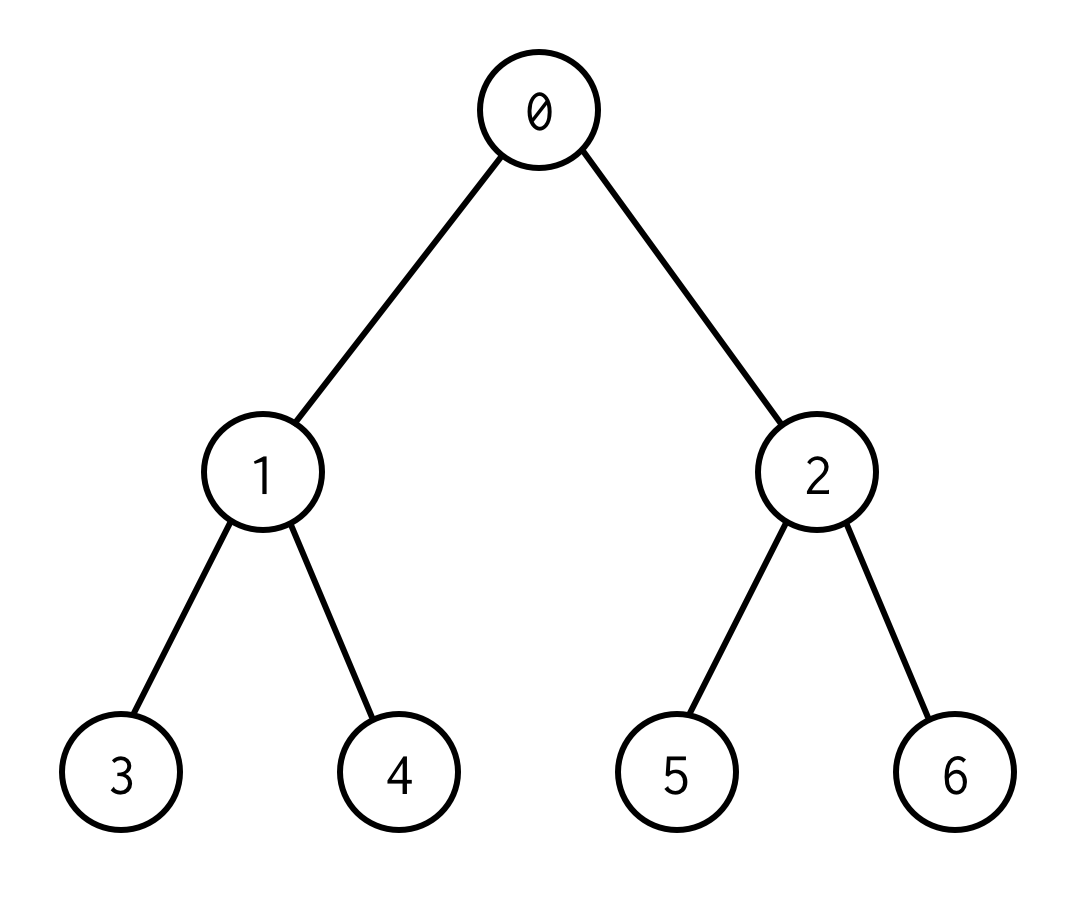
0 är en rotnod.0 har två barn: vänster 1 och höger: 2.
Varje barn har sina barn och så vidare.
Noderna utan barn är bladnoder (3,4,5,6).
Antalet kanter mellan rot- och bladnoder definierar trädets höjd.Trädet ovan har höjden 2.
Standardmetoden för att implementera binära träd är att definiera en klass som heter BinaryNode
public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}Det finns dock ett knep för att implementera binära träd genom att endast använda statiska matriser.Om du räknar upp alla noder i det binära trädet med nivåer som börjar från noll kan du packa in det i en matris.
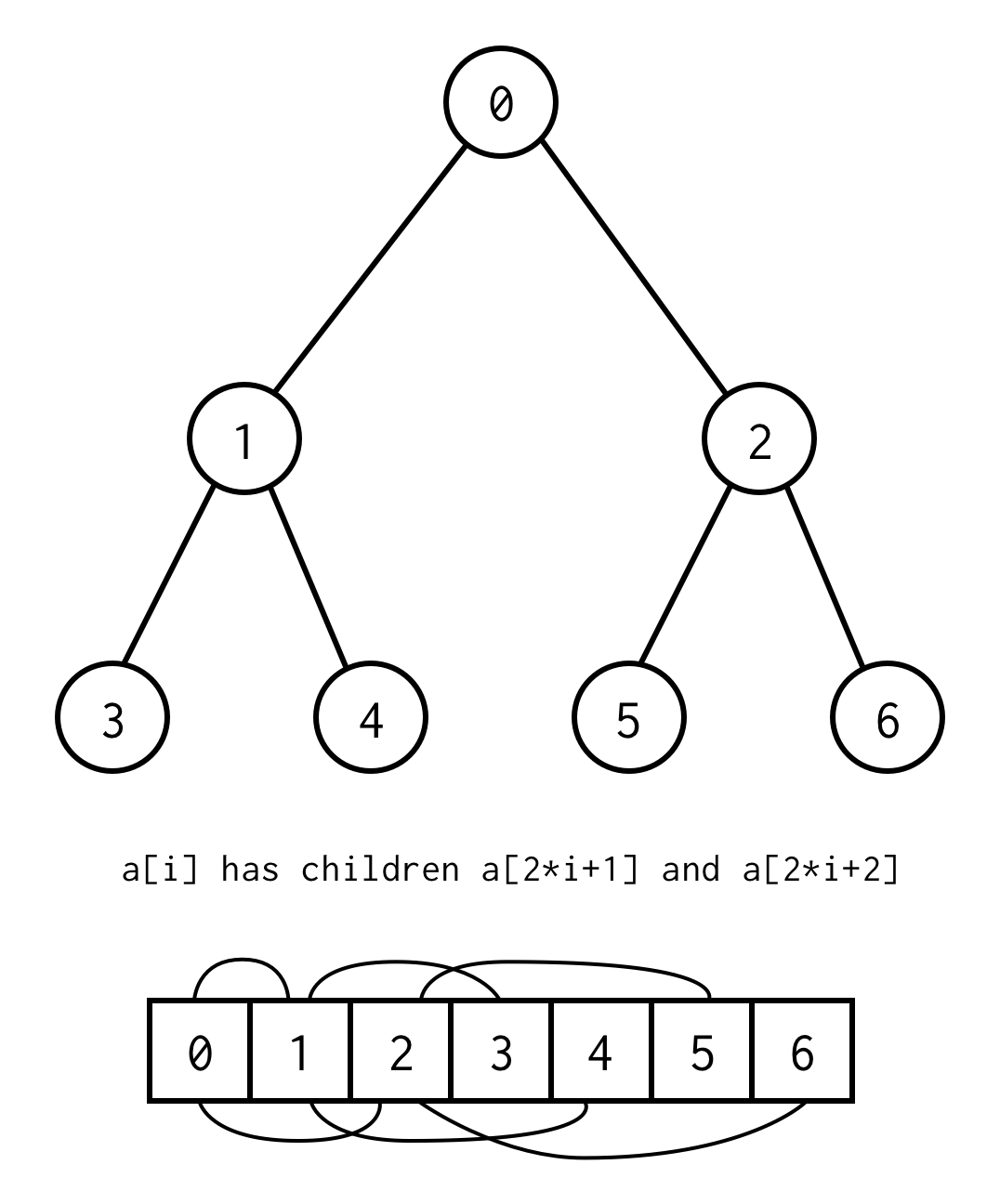
Relationen mellan föräldraindex och barnindex,gör det möjligt för oss att flytta från förälder till barn, samt från barn till förälder
left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2Viktigt att notera att trädet ska vara komplett, vilket innebär att det för den specifika höjden ska innehålla exakt element.
Du kan undvika detta krav genom att placera null i stället för saknade element.Uppräkningen gäller fortfarande för tomma noder också. Detta bör täcka alla möjliga binära träd.
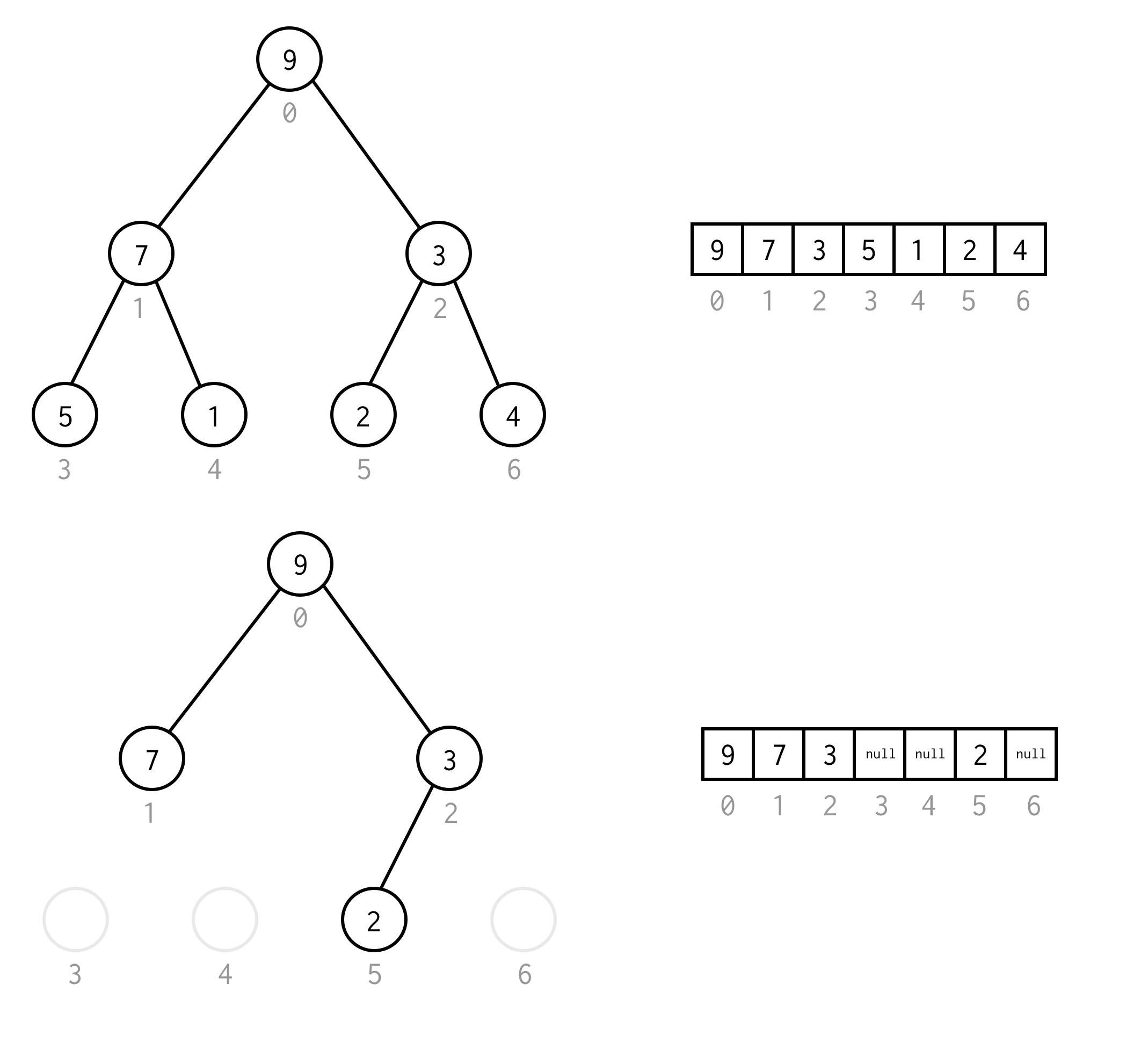
En sådan arrayrepresentation för binära träd kommer vi att kalla Binary Tree Array.Vi antar alltid att den kommer att innehålla element.
BFS vs DFS
Det finns två sökalgoritmer för binära träd: breadth-first search (BFS) och depth-first search (DFS).
Det bästa sättet att förstå dem är visuellt
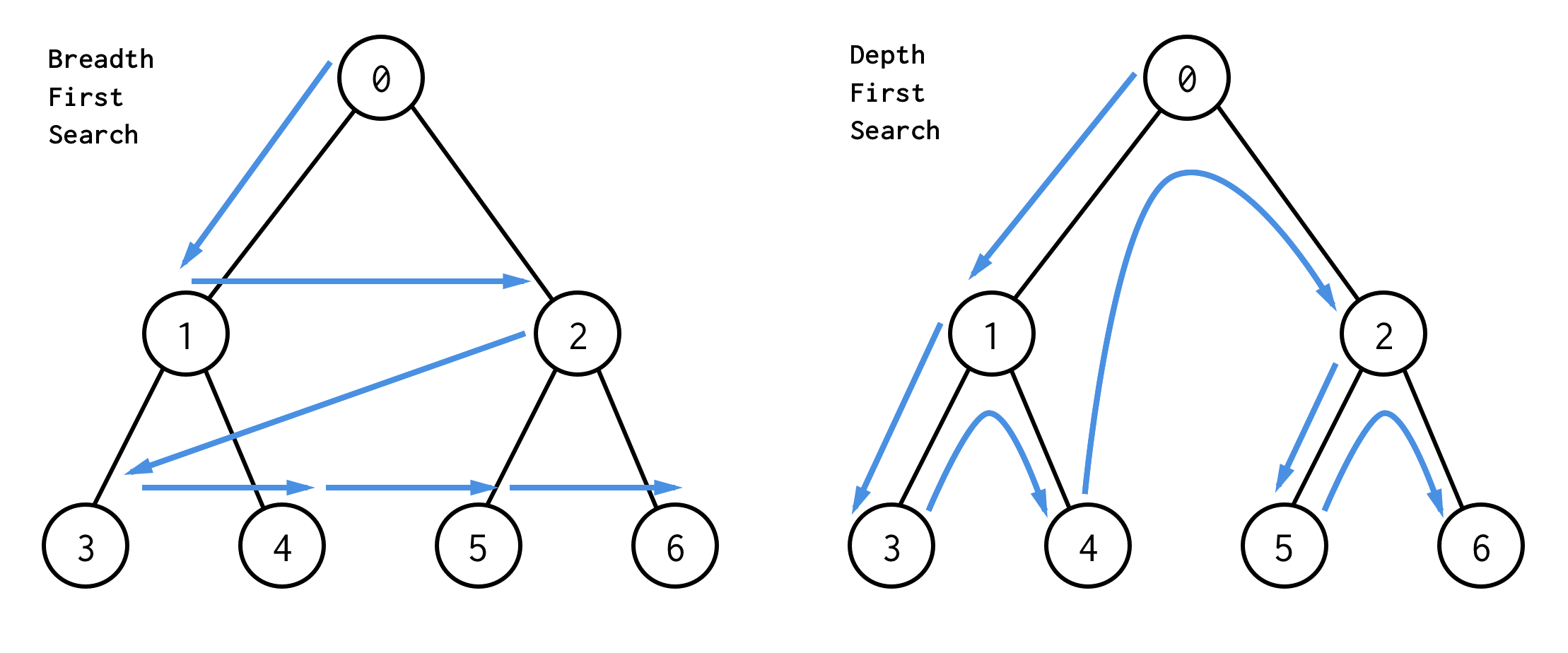
BFS söker i noder nivå för nivå, med utgångspunkt från rotnoden. Därefter kontrolleras dess barn. Sedan barn för barn och så vidare tills alla noder har behandlats eller tills en nod som uppfyller sökvillkoren har hittats.
DFS beter sig på ett annat sätt. Den kontrollerar alla noder från den vänstra vägen från roten till bladet, hoppar sedan upp och kontrollerar den högra noden och så vidare.
För klassiska binära träd implementeras BFS med hjälp av datastrukturen Queue (LinkedList implementerar Queue)
public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}Om man ersätter queue med stack får man DFS-implementering.
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}För att ta ett exempel, anta att du behöver hitta en nod med värdet 1 i följande träd.
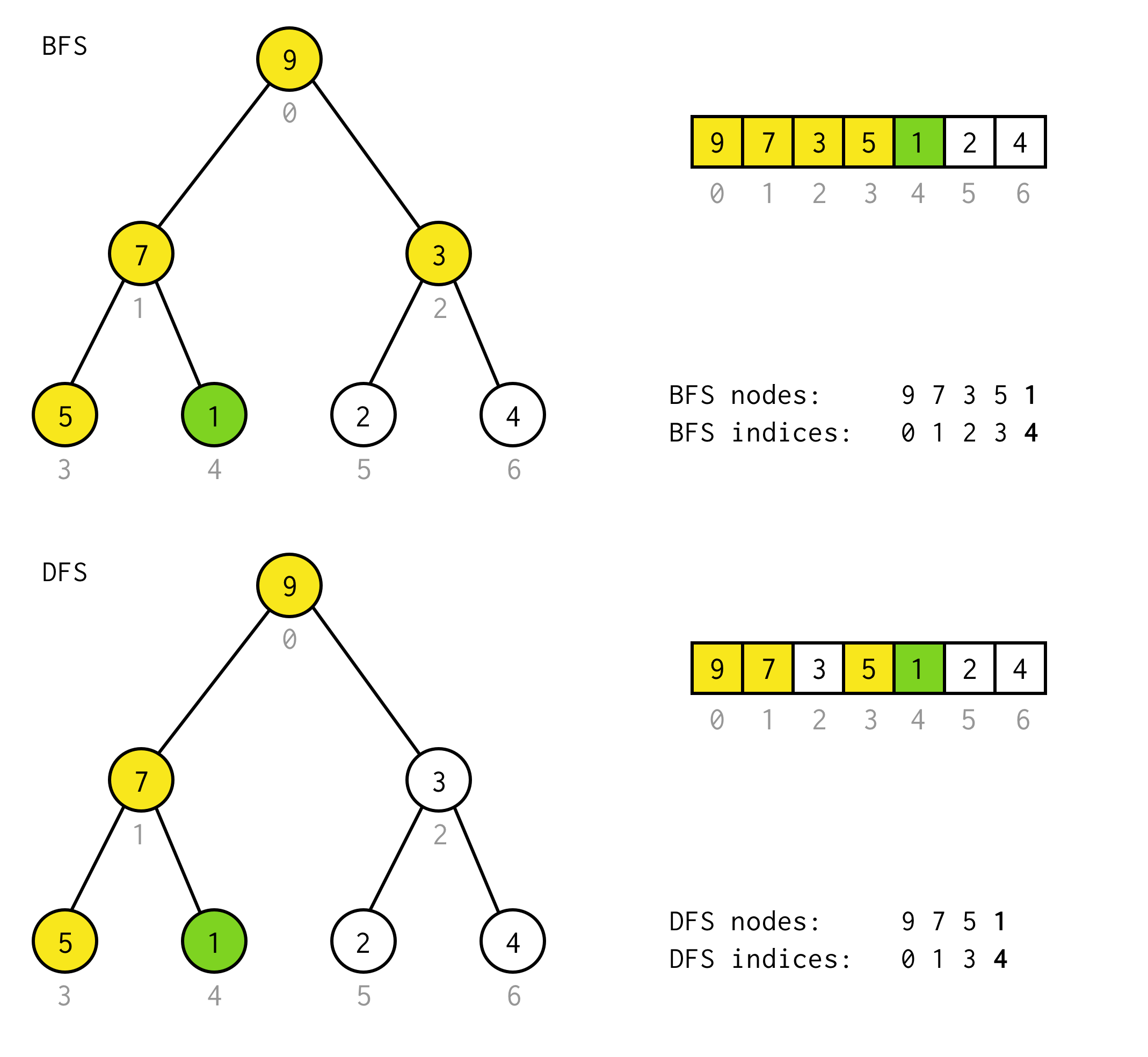
Gula celler är celler som testas i sökalgoritmen innan den behövliga noden hittas.Ta hänsyn till att DFS i vissa fall kräver färre noder för bearbetning.I vissa fall krävs det fler.
BFS och DFS för binära trädmatriser
Bredth-first search för binära trädmatriser är trivialt.Eftersom elementen i binära trädmatriser är placerade nivå för nivå ochbfs också kontrollerar element nivå för nivå är bfs för binära trädmatriser bara linjär sökning
public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}Depth-first search är lite svårare.
Med hjälp av datastrukturen stack kan det implementeras på samma sätt som för klassiska binära träd, det är bara att sätta index i stapeln.
Från den här punkten skiljer sig rekursion inte alls, man använder bara implicit metodanropstack i stället för datastrukturen stack.
Tänk om vi kunde implementera DFS utan stack och rekursion.I slutändan är det bara att välja rätt index i varje steg?
Ja, låt oss försöka.
DFS for Binary Tree Array (without stack and recursion)
Som i BFS börjar vi från rotindex 0.
Därefter måste vi inspektera dess vänstra barn, vars index kan beräknas med formel 2*i+1.
Låt oss kalla processen att gå till nästa vänstra barn för fördubbling.
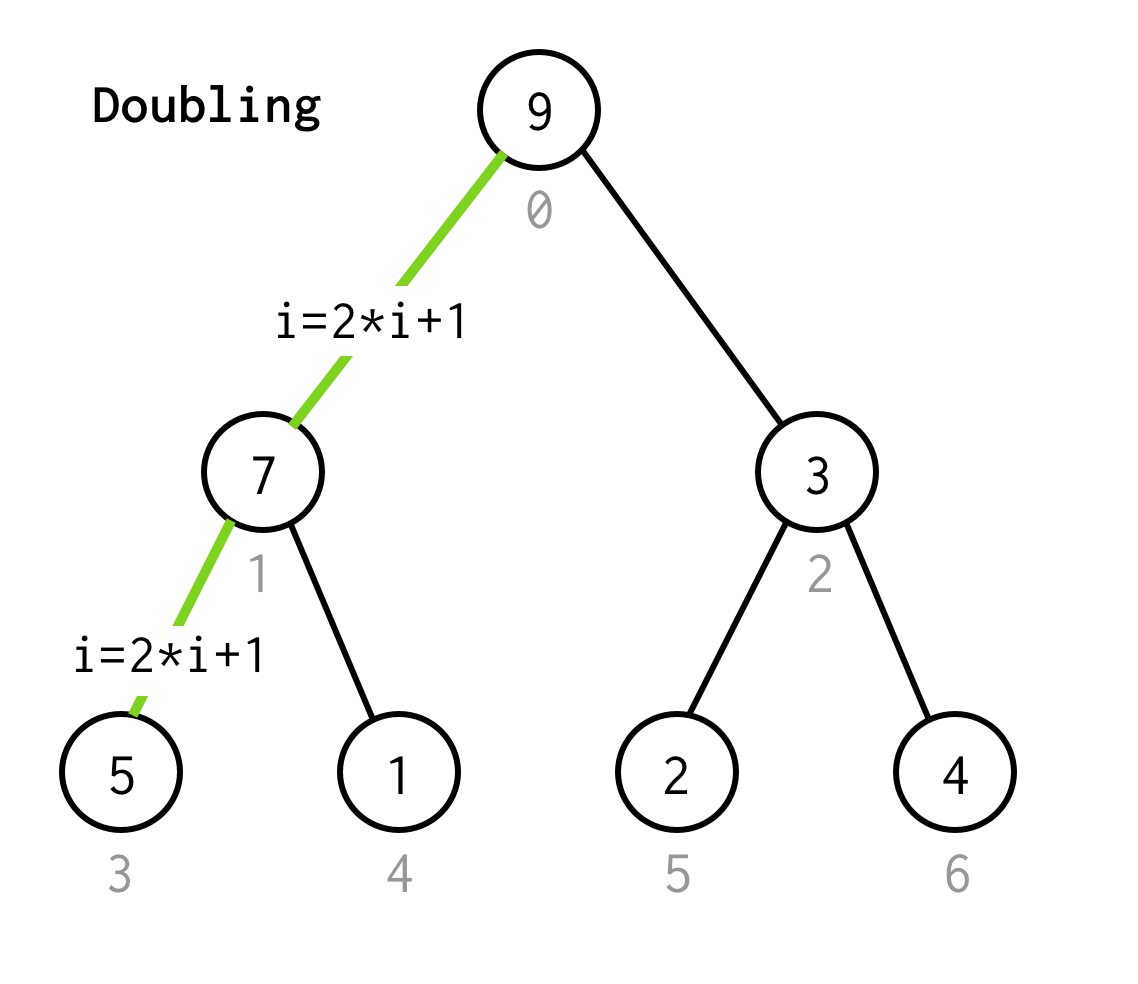
Vi fortsätter att fördubbla indexet tills vi inte stannar vid bladnoden.
Hur kan vi då förstå att det är en bladnod?
Om nästa vänstra barn ger index utanför arrayens gränser måste vi sluta fördubbla och hoppa till det högra barnet.
Det är en giltig lösning, men vi kan undvika onödig fördubbling.Observationen här är att antalet element i trädet med vissa height är två gånger större (och plus en)än trädet med height - 1.
För träd med height = 2 har vi 7 element, för träd med height = 3 har vi 7*2+1 = 15 element.
Med hjälp av denna observation bygger vi upp ett enkelt villkor
i < array.length / 2Det går att kontrollera att detta villkor är giltigt för alla icke-bladiga noder i trädet.
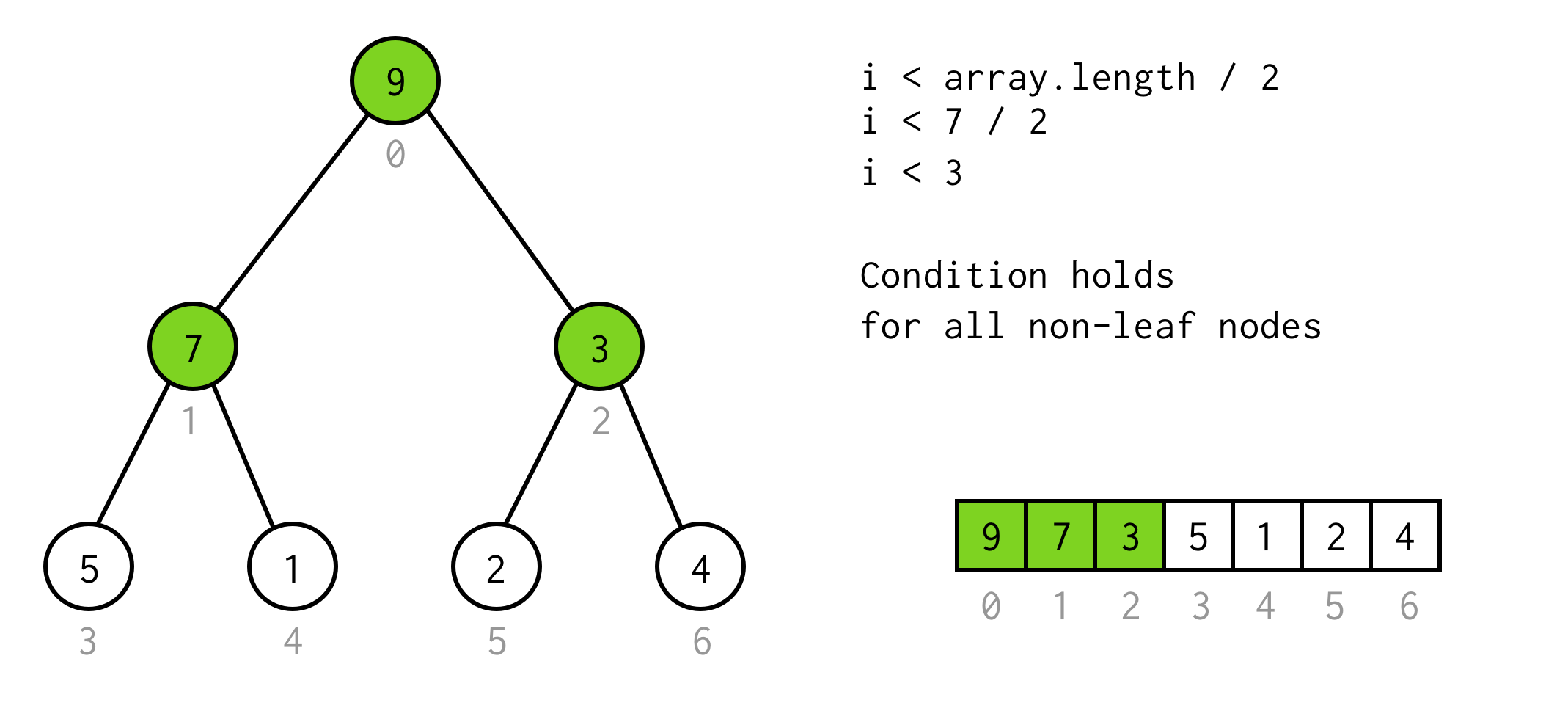
Snyggt så här långt. Vi kan köra fördubbling och vi vet till och med när vi ska sluta, men på det här sättet kan vi bara kontrollera nodernas vänstra barn.
När vi fastnat vid en bladnod och inte kan tillämpa fördubbling längre, utför vi en hoppoperation.Om fördubbling är att gå till vänster barn, är hopp att gå till förälder och gå till höger barn.
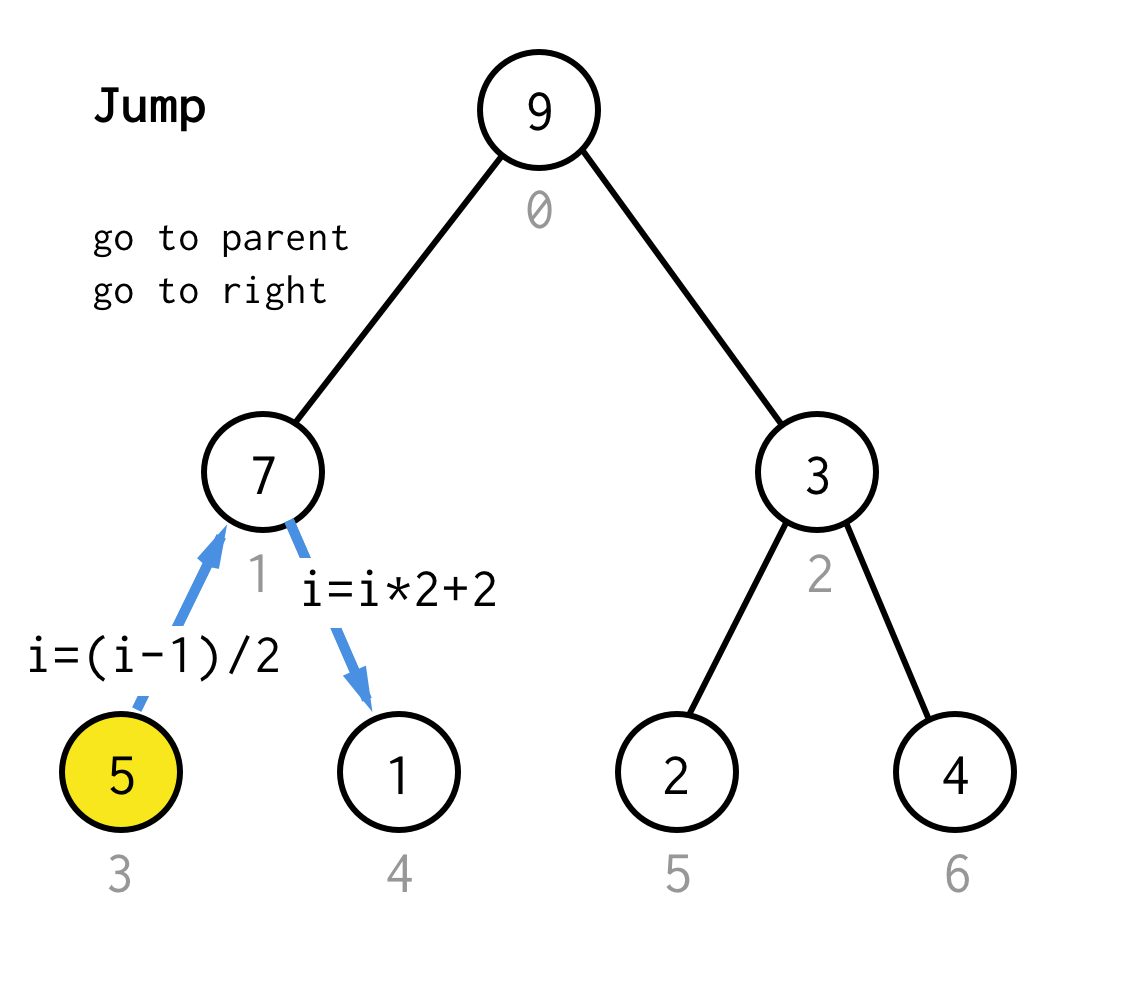
Den här typen av hoppoperation kan genomföras genom att bara öka bladindexet, men när vi fastnat vid nästa bladnod flyttar inte ökningen noden till nästa nod, vilket krävs för DFS.Så vi måste göra dubbla hopp
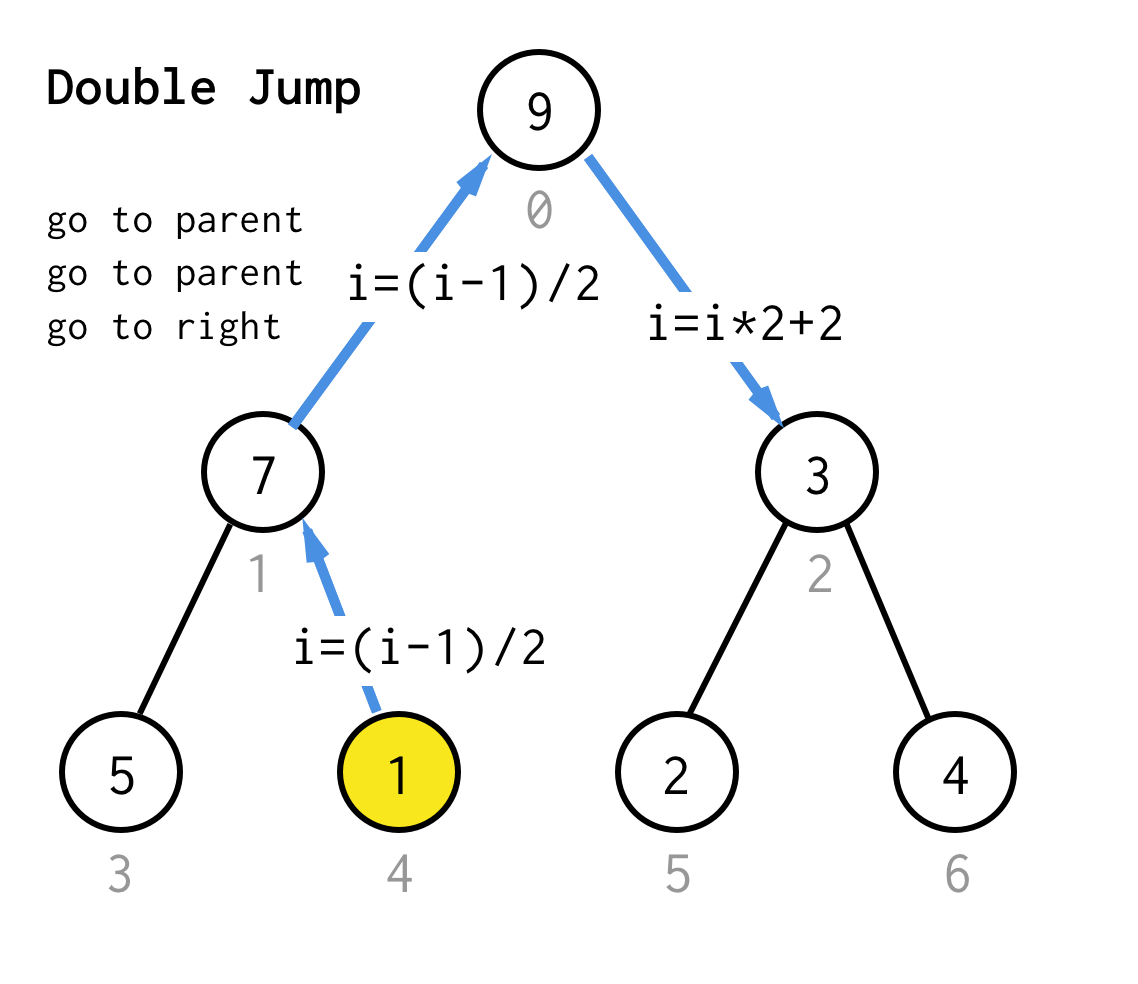
För att göra det mer generiskt kan vi för vår algoritm definiera operationen jump N, som anger hur många hopp till föräldern som krävs och som alltid avslutas med ett hopp till rätt barn.
För trädet med höjd 1 behöver vi ett hopp, hopp 1
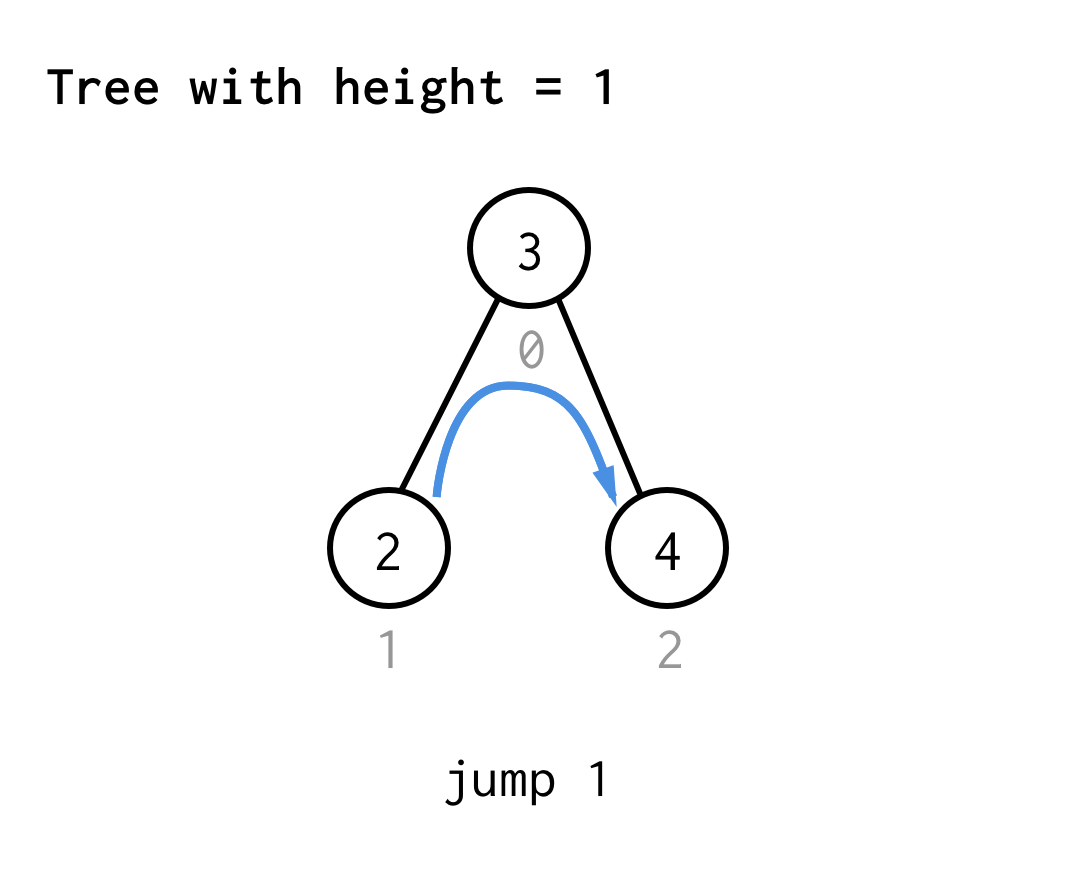
För trädet med höjd 2 behöver vi ett hopp, ett dubbelhopp och sedan ett hopp igen
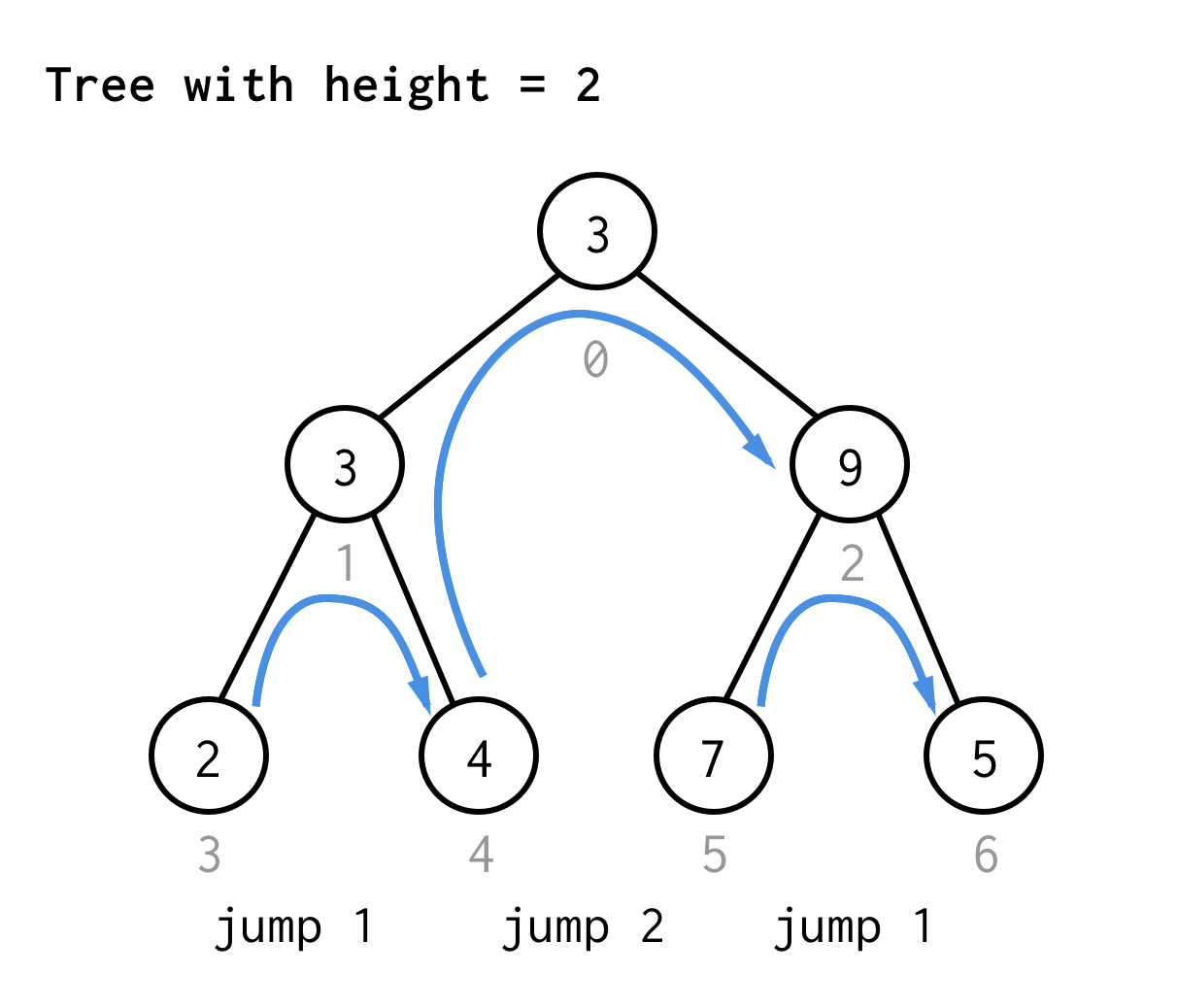
För trädet med höjd 3 kan man tillämpa samma regler och få 7 hopp.
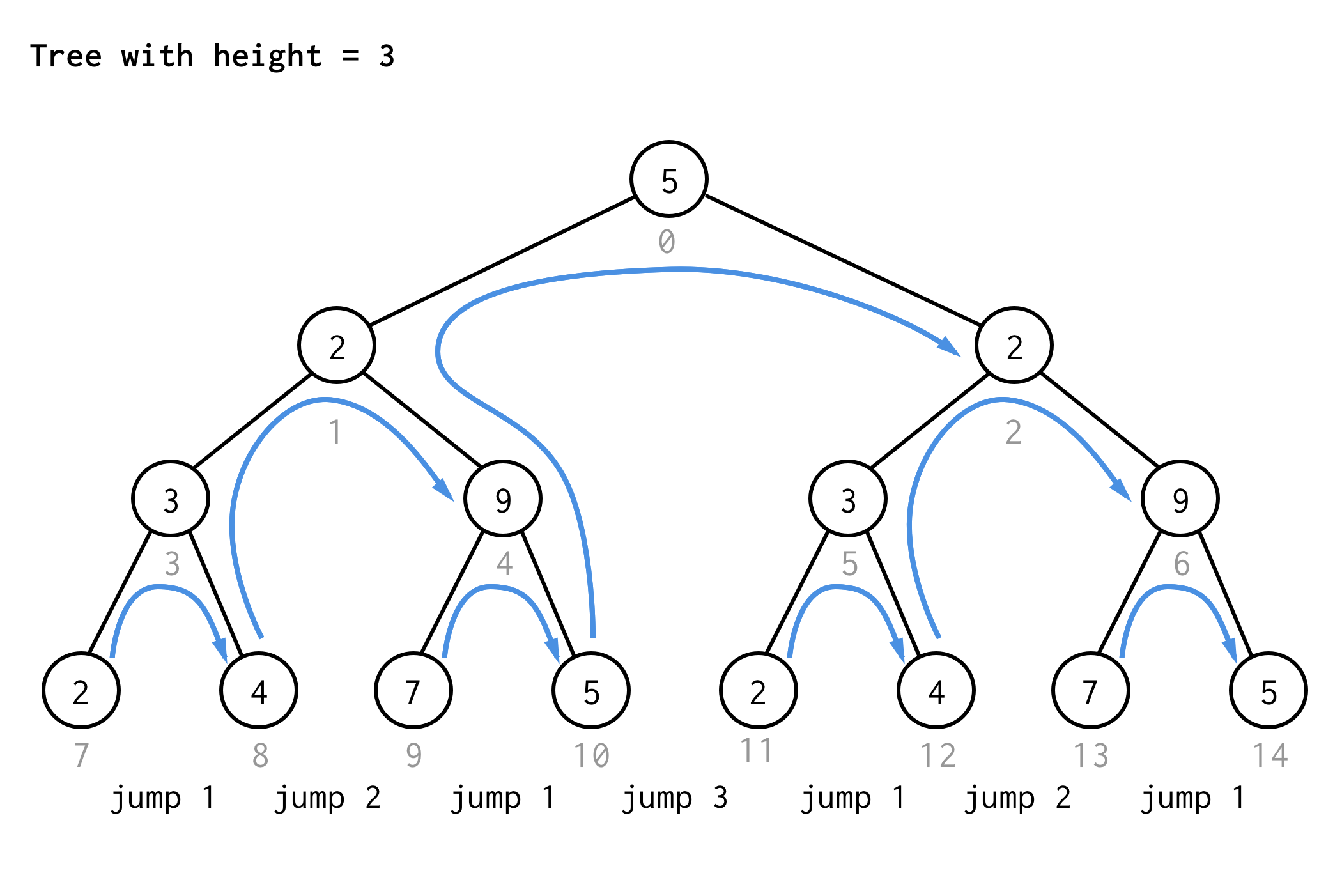
Se mönstret?
Om du tillämpar samma regel på trädet med höjd 4 och skriver ner endast hoppvärden får du nästa sekvensnummer
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
Denna sekvens är känd som Zimin-ord och den har en rekursiv definition, vilket inte är så bra, eftersom vi inte får använda rekursion.
Låt oss hitta ett annat sätt att beräkna det.
Om du tittar noga på hoppsekvensen kan du se ett icke-rekursivt mönster.
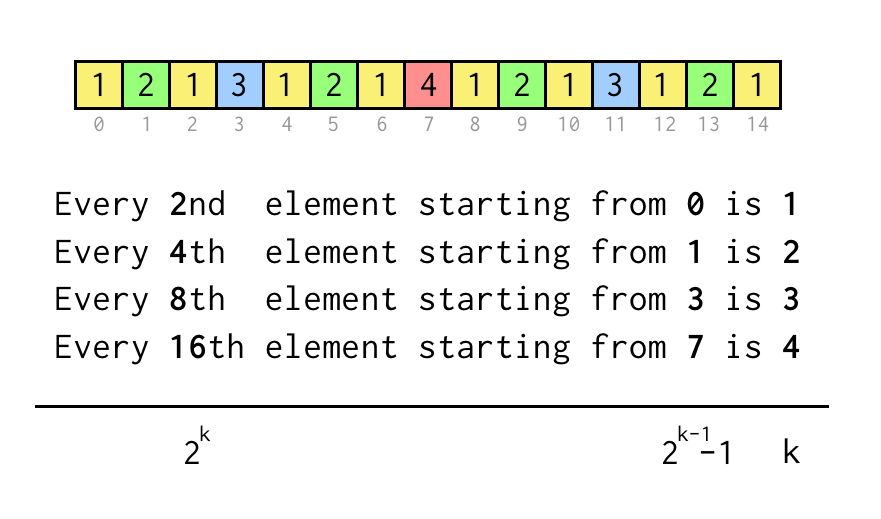
Vi kan spåra index för aktuellt blad j, vilket motsvarar indexet i sekvensmatrisen ovan.
För att verifiera ett påstående som ”Varje åttonde element börjar från 3” kontrollerar vi bara j % 8 == 3, om det är sant krävs tre hopp till den överordnade noden.
Iterativ hoppprocess blir följande
- Start med
k = 1 - Springa en gång till den överordnade noden genom att tillämpa
i = (i - 1)/2 - Om
leaf % 2*k == k - 1alla hopp är utförda, avsluta - I annat fall, sätt
ktill2*koch upprepa.
Om du sätter ihop allt det vi har diskuterat
public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}Gjort. DFS för binär trädmatris utan stack och rekursion
Komplexitet
Komplexiteten ser ut att vara kvadratisk eftersom vi har en slinga i en slinga, men låt oss se hur verkligheten ser ut.
- För hälften av de totala noderna (
n/2) använder vi dubbleringsstrategi, som är konstantO(1) - För den andra hälften av de totala noderna (
n/2) använder vi bladhoppningsstrategi. - Hälften av de bladhoppande noderna (
n/4) kräver endast ett föräldrahopp, 1 iteration.O(1) - Hälften av denna halva (
n/8) kräver två hopp, eller 2 iterationer.O(1) - …
- Endast en bladhoppande nod kräver fullt hopp till roten, vilket är
O(logN) - Så, om alla fall har
O(1)utom ett som ärO(logN), kan vi säga att genomsnittet för hopp ärO(1) - Total komplexitet är
O(n)
Prestanda
Tyvärr är teorin bra, men låt oss se hur denna algoritm fungerar i praktiken och jämföra med andra.
Vi testar fem algoritmer med hjälp av JMH.
- BFS på binärt träd (länkad lista som kö)
- BFS på binärt träd array (linjär sökning)
- DFS på binärt träd (stack)
- DFS on Binary Tree Array (stack)
- Iterativ DFS on Binary Tree Array
Vi har skapat ett träd i förväg och använder predikat för att matcha den sista noden,för att se till att vi alltid träffar samma antal noder för alla algoritmer.
Så, resultat
Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/sOppenbart vinner BFS på array. Det är bara en linjär sökning, så om du kan representera binärt träd som array, gör det.
Iterativ DFS, som vi just beskrev i artikeln, tog 2den andra platsen och var 4.5 gånger långsammare än linjär sökning (BFS på array)
Resten av de tre algoritmerna är till och med långsammare än iterativ DFS, troligen för att de involverar ytterligare datastrukturer, extra utrymme och minnesallokering.
Och i det värsta fallet är BFS på binärt träd. Jag misstänker att den länkade listan är ett problem här.
Slutsats
Binary Tree Array är ett bra knep för att representera hierarkiska datastrukturer som en statisk array (sammanhängande område i minnet). Den definierar ett enkelt indexförhållande för att flytta från förälder till barn och från barn till förälder, vilket inte är möjligt med klassisk binär matrisrepresentation. Det finns vissa nackdelar, t.ex. långsam insättning/släckning, men jag är säker på att det finns många tillämpningar för binära trädmatriser.
Som vi har visat är sökalgoritmer, BFS och DFS som implementeras på matriser mycket snabbare än deras bröder på en referensbaserad struktur. För verkliga problem är det inte så viktigt, och förmodligen kommer jag fortfarande att använda den referensbaserade binära matrisen.
Hursomhelst, det var en trevlig övning. Förvänta dig frågan ”DFS on binary array without recursion and stack” på din nästa intervju.
- algoritmer
- datastrukturer
- programmering
mishadoff 10 september 2017
Lämna ett svar