Egenvektor

Eigenvektorer är en speciell uppsättning vektorer som är förknippade med ett linjärt system av ekvationer (dvs.e., en matrisekvation) som ibland också kallas karakteristiska vektorer, egentliga vektorer eller latenta vektorer (Marcus och Minc 1988, s. 144).

Bestämningen av ett systems egenvektorer och egenvärden är ytterst viktig inom fysik och teknik, där den är likvärdig med diagonalisering av matriser och förekommer i så vanliga tillämpningar som stabilitetsanalys, fysiken hos roterande kroppar och små svängningar hos vibrerande system, för att nämna bara några. Varje egenvektor är kopplad till ett motsvarande så kallat egenvärde. Matematiskt sett måste man skilja mellan två olika typer av egenvektorer: vänstra egenvektorer och högra egenvektorer. För många problem inom fysik och teknik är det dock tillräckligt att endast beakta högra egenvektorer. Termen ”egenvektor” som används utan förbehåll i sådana tillämpningar kan därför förstås som en hänvisning till en höger egenvektor.

Den nedbrytning av en kvadratisk matris i egenvärden och egenvektorer kallas i detta arbete för egendekomposition, och det faktum att denna nedbrytning alltid är möjlig så länge som matrisen som består av egenvektorerna i är kvadratisk är känd som teoremet om egendekomposition.

Definiera en höger egenvektor som en kolumnvektor som uppfyller

(1)

där är en matris, så

(2)

vilket innebär att de högra egenvärdena måste ha noll determinant, dvs.e.,

(3)

Samma sak gäller för att definiera en vänster egenvektor som en radvektor som uppfyller

(4)

Tar man transponeringen av varje sida får man

(5)

som kan skrivas om till

(6)

Rör om igen för att få

(7)

vilket innebär

(8)

Omskrivning ger

			(9)
			(10)
			(11)

där det sista steget följer av identiteten

(12)

Ekvation av ekvationerna (◇) och (11), som båda är lika med 0 för godtyckliga och , kräver därför att , dvs, vänstra och högra egenvärden är ekvivalenta, ett påstående som inte är sant för egenvektorer.

Låt vara en matris som bildas av kolumnerna för de högra egenvektorerna och vara en matris som bildas av raderna för de vänstra egenvektorerna. Låt

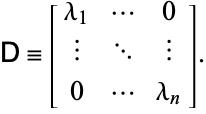(13)

Då

.

			(14)
			(15)

och

			(16)
			(17)

så

(18)

Men denna ekvation är av formen

.

(19)

där är en diagonalmatris, så det måste vara sant att också är diagonal. Om är en symmetrisk matris är vänster och höger egenvektorer helt enkelt varandras transponeringar, och om är en självadjungerad matris (dvs. den är hermitisk) är vänster och höger egenvektorer adjungerade matriser.

Eigenvektorer får inte vara lika med nollvektorn. En skalär multipel av en egenvektor som inte är noll är likvärdig med den ursprungliga egenvektorn. Därför är egenvektorer ofta normaliserade till enhetslängd.

En matris har alltid egenvärden, varav några eller alla kan vara degenererade, men en sådan matris kan ha mellan 0 och linjärt oberoende egenvektorer. Till exempel har matrisen endast den enda egenvektorn .

Eigenvektorer kan beräknas i Wolfram Language med hjälp av Eigenvectors. Detta kommando returnerar alltid en lista med längden , så alla egenvektorer som inte är linjärt oberoende returneras som nollvektorer. Egenvektorer och egenvärden kan returneras tillsammans med kommandot Eigensystem.

Givet en matris med egenvektorer , och och motsvarande egenvärden , och , kan en godtycklig vektor skrivas

(20)

Användning av matrisen ,

			(21)
			(22)

så

(23)

Om , och följer därför att

(24)

så upprepad tillämpning av matrisen på en godtycklig vektor resulterar på ett häpnadsväckande sätt i en vektor som är proportionell mot egenvektorn med största egenvärde.