mishadoff thoughts

Implementing Depth-First Search for the Binary Tree without stack and recursion.

Binary Tree Array

This is binary tree.

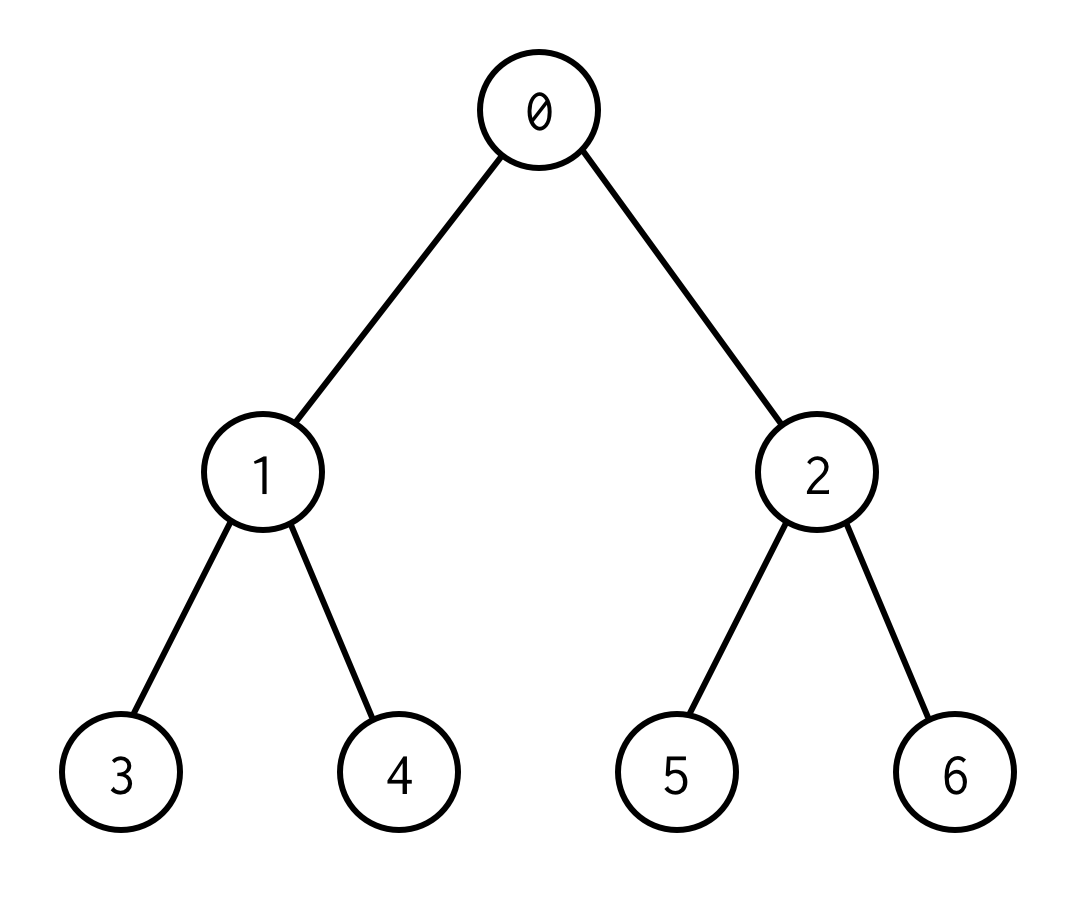
0 is a root node.
0 has two children: left 1 and right: 2.
Cada criança tem seus filhos e assim por diante.
Os nós sem filhos são nós foliares (3,4,5,6).

O número de bordas entre os nós raiz e folha define a altura da árvore. A árvore acima tem a altura 2.

A abordagem padrão para implementar árvore binária é definir a classe chamada BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

No entanto, há um truque para implementar árvore binária usando apenas arrays estáticos. Se você enumerar todos os nós na árvore binária por níveis começando de zero você pode empacotá-la em array.

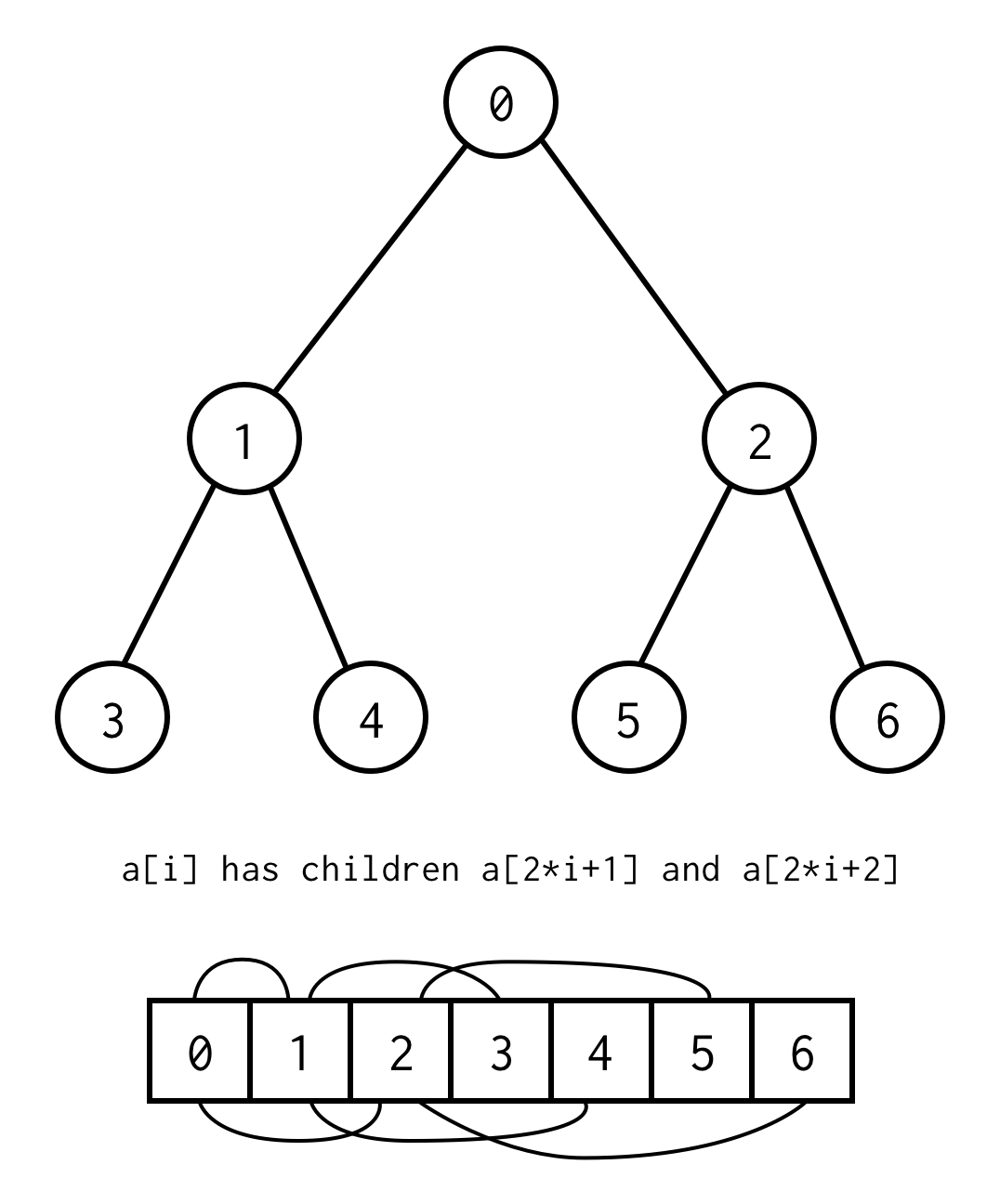
A relação entre o índice dos pais e o índice dos filhos, permite-nos passar de pai para filho, assim como da criança para pai

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Importante notar que a árvore deve ser completa, o que significa que para a altura específica ela deve conter exatamente elementos.

Você pode evitar tal exigência colocando null em vez de elementos ausentes. A enumeração ainda se aplica para nós vazios também. Isto deve cobrir qualquer árvore binária possível.

Aquela representação de array para árvore binária nós chamaremos Binary Tree Array.Nós sempre assumimos que ela conterá elementos.

BFS vs DFS

Existem dois algoritmos de busca para árvore binária: busca BFS (wide-first search) e busca DFS (depth-first search).

A melhor maneira de entendê-los é visualmente

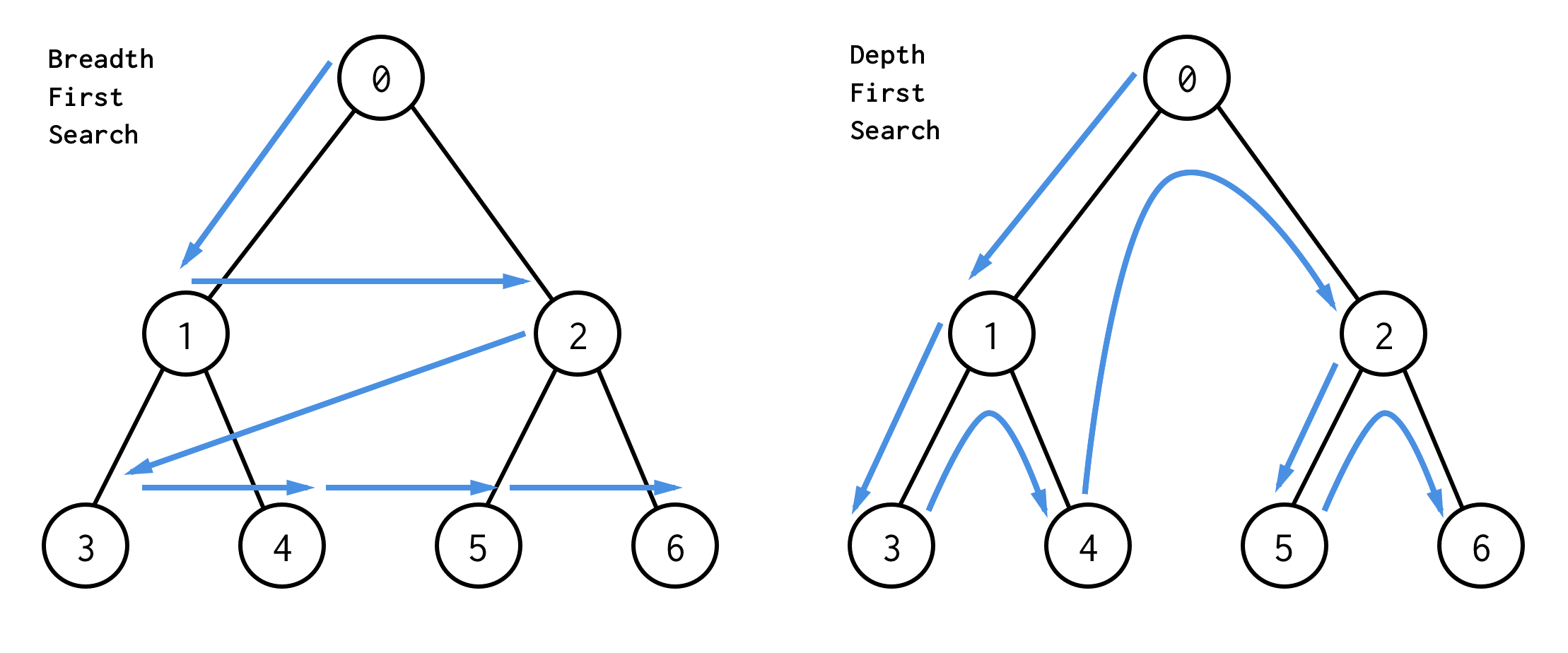
BFS busca nós nível por nível, começando a partir do nó raiz. Em seguida, verificar os seus filhos. Então filhos para filhos e assim por diante.Até que todos os nós sejam processados ou o nó que satisfaz a condição de pesquisa seja encontrado.

DFS comportam-se de forma diferente. Ele verifica todos os nós do caminho mais esquerdo da raiz até a folha, depois pula para cima e verifica o nó direito e assim por diante.

Para árvores binárias clássicas BFS implementadas usando a estrutura de dados Queue (LinkedList implementos Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Se você substituir queue pela pilha você terá a implementação DFS.

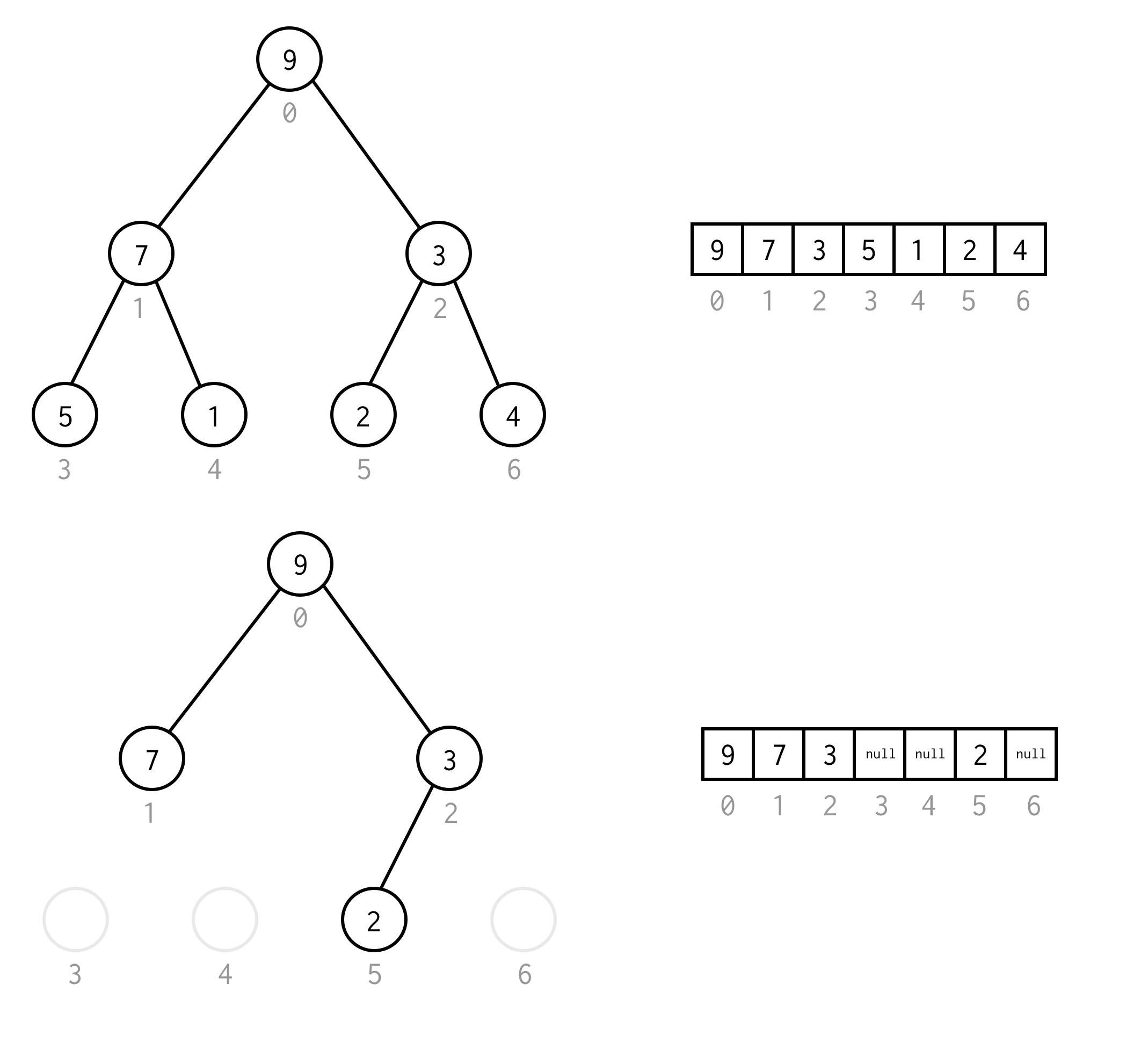
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Por exemplo, suponha que você precisa encontrar nó com valor 1 na seguinte árvore.

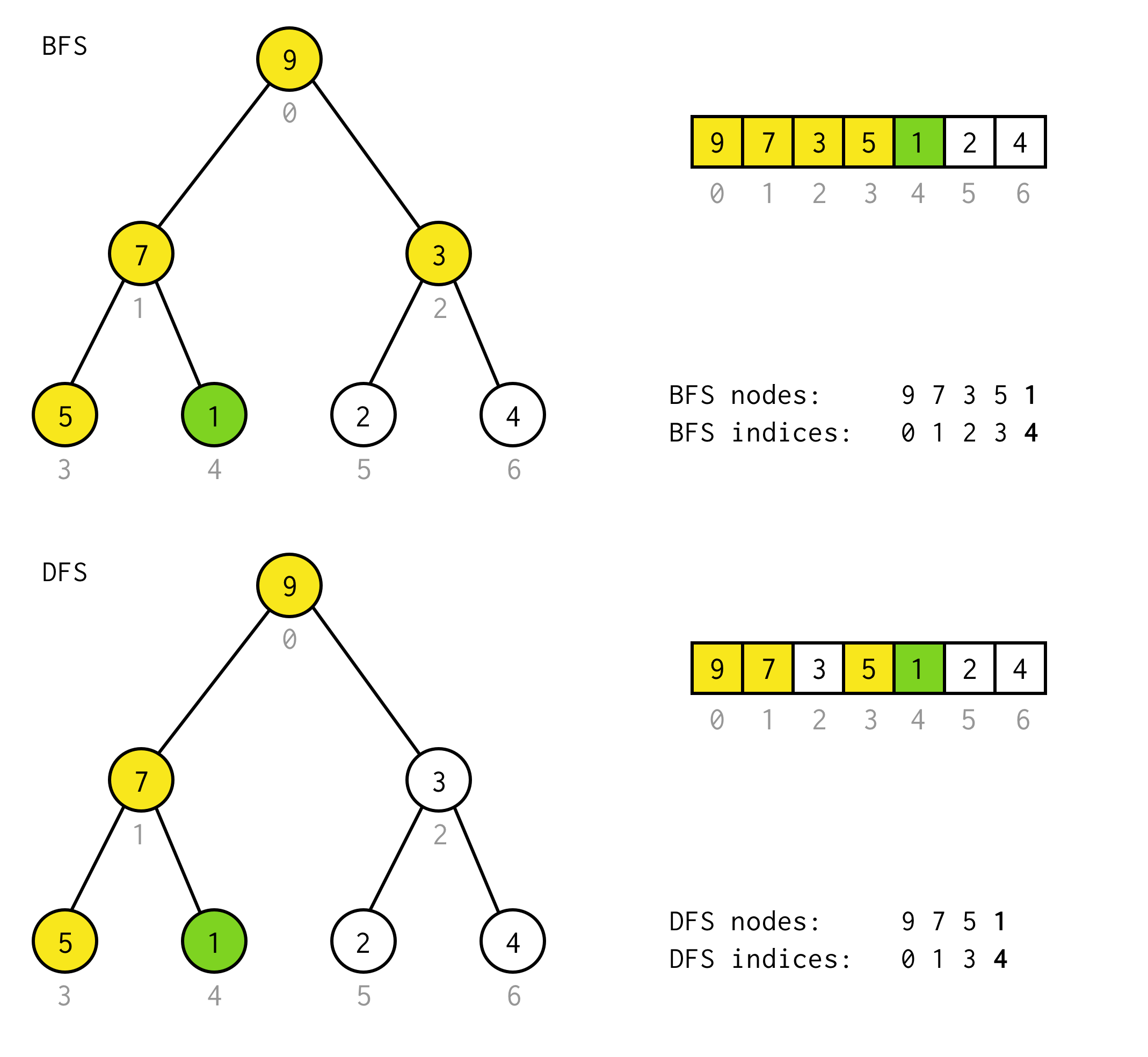
Célula amarela são células que são testadas no algoritmo de busca antes do nó necessário ser encontrado.Para alguns casos requer mais.

BFS e DFS para Binary Tree Array

Breadth-first search for binary tree array is trivial.Uma vez que os elementos em binary tree array são colocados nível por nível ebfs também está verificando elemento por nível, bfs para binary tree array é apenas uma busca linear

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

Depth-first search é um pouco mais difícil.

Usando a estrutura de dados da pilha, ela poderia ser implementada da mesma forma que para a árvore binária clássica, basta colocar índices na pilha.

A partir deste ponto a recorrência não é nada diferente, basta usar o método implícito call stack em vez da estrutura de dados stack.

E se pudéssemos implementar DFS sem pilha e recursividade.No final é apenas um índice correto de seleção em cada passo?

Bem, vamos tentar.

DFS para Binary Tree Array (sem pilha e recursividade)

Como em BFS nós começamos a partir do índice raiz 0.
Então precisamos inspecionar sua criança esquerda, cujo índice poderia ser calculado pela fórmula 2*i+1.
Passemos a chamar o processo de ir para a próxima criança esquerda dobrando.

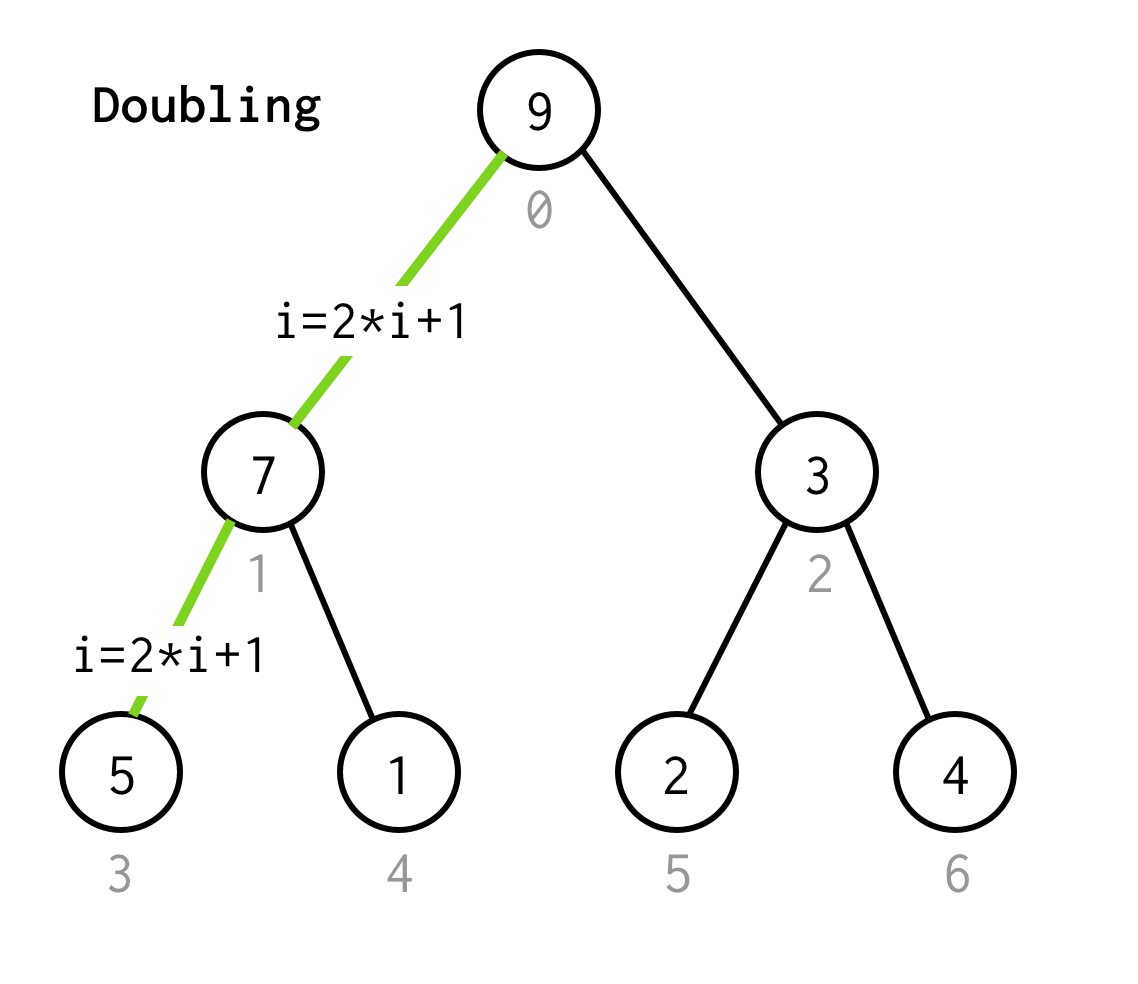
Continuamos dobrando o índice até não pararmos no nó foliar.

Então como podemos entender que é um nó foliar?

Se a próxima criança esquerda produzir índice fora dos limites da matriz, exceção, precisamos parar de dobrar e pular para a criança direita.

É uma solução válida, mas podemos evitar a duplicação desnecessária.A observação aqui é o número de elementos na árvore de alguns height é duas vezes maior (e mais um) do que a árvore com height - 1.

Para árvore com height = 2 temos 7 elementos, para árvore com height = 3 temos 7*2+1 = 15 elementos.

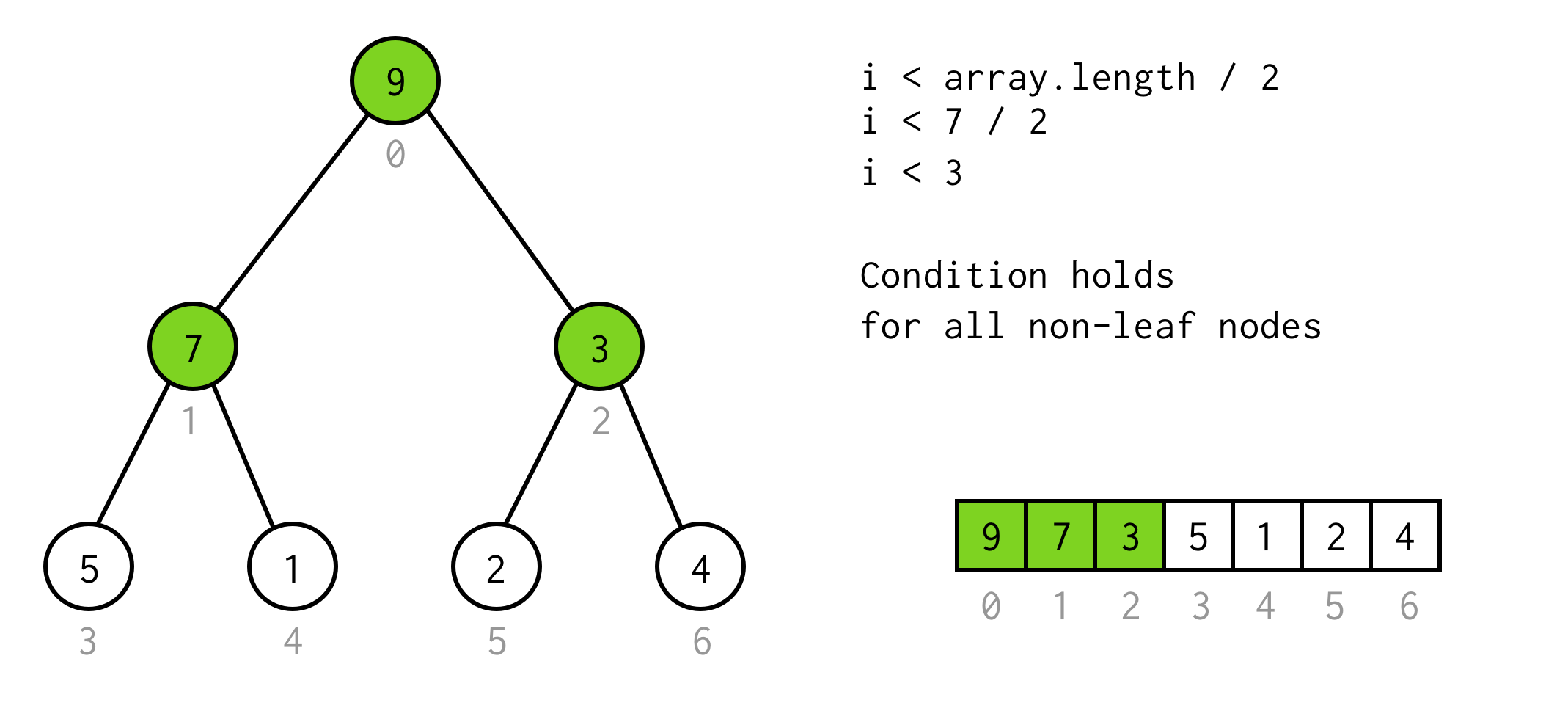
Usando esta observação construímos uma condição simples

i < array.length / 2

Você pode verificar se esta condição é válida para qualquer nó não-folha na árvore.

>

Nice até agora. Podemos correr dobrando, e até sabemos quando parar.Mas desta forma podemos verificar apenas os filhos que ficaram dos nós.

Quando ficamos presos no nó da folha e não podemos mais aplicar a dobra, realizamos a operação de salto.Basicamente, se dobrar é ir para a criança esquerda, o salto é ir para os pais e ir para a criança direita.

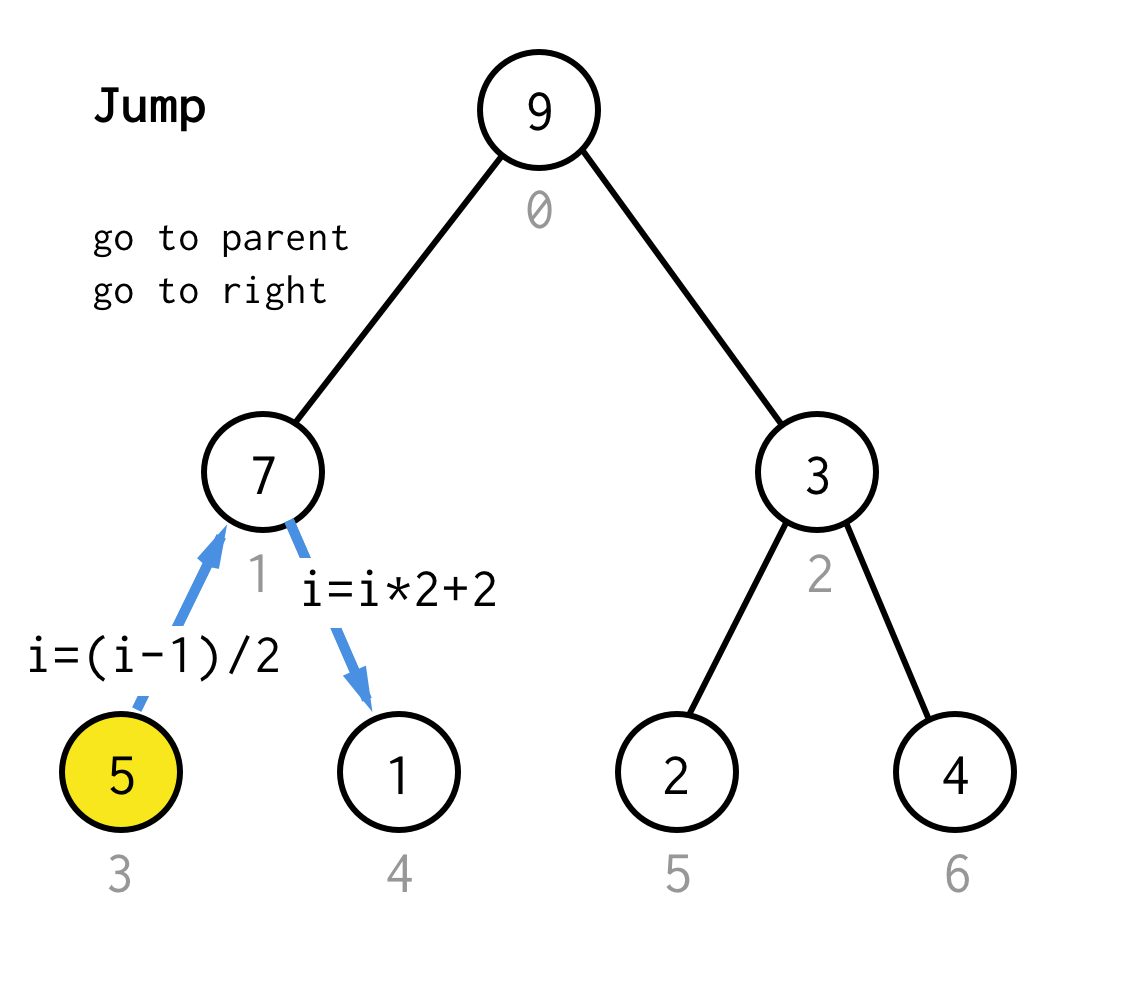
Tal operação de salto pode ser implementada apenas incrementando o índice da folha.Mas quando ficamos presos no próximo nó da folha, o incremento não move o nó para o próximo nó, necessário para o DFS.Então precisamos fazer salto duplo

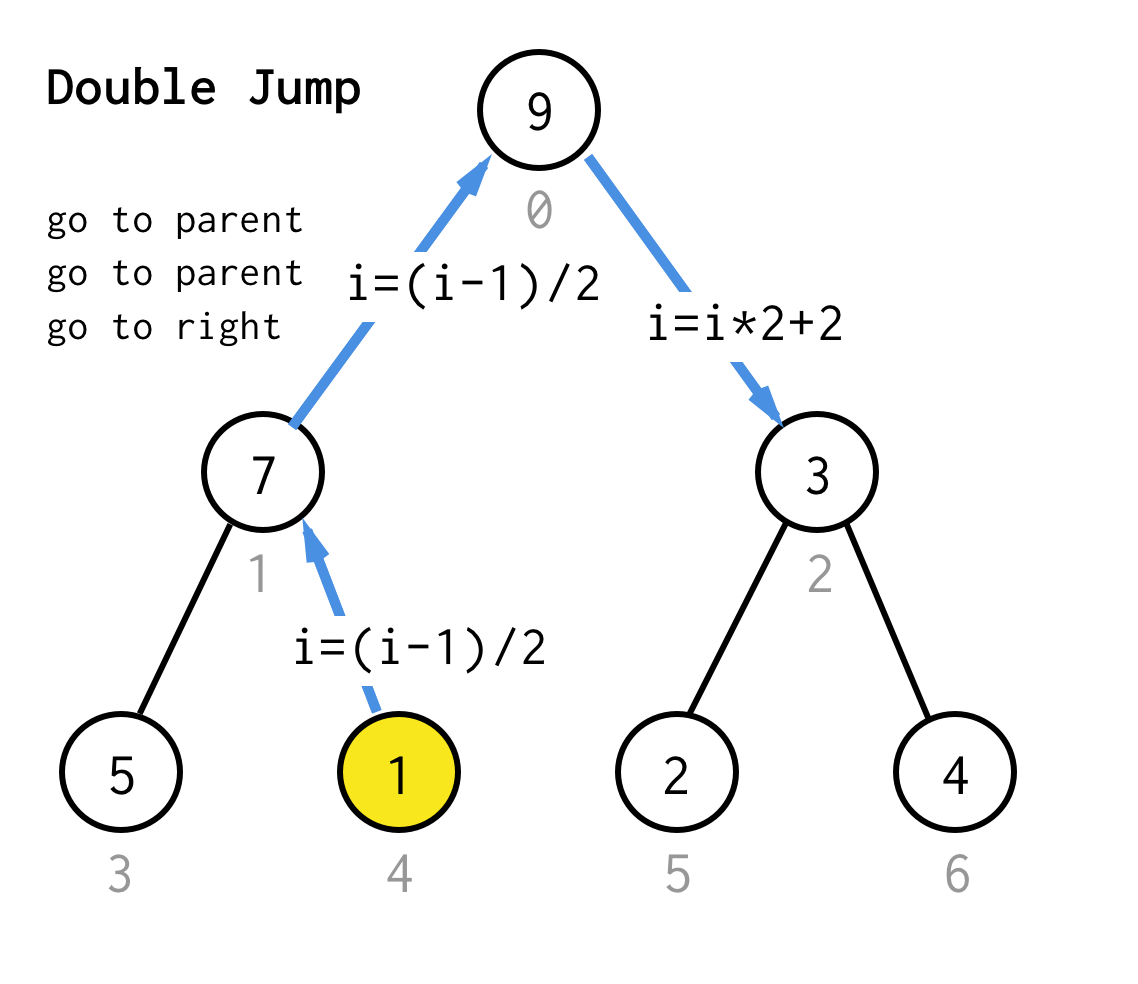
Make it more generic, para o nosso algoritmo poderíamos definir a operação de salto N, que especifica quantos saltos para o pai ele precisa e termina sempre com um salto para a criança certa.

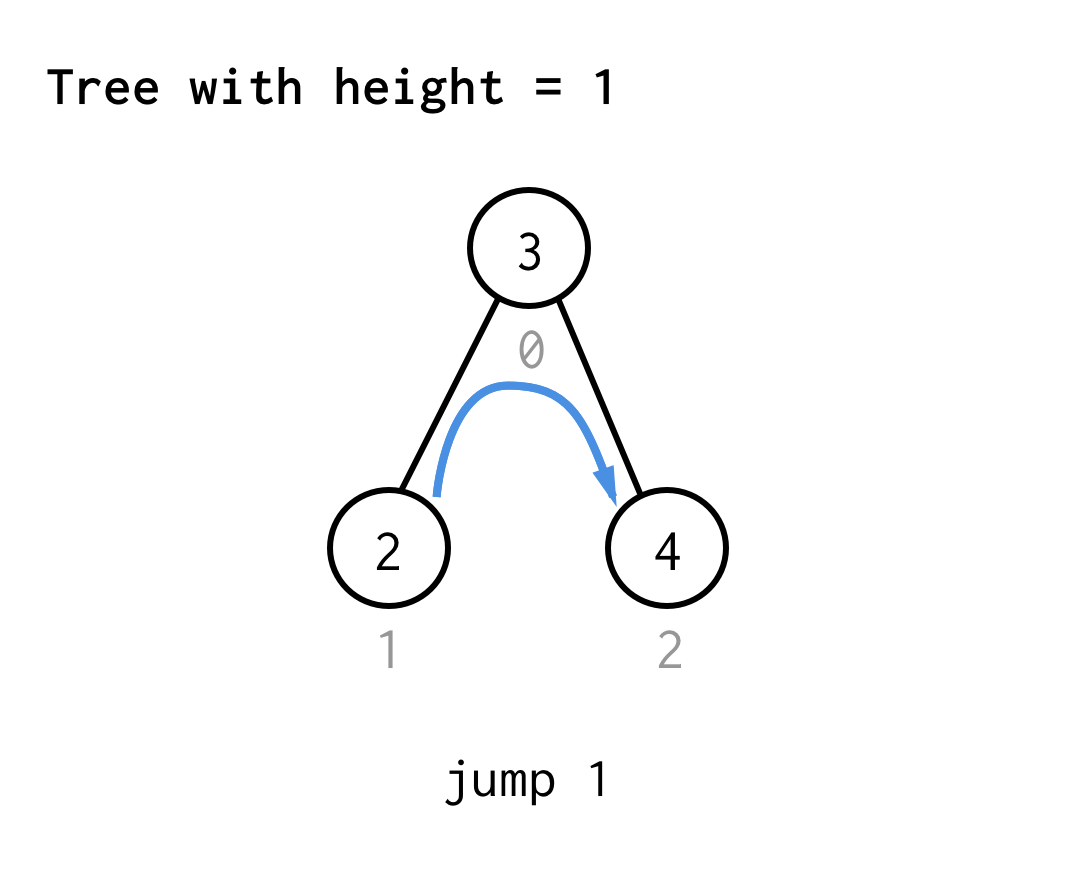
Para a árvore com altura 1, precisamos de um salto, salto 1

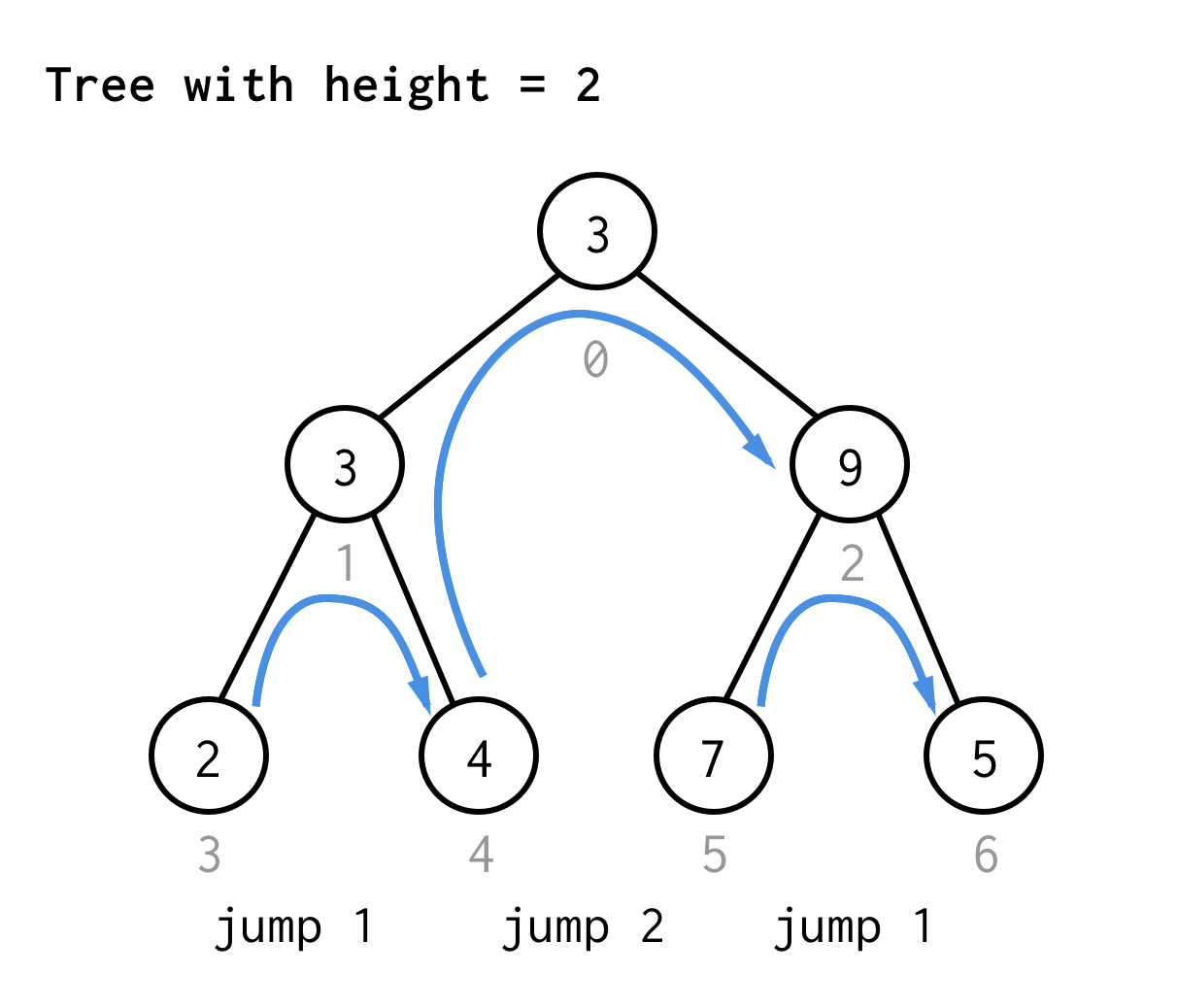
Para a árvore com altura 2, precisamos de um salto, um salto duplo, e um salto novamente

Para a árvore com altura 3, você pode aplicar as mesmas regras e obter 7 saltos.

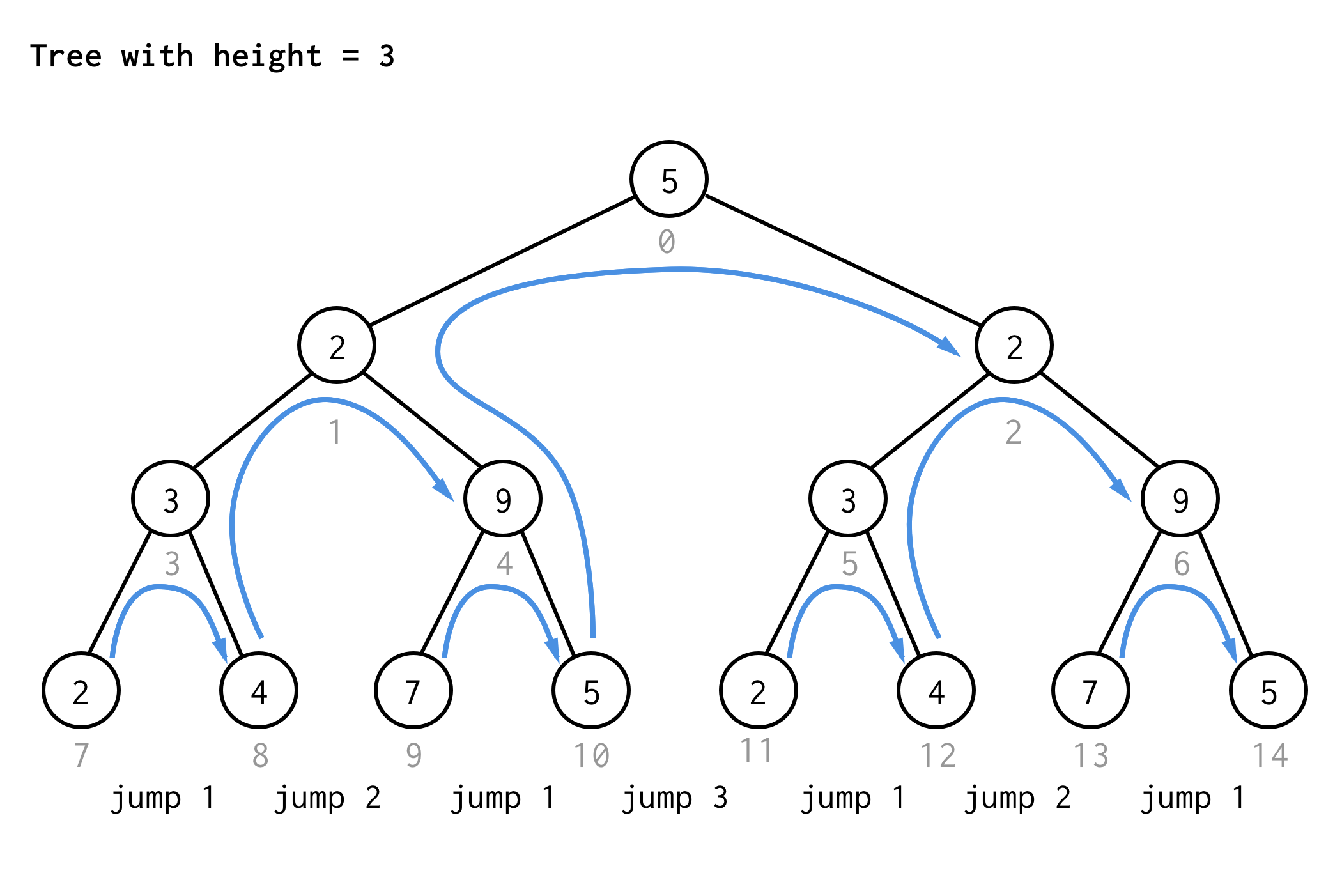
Ver o padrão?

Se você aplicar a mesma regra à árvore com altura 4 e escrever apenas valores de salto você obterá a próxima sequência de números

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Esta sequência conhecida como palavras Zimin e tem definição recursiva, o que não é ótimo, pois não é permitido o uso de recursividade.

Vamos encontrar outra maneira de calculá-la.

Se você olhar cuidadosamente a sequência de salto, você pode ver o padrão não recursivo.

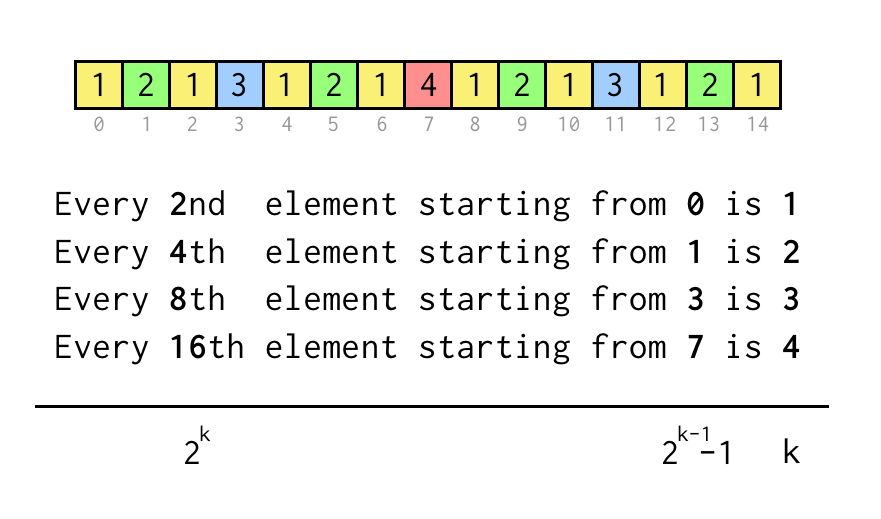
Nós podemos rastrear índice para a folha atual j, que corresponde ao índice na matriz de seqüência acima.

Para verificar declarações como “Cada 8º elemento a partir de 3” nós apenas verificamos j % 8 == 3, se são verdadeiros três saltos para o nó pai necessário.

O processo de salto iterativo será o seguinte

• Inicie com k = 1
• Pule uma vez para o nó pai aplicando i = (i - 1)/2
• Se leaf % 2*k == k - 1 todos os saltos realizados, saia
• Outros, defina k para 2*k e repita.

Se você juntar tudo o que discutimos

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Done. DFS para matriz de árvore binária sem pilha e recursividade

Complexidade

A complexidade parece quadrática porque temos loop em loop,mas vamos ver qual é a realidade.

• Para metade do total de nós (n/2) usamos estratégia de duplicação, que é constante O(1)
• Para a outra metade do total de nós (n/2) usamos estratégia de salto de folha.
• Metade dos nós de salto de folha (n/4) requer apenas um salto dos pais, 1 iteração. O(1)
• Metade desta metade (n/8) requer dois saltos, ou 2 iterações. O(1)
• …
• Apenas um nó de salto de folha requer um salto total para a raiz, que é O(logN)
• Então, se todos os casos tiverem O(1) excepto um que é O(logN), podemos dizer que a média para o salto é O(1)
• Total complexidade é O(n)

Desempenho

Apesar de a teoria ser boa, vamos ver como este algoritmo funciona na prática, comparando com outros.

Testamos 5 algoritmos, usando JMH.

• BFS em Árvore Binária (lista ligada como fila)
• BFS em Binary Tree Array (pesquisa linear)
• DFS em Árvore Binária (pilha)
• DFS em Binary Tree Array (stack)
• FDS interactivo em Binary Tree Array

Pré-criámos uma árvore e utilizámos um predicado para combinar com o último nó,para ter a certeza que atingimos sempre o mesmo número de nós para todos os algoritmos.

Então, resultados

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Obviamente, BFS em array vence. É apenas uma busca linear, então se você pode representar a árvore binária como array, faça-o.

FDS iterativa, que acabamos de descrever no artigo, levou 2e lugar e 4.5 vezes mais lento que a busca linear (BFS no array)

Os outros três algoritmos ainda mais lentos que a DFS iterativa, provavelmente, porque envolvem estruturas de dados adicionais, espaço extra e alocação de memória.

E o pior caso é BFS na árvore binária. Eu suspeito que aqui a lista ligada é um problema.

Conclusion

Binary Tree Array é um belo truque para representar estruturas de dados hierárquicos como um array estático (região contígua na memória). Ele define uma relação de índice simples para mover de pai para filho, bem como mover de filho para pai, o que não é possível com a representação clássica de array binário. Alguns inconvenientes, como inserção/eliminação lenta existe, mas tenho certeza que existem muitas aplicações para array de árvore binária.

Como temos mostrado, algoritmos de busca, BFS e DFS implementados em arrays são muito mais rápidos que seus irmãos em uma estrutura baseada em referência. Para problemas do mundo real não é tão importante, e, provavelmente, ainda vou usar o array binário baseado em referências.

Anyway, foi um bom exercício. Espere a pergunta “DFS em array binário sem recorrência e pilha” na sua próxima entrevista.

• algoritmos
• infra-estruturas de dados
• programação

mishadoff 10 de Setembro de 2017