Privacidade &Biscoitos
Este site usa cookies. Ao continuar, você concorda com o seu uso. Saiba mais, incluindo como controlar os cookies.
>
>
Uma espiral é uma curva que “emana de um ponto, afastando-se mais à medida que gira em torno do ponto”.
 >
>Existem muitos tipos diferentes de espirais, dependendo das fórmulas que as criam. Neste post de blog, vou discutir espirais bidimensionais (note que também existe uma variedade de espirais tridimensionais).
Espiral Arquimedeana
Esta é uma espiral com o nome do famoso matemático grego Arquimedes, que foi o primeiro a descrevê-la em seu livro Sobre Espirais. É descrita pela seguinte equação polar:
onde a e b são números reais.
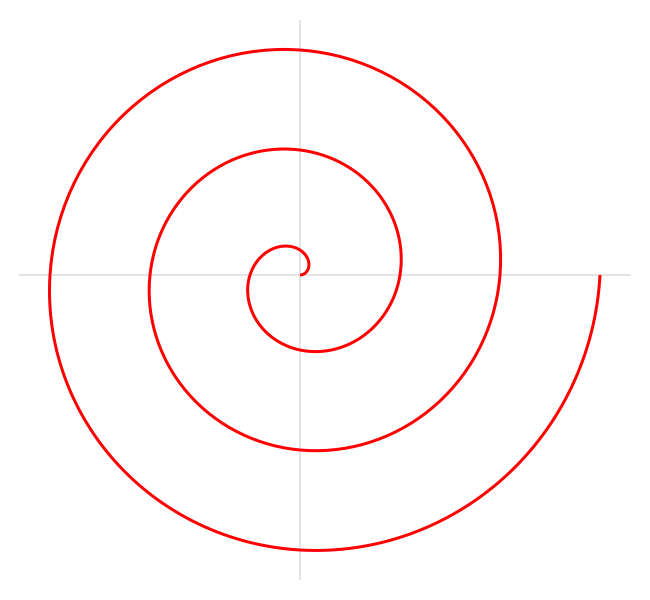
Ao mudar o parâmetro a a espiral irá girar e o parâmetro b controla a distância entre as sucessivas curvas.
Espiral de Fermat
A espiral de Fermat é uma espiral parabólica que obedece à seguinte equação polar:
É um tipo de espiral Arquimedeana.

Euler Spiral
Também conhecida como Espiral Cornu, é uma curva cuja curvatura cresce à medida que a distância da origem aumenta; “a curvatura de uma curva circular é igual ao recíproco do raio”.

A forma do parâmetro consiste em duas equações com intervalos de Fresnel, que só podem ser resolvidas aproximadamente.
Estas integrais, e portanto a espiral de Euler, podem ser usadas para descrever a distribuição de energia da difração de Fresnel em uma única fenda na teoria das ondas.
Espiral hiperbólica
Primeiro concebido por Pierre Varignon em 1704, a espiral hiperbólica é uma curva transcendental, significando que “é uma função analítica que não satisfaz uma equação polinomial”. É o oposto de uma espiral arquimédica e portanto tem a seguinte equação polar:
No centro, está a uma distância infinita do pólo; para θ começando em 0, r começa em infinito.
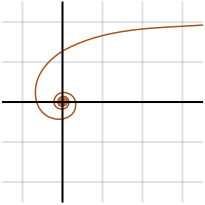
Lituus
O lituus é uma espiral com uma equação polar:
>
onde k é uma constante. Portanto, o ângulo é inversamente proporcional ao quadrado do raio. 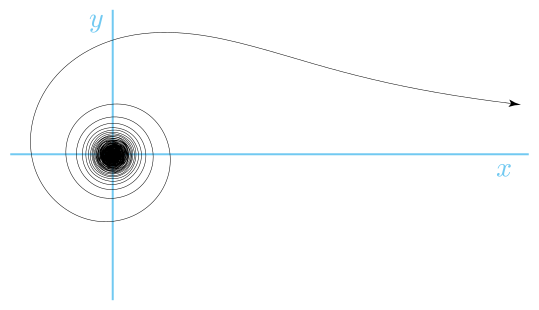
A curva recebeu o nome do antigo lituus romano (uma vara augural curva ou trombeta de guerra) por Roger Cotes numa colecção de artigos publicados em 1722.
Espiral Logarítmica
 A espiral logarítmica é uma espiral auto-similar, que aparece frequentemente na natureza. Foi inicialmente descrita por Descartes, mas foi estudada em profundidade por Jacob Bernoulli que a chamou de “a espiral maravilhosa”. Ela tem uma equação polar de
A espiral logarítmica é uma espiral auto-similar, que aparece frequentemente na natureza. Foi inicialmente descrita por Descartes, mas foi estudada em profundidade por Jacob Bernoulli que a chamou de “a espiral maravilhosa”. Ela tem uma equação polar de





Deixe uma resposta