Eigenvector

Álgebra > Álgebra Linear > Matrizes > Valores Eigenvector Matrix >

Álgebra > Álgebra Linear > Matrizes > Matriz Decomposição >

Vetores próprios são um conjunto especial de vetores associados a um sistema linear de equações (i.e., uma equação matricial) que às vezes também são conhecidos como vetores característicos, vetores próprios ou vetores latentes (Marcus e Minc 1988, p. 144).

A determinação dos vetores próprios e valores próprios de um sistema é extremamente importante em física e engenharia, onde é equivalente à diagonalização matricial e surge em aplicações tão comuns como a análise de estabilidade, a física de corpos rotativos e pequenas oscilações de sistemas vibratórios, para citar apenas algumas. Cada autovector é emparelhado com um valor próprio correspondente. Matematicamente, dois tipos diferentes de autovectores devem ser distinguidos: autovectores esquerdo e autovectores direito. Entretanto, para muitos problemas em física e engenharia, é suficiente considerar apenas os autovetores corretos. O termo “vetor próprio” usado sem qualificação em tais aplicações pode, portanto, ser entendido como referindo-se a um vetor próprio direito.

A decomposição de uma matriz quadrada em valores próprios e vetores próprios é conhecida neste trabalho como decomposição própria, e o fato de que esta decomposição é sempre possível desde que a matriz que consiste nos vetores próprios de seja quadrada é conhecida como o teorema da decomposição própria.

Definir um vector próprio direito como um vector de coluna satisfazendo

(1)

>onde é uma matriz, so

(2)

o que significa que os autovalores certos devem ter valor zero determinante, i.e.,

(3)

Similiarmente, defina um vector próprio esquerdo como um vector de linha satisfazendo

(4)

Passar a transposição de cada lado dá

(5)

que pode ser reescrito como

(6)

Reorganizar novamente para obter

(7)

o que significa

(8)

Rewriting gives

			(9)
			(10)
			(11)

onde o último passo segue da identidade

(12)

Equação de equações (◇) e (11), ambas iguais a 0 para arbitrárias e , portanto requer que , ou seja os autovalores esquerdo e direito são equivalentes, uma afirmação que não é verdadeira para os autovectores.

Let ser uma matriz formada pelas colunas dos autovectores direito e ser uma matriz formada pelas filas dos autovectores esquerdo. Let

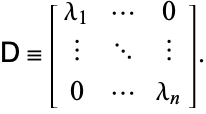(13)

>Então

			(14)
			(15)

			(16)
			(17)

(18)

Mas esta equação é da forma

(19)

where é uma matriz diagonal, então deve ser verdade que também é diagonal. Em particular, se é uma matriz simétrica, então os autovectores esquerdo e direito são simplesmente transpostos um pelo outro, e se é uma matriz auto-ajusta (isto é, é hermitiano), então os autovectores esquerdo e direito são matrizes adjuntas.

Os autovectores podem não ser iguais ao vector zero. Um múltiplo escalar não zero de um autovetor é equivalente ao autovetor original. Assim, sem perda de generalidade, os autovectores são frequentemente normalizados para o comprimento da unidade.

Embora uma matriz tenha sempre valores próprios, alguns ou todos eles podem ser degenerados, tal matriz pode ter entre 0 e autovectores linearmente independentes. Por exemplo, a matriz tem apenas o único autovetor .

Eigenvectors podem ser computados na Linguagem Wolfram usando Eigenvectors. Este comando sempre retorna uma lista de comprimento , então quaisquer autovectores que não são linearmente independentes são retornados como vetores zero. Vetores próprios e valores próprios podem ser retornados juntos usando o comando Eigensystem.