Vecteur propre

Les vecteurs propres sont un ensemble spécial de vecteurs associés à un système linéaire d’équations (i.e., une équation matricielle) qui sont parfois aussi appelés vecteurs caractéristiques, vecteurs propres ou vecteurs latents (Marcus et Minc 1988, p. 144).

La détermination des vecteurs propres et des valeurs propres d’un système est extrêmement importante en physique et en ingénierie, où elle équivaut à la diagonalisation de la matrice et se pose dans des applications courantes comme l’analyse de la stabilité, la physique des corps en rotation et les petites oscillations des systèmes vibrants, pour n’en citer que quelques-unes. Chaque vecteur propre est associé à une valeur propre correspondante. Mathématiquement, il faut distinguer deux types de vecteurs propres : les vecteurs propres gauches et les vecteurs propres droits. Toutefois, pour de nombreux problèmes de physique et d’ingénierie, il est suffisant de ne considérer que les vecteurs propres droits. Le terme « vecteur propre » utilisé sans qualification dans ces applications peut donc être compris comme désignant un vecteur propre droit.

La décomposition d’une matrice carrée en valeurs propres et vecteurs propres est connue dans cet ouvrage sous le nom de décomposition propre, et le fait que cette décomposition est toujours possible tant que la matrice constituée des vecteurs propres de est carrée est connu sous le nom de théorème de décomposition propre.

Définir un vecteur propre droit comme un vecteur colonne satisfaisant

(1)

où est une matrice, donc

(2)

ce qui signifie que les valeurs propres droites doivent avoir un déterminant nul, c’est-à-dire.e.,

(3)

De même, définissons un vecteur propre gauche comme un vecteur ligne satisfaisant

(4)

Prendre la transposition de chaque côté donne

(5)

qui peut être réécrit comme

(6)

Réorganisez à nouveau pour obtenir

(7)

ce qui signifie

(8)

La réécriture donne

			(9)
			(10)
			(11)

où la dernière étape découle de l’identité

(12)

L’équation (◇) et (11), qui sont toutes deux égales à 0 pour des et arbitraires, nécessite donc que , c’est-à-dire, les valeurs propres de gauche et de droite sont équivalentes, une affirmation qui n’est pas vraie pour les vecteurs propres.

Disons que est une matrice formée par les colonnes des vecteurs propres de droite et est une matrice formée par les lignes des vecteurs propres de gauche. Soit

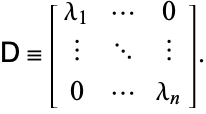(13)

Alors

.

			(14)
			(15)

et

.

			(16)
			(17)

so

(18)

Mais cette équation est de la forme

.

(19)

où est une matrice diagonale, donc il doit être vrai que est aussi diagonale. En particulier, si est une matrice symétrique, alors les vecteurs propres gauche et droit sont simplement les transposés l’un de l’autre, et si est une matrice auto-adjointe (c’est-à-dire qu’elle est hermitienne), alors les vecteurs propres gauche et droit sont des matrices adjointes.

Les vecteurs propres peuvent ne pas être égaux au vecteur zéro. Un multiple scalaire non nul d’un vecteur propre est équivalent au vecteur propre d’origine. Par conséquent, sans perte de généralité, les vecteurs propres sont souvent normalisés à la longueur unitaire.

Alors qu’une matrice a toujours valeurs propres, dont certaines ou toutes peuvent être dégénérées, une telle matrice peut avoir entre 0 et vecteurs propres linéairement indépendants. Par exemple, la matrice n’a que le seul vecteur propre .

Les vecteurs propres peuvent être calculés dans le Wolfram Language en utilisant Eigenvectors. Cette commande renvoie toujours une liste de longueur , donc tous les vecteurs propres qui ne sont pas linéairement indépendants sont renvoyés comme des vecteurs zéro. Les vecteurs propres et les valeurs propres peuvent être retournés ensemble en utilisant la commande Eigensystem.

Donné une matrice avec des vecteurs propres , , et et des valeurs propres correspondantes , , et , alors un vecteur arbitraire peut être écrit

(20)

Application de la matrice ,

			(21)
			(22)

so

(23)

Si , et , il s’ensuit donc que

(24)

donc l’application répétée de la matrice à un vecteur arbitraire donne étonnamment un vecteur proportionnel au vecteur propre ayant la plus grande valeur propre.