X

Privacité & Cookies

Ce site utilise des cookies. En continuant, vous acceptez leur utilisation. Apprenez-en plus, notamment comment contrôler les cookies.

Got It!

Publicités

Une spirale est une courbe qui « émane d’un point, s’éloignant au fur et à mesure qu’elle tourne autour du point ».

Il existe de nombreux types de spirales en fonction des formules qui les créent. Dans ce billet de blog, j’aborderai les spirales à deux dimensions (notez qu’il existe également une variété de spirales à trois dimensions).

Spirale d’Archimède

C’est une spirale nommée d’après le célèbre mathématicien grec Archimède, qui fut le premier à la décrire dans son livre Sur les spirales. Elle est décrite par l’équation polaire suivante :

\, r=a+b\theta

où a et b sont des nombres réels.

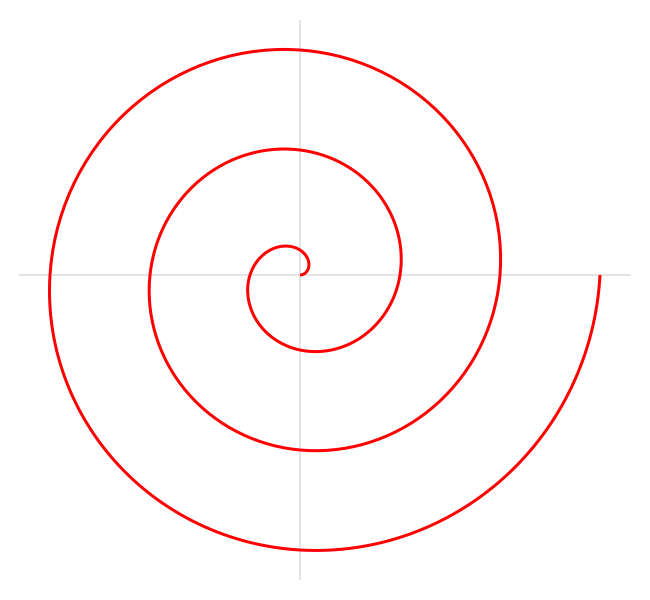
En changeant le paramètre a, la spirale tourne et le paramètre b contrôle la distance entre les tours successifs.

Spirale de Fermat

La spirale de Fermat est une spirale parabolique qui obéit à l’équation polaire suivante :

r=\pm \theta ^{1/2}\,

C’est un type de spirale d’Archimède.

Spirale d’Euler

Aussi appelée spirale de Cornu, c’est une courbe dont la courbure croît à mesure que la distance à l’origine augmente ; « la courbure d’une courbe circulaire est égale à l’inverse du rayon ».

La forme paramétrique est constituée de deux équations à intervalles de Fresnel, qui ne peuvent être résolues qu’approximativement.

S(x)=\int_0^x \sin(t^2)\,\mathrm{d}t,\quad C(x)=\int_0^x \cos(t^2)\,\mathrm{d}t.

Ces intégrales, et donc la spirale d’Euler, peuvent être utilisées pour décrire la distribution d’énergie de la diffraction de Fresnel à une fente unique dans la théorie des ondes.

Spirale hyperbolique

Pour la première fois conçue par Pierre Varignon en 1704, la spirale hyperbolique est une courbe transcendantale, ce qui signifie que « c’est une fonction analytique qui ne satisfait pas une équation polynomiale ». Elle est l’inverse d’une spirale d’Archimède et a donc l’équation polaire suivante :

r={\frac {a}{\theta }}

Au centre, elle est à une distance infinie du pôle ; pour θ commençant à 0, r commence à l’infini.

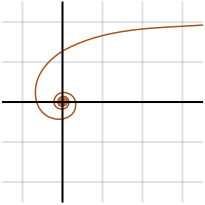
Lituus

Le lituus est une spirale dont l’équation polaire est :

r^2\theta = k \2001>

où k est une constante. Ainsi, l’angle est inversement proportionnel au carré du rayon.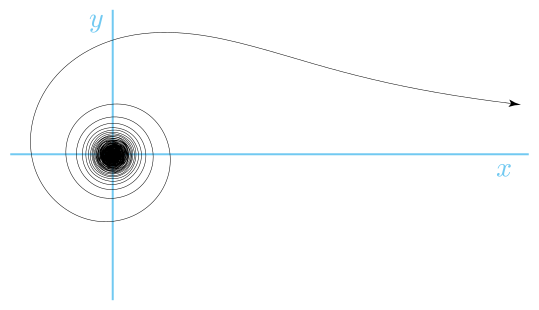

La courbe a été nommée d’après l’ancien lituus romain (un bâton augural courbé ou trompette de guerre) par Roger Cotes dans un recueil de documents publiés en 1722.

Spirale logarithmique

La spirale logarithmique est une spirale autosimilaire, qui apparaît souvent dans la nature. Elle fut décrite pour la première fois par Descartes, mais fut étudiée en profondeur par Jacob Bernoulli qui l’appela « la merveilleuse spirale ». Elle a une équation polaire de