Propriétés des angles d’un triangle

Thèmes connexes:
Plus de leçons de géométrie
Fiches de travail de géométrie
Jeux de géométrie
Dans ces leçons, nous donnerons un résumé des propriétés des angles d’un triangle.

• Théorème de la somme des triangles – La somme des 3 angles d’un triangle est toujours de 180°
• La somme d’un angle intérieur et de son angle extérieur adjacent est de 180°
• Théorème des angles extérieurs – Un angle extérieur d’un triangle est égal à la somme des deux angles intérieurs opposés
• Un triangle équilatéral a 3 angles égaux qui font 60° chacun. Un triangle isocèle a 2 angles égaux, qui sont les angles opposés aux 2 côtés égaux

Les angles d’un triangle ont les propriétés suivantes :

Propriété 1 : Théorème de la somme des triangles

La somme des 3 angles d’un triangle est toujours de 180°.

Exemple :

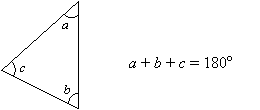
Comment prouver le théorème de la somme des triangles ?
La vidéo suivante montre comment prouver que la somme des angles d’un triangle est de 180 degrés. (Théorème de la somme des triangles)

• Afficher les solutions étape par étape

Comment trouver l’angle manquant dans un triangle en utilisant le théorème de la somme des triangles?
Étape 1 : Écrire l’équation en ajoutant tous les angles et en les rendant égaux à 180°.
Etape 2 : Résolvez pour x.
Etape 3 : Substituez pour trouver les angles manquants.

• Afficher les solutions étape par étape

Propriété 2:

La somme d’un angle intérieur et de son angle extérieur adjacent est de 180°.

Exemple :

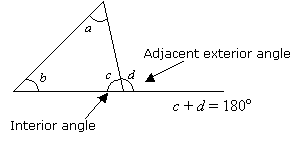
Propriété 3 : Théorème des angles extérieurs

Un angle extérieur d’un triangle est égal à la somme des deux angles intérieurs opposés.

Exemple :

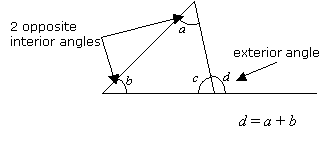
Angles extérieurs d’un triangle
Définition de l’angle inconnu d’un triangle
Exemple:
1. Evaluez le triangle abc, où a = 40° et b = 60°. Quel est l’angle extérieur à ∠acb?
2. Evaluez le triangle abc, où a = 50° et b = 30°. Quel est l’angle extérieur de ∠acb?
2. Evaluez le triangle abc, où a = 90° et b = 40°. Quel est l’angle extérieur à ∠acb?

• Afficher les solutions pas à pas

Comment utiliser le théorème de l’angle extérieur pour résoudre des problèmes impliquant des angles dans un triangle?

• Afficher les solutions pas à pas

Propriété 4 :

Un triangle équilatéral a 3 angles égaux qui font 60° chacun.
Un triangle isocèle a 2 angles égaux, qui sont les angles opposés aux 2 côtés égaux.
Comment trouver l’angle manquant dans un triangle isocèle ?

• Afficher les solutions étape par étape

Lignes parallèles et théorème de la somme des angles des triangles

• Afficher les solutions étape par étape

Les propriétés des angles ci-dessus peuvent nous aider à trouver les angles inconnus dans un triangle.

Exemple:

Trouvez la valeur de x dans le triangle suivant.

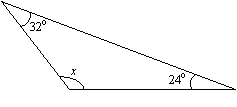
Solution :

x + 24° + 32° = 180° (la somme des angles est de 180°)
x + 56° = 180°
x = 180° – 56° = 124°

Exemple :

Trouvez les valeurs de x et y dans le triangle suivant.

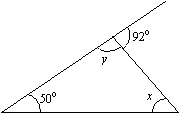
Solution :

x + 50° = 92° (somme des angles intérieurs opposés = angle extérieur)
x = 92° – 50° = 42°

y + 92° = 180° (angle intérieur + angle extérieur adjacent = 180°.)
y = 180° – 92° = 88°

Essayez la calculatrice gratuite Mathway et le résolveur de problèmes ci-dessous pour vous exercer à divers sujets mathématiques. Essayez les exemples donnés, ou tapez votre propre problème et vérifiez votre réponse avec les explications étape par étape.

.