Mise en œuvre de la recherche en profondeur pour l’arbre binaire sans pile et sans récursion.
Tableau d’arbre binaire
C’est un arbre binaire.
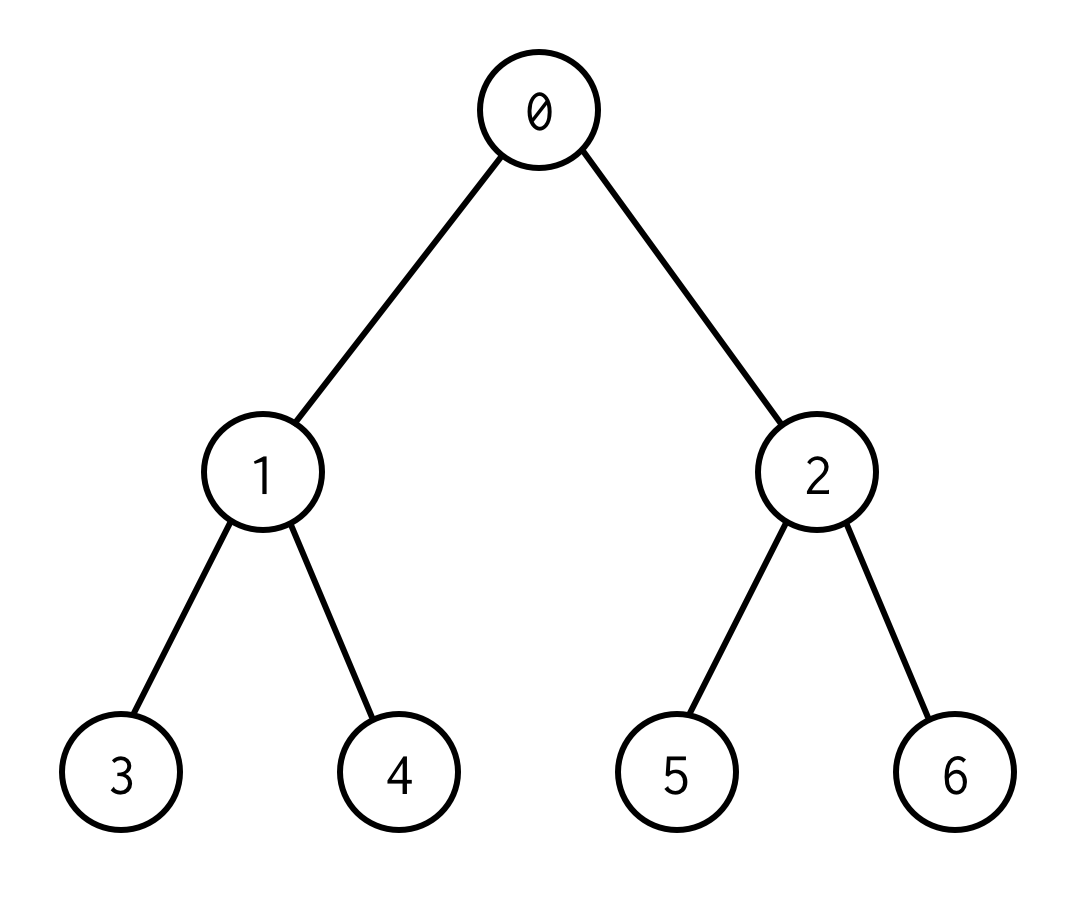
0 est un nœud racine.0 a deux enfants : gauche 1 et droite : 2.
Chacun de ses enfants a ses enfants et ainsi de suite.
Les nœuds sans enfants sont des nœuds feuilles (3,4,5,6).
Le nombre d’arêtes entre les nœuds racines et feuilles définissent la hauteur de l’arbre.L’arbre ci-dessus a la hauteur 2.
L’approche standard pour implémenter l’arbre binaire est de définir une classe appelée BinaryNode
public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}Cependant, il existe une astuce pour implémenter l’arbre binaire en utilisant uniquement des tableaux statiques.Si vous énumérez tous les nœuds de l’arbre binaire par niveaux à partir de zéro, vous pouvez l’emballer dans un tableau.
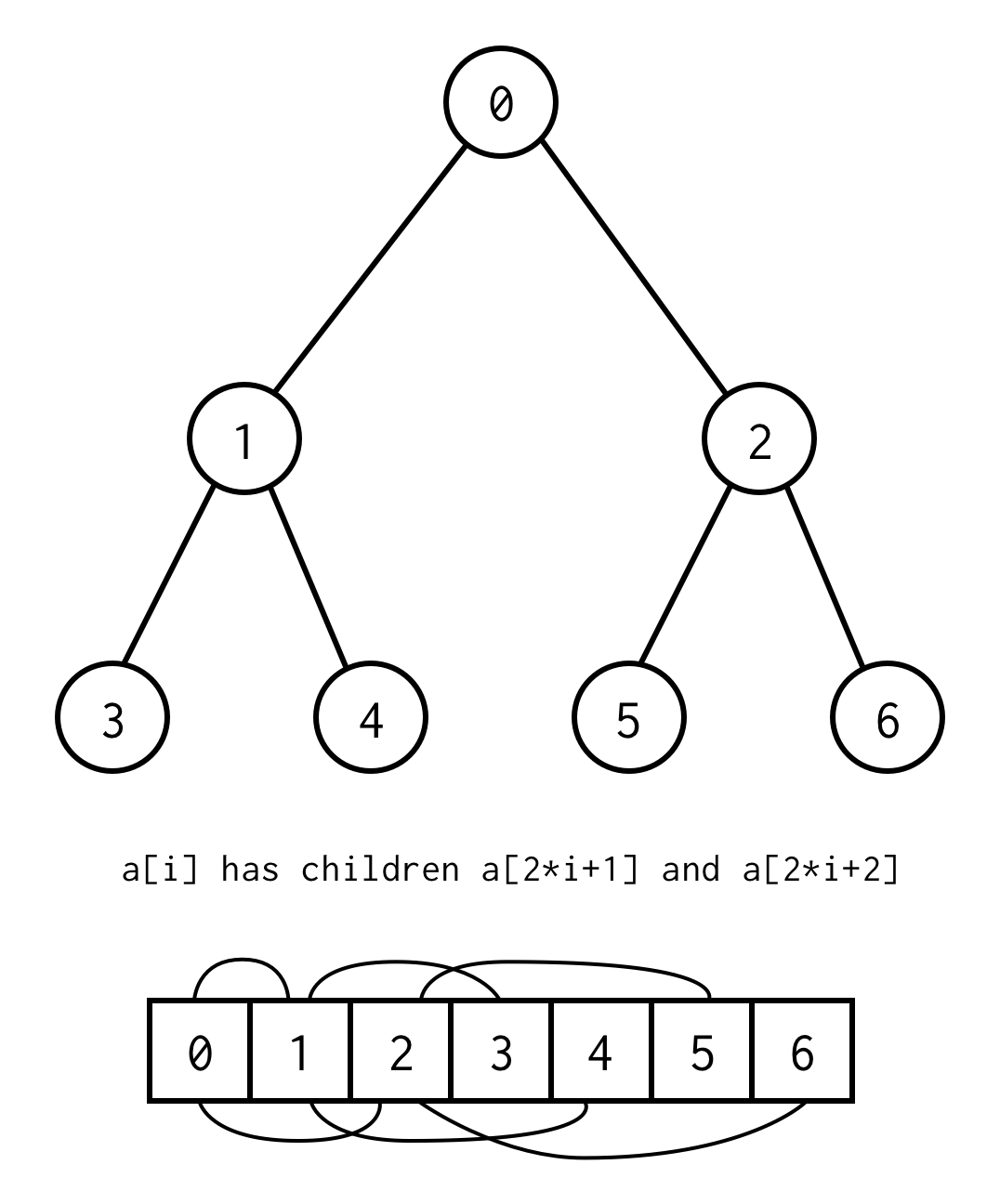
La relation entre l’indice du parent et l’indice de l’enfant,nous permet de passer du parent à l’enfant, ainsi que de l’enfant au parent
left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2Note importante que l’arbre doit être complet, ce qui signifie que pour la hauteur spécifique, il doit contenir exactement des éléments.
Vous pouvez éviter une telle exigence en plaçant null à la place des éléments manquants.L’énumération s’applique toujours aux nœuds vides également. Ceci devrait couvrir tout arbre binaire possible.
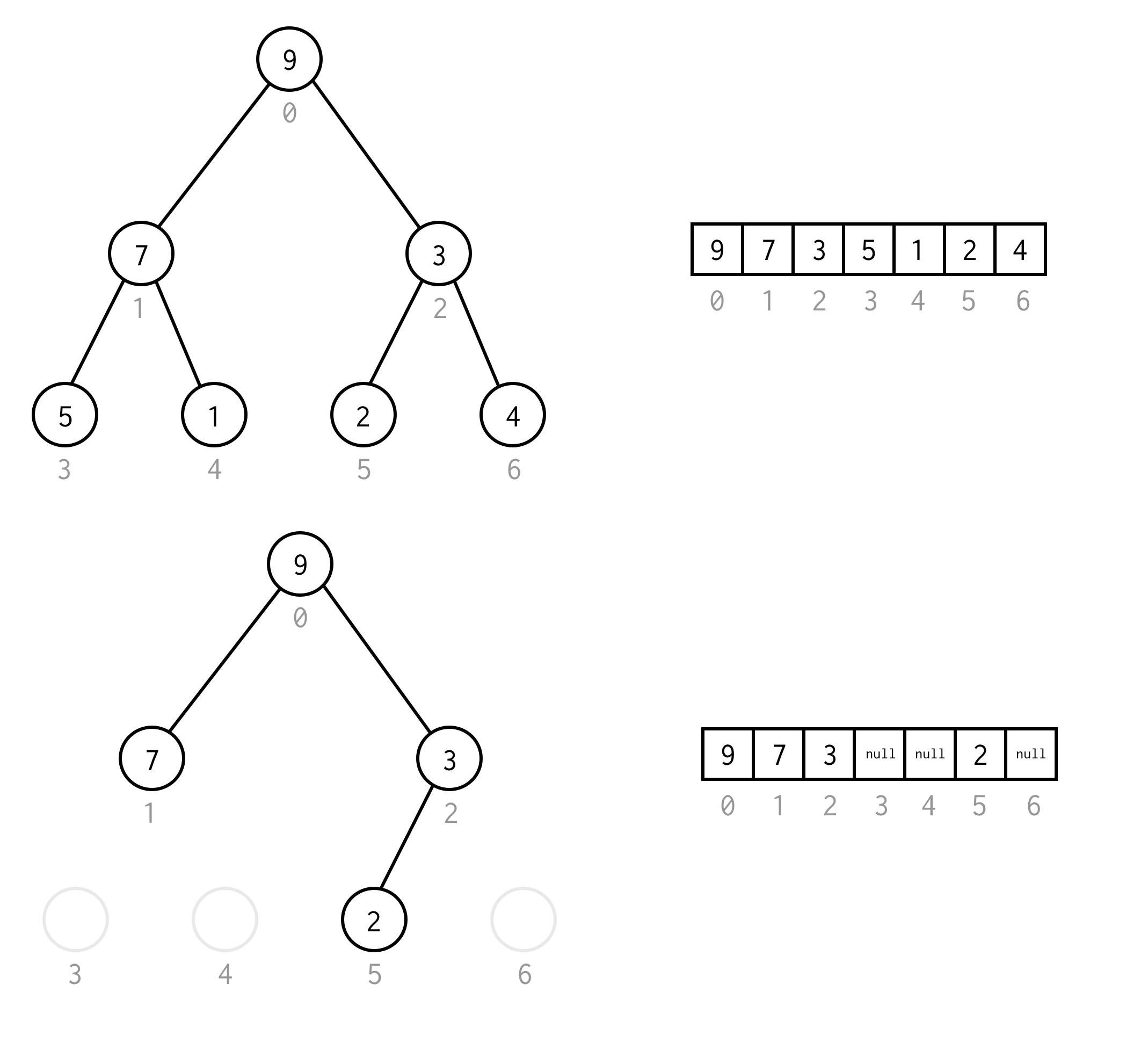
Cette représentation de tableau pour arbre binaire nous l’appellerons Tableau d’arbre binaire.Nous supposons toujours qu’il contiendra des éléments.
BFS vs DFS
Il existe deux algorithmes de recherche pour l’arbre binaire :la recherche en largeur (BFS) et la recherche en profondeur (DFS).
La meilleure façon de les comprendre est visuellement
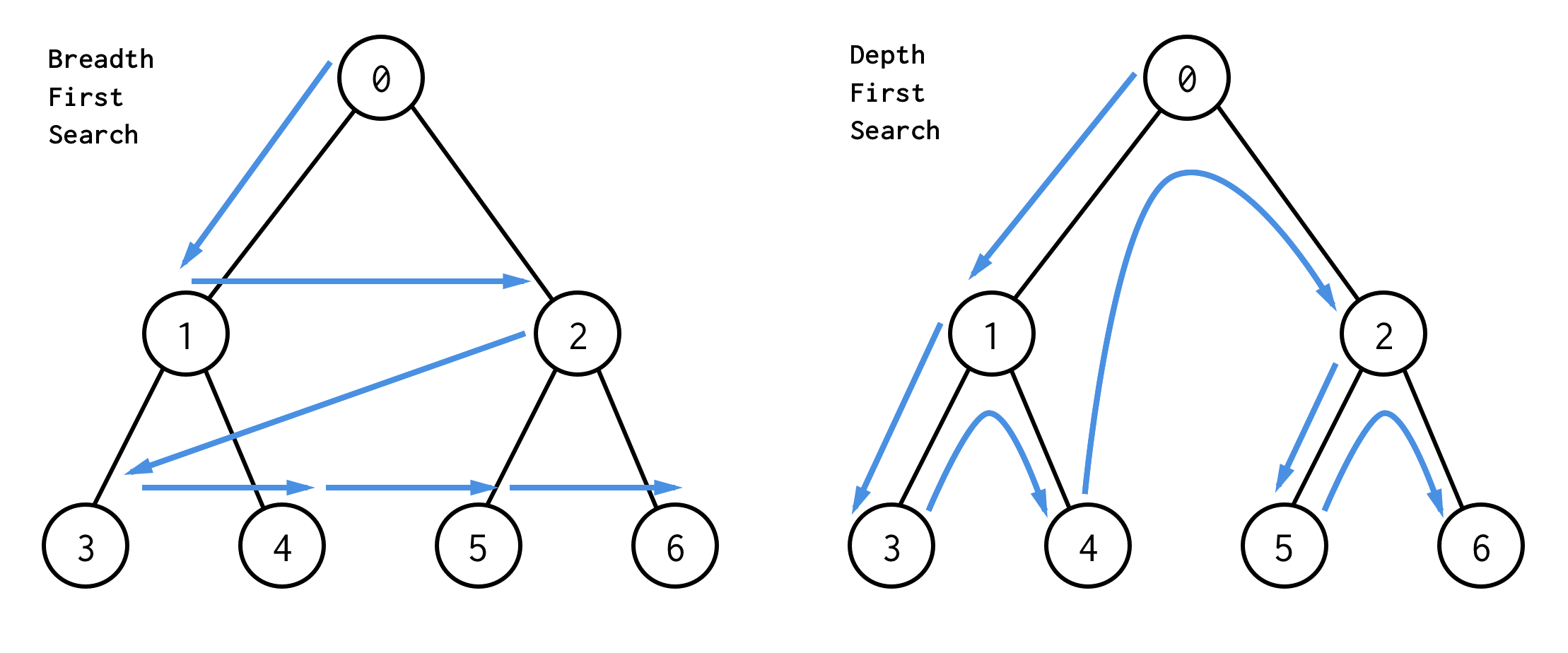
La BFS recherche les nœuds niveau par niveau, en commençant par le nœud racine. Puis en vérifiant ses enfants. Puis les enfants pour les enfants et ainsi de suite.Jusqu’à ce que tous les nœuds soient traités ou que le nœud qui satisfait la condition de recherche soit trouvé.
DFS se comporte différemment. Il vérifie tous les nœuds à partir du chemin le plus à gauche de la racine à la feuille,puis saute en haut et vérifie le nœud de droite et ainsi de suite.
Pour les arbres binaires classiques BFS implémenté en utilisant la structure de données Queue (LinkedList implémente Queue)
public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}Si vous remplacez queue par la pile vous obtiendrez l’implémentation DFS.
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}Par exemple, supposons que vous avez besoin de trouver le nœud avec la valeur 1 dans l’arbre suivant.
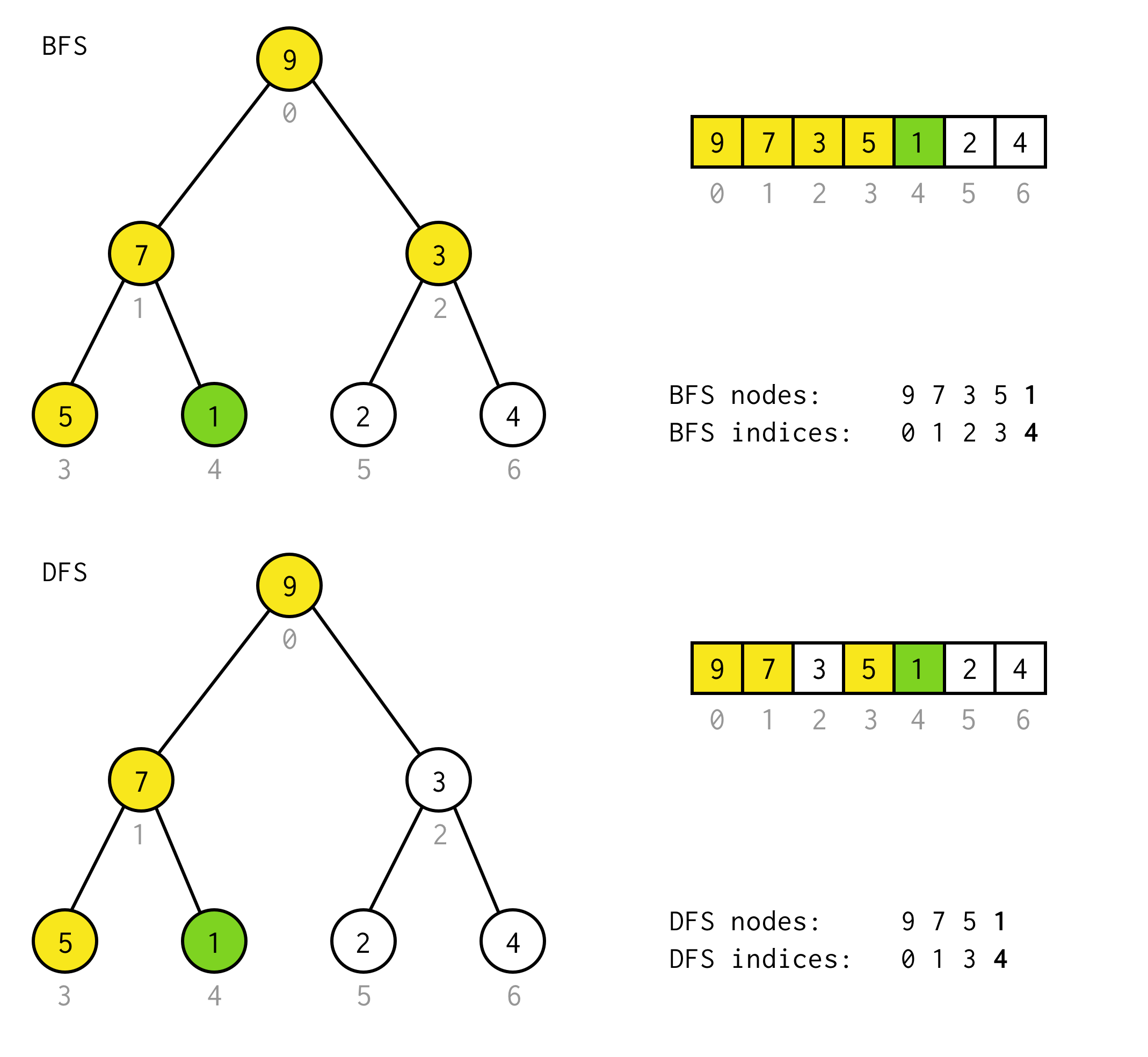
Les cellules jaunes sont des cellules qui sont testées dans l’algorithme de recherche avant le nœud nécessaire trouvé.Tenez compte du fait que pour certains cas, DFS nécessite moins de nœuds pour le traitement.Pour certains cas, il en nécessite plus.
BFS et DFS pour un tableau d’arbre binaire
La recherche en largeur-première pour un tableau d’arbre binaire est triviale.Puisque les éléments dans le tableau d’arbre binaire sont placés niveau par niveau et quebfs vérifie également l’élément niveau par niveau, bfs pour le tableau d’arbre binaire est juste une recherche linéaire
public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}La recherche en profondeur-première est un peu plus difficile.
En utilisant la structure de données pile, il pourrait être mis en œuvre de la même manière que pour l’arbre binaire classique, il suffit de mettre les indices dans la pile.
À partir de ce point, la récursion n’est pas différente du tout, vous utilisez juste la pile d’appel de méthode implicite au lieu de la pile de structure de données.
Et si nous pouvions mettre en œuvre le DFS sans pile et sans récursion.A la fin, c’est juste une sélection de l’indice correct à chaque étape ?
Eh bien, essayons.
DFS pour un tableau d’arbre binaire (sans pile et sans récursion)
Comme dans BFS, nous commençons à partir de l’indice racine 0.
Puis nous devons inspecter son enfant gauche, dont l’indice pourrait être calculé par la formule 2*i+1.
Appelons le processus d’aller au prochain enfant gauche le doublement.
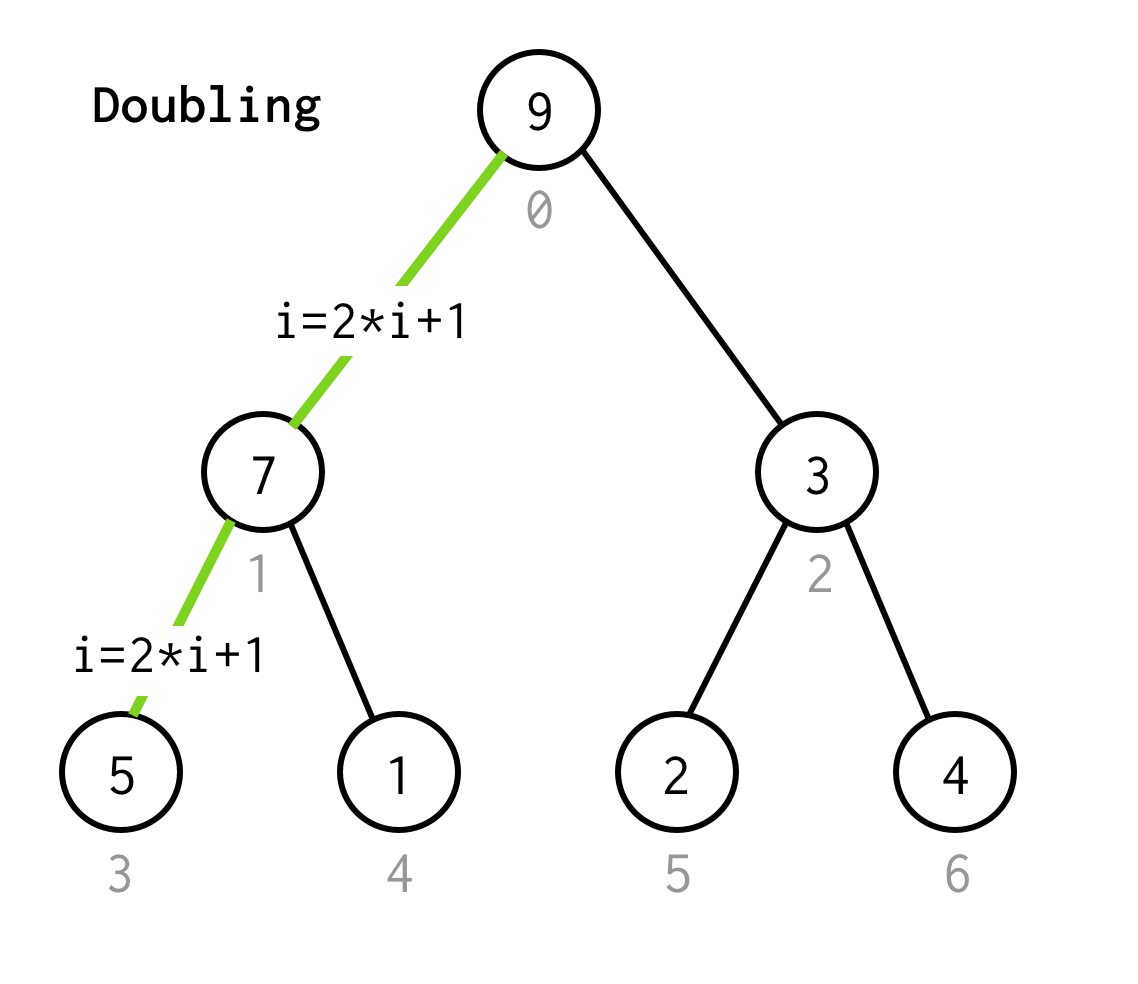
Nous continuons à doubler l’indice jusqu’à ce que nous ne nous arrêtions pas au nœud feuille.
Alors comment pouvons-nous comprendre que c’est un nœud feuille ?
Si l’enfant suivant de gauche produit un index hors des limites du tableau exceptionnellement, nous devons arrêter de doubler et sauter à l’enfant de droite.
C’est une solution valide, mais nous pouvons éviter le doublement inutile.L’observation ici est que le nombre d’éléments dans l’arbre de certains height est deux fois plus grand (et plus un)que l’arbre avec height - 1.
Pour l’arbre avec height = 2 on a 7éléments, pour l’arbre avec height = 3 on a 7*2+1 = 15éléments.
En utilisant cette observation on construit une condition simple
i < array.length / 2On peut vérifier que cette condition est valable pour tout nœud non feuille de l’arbre.
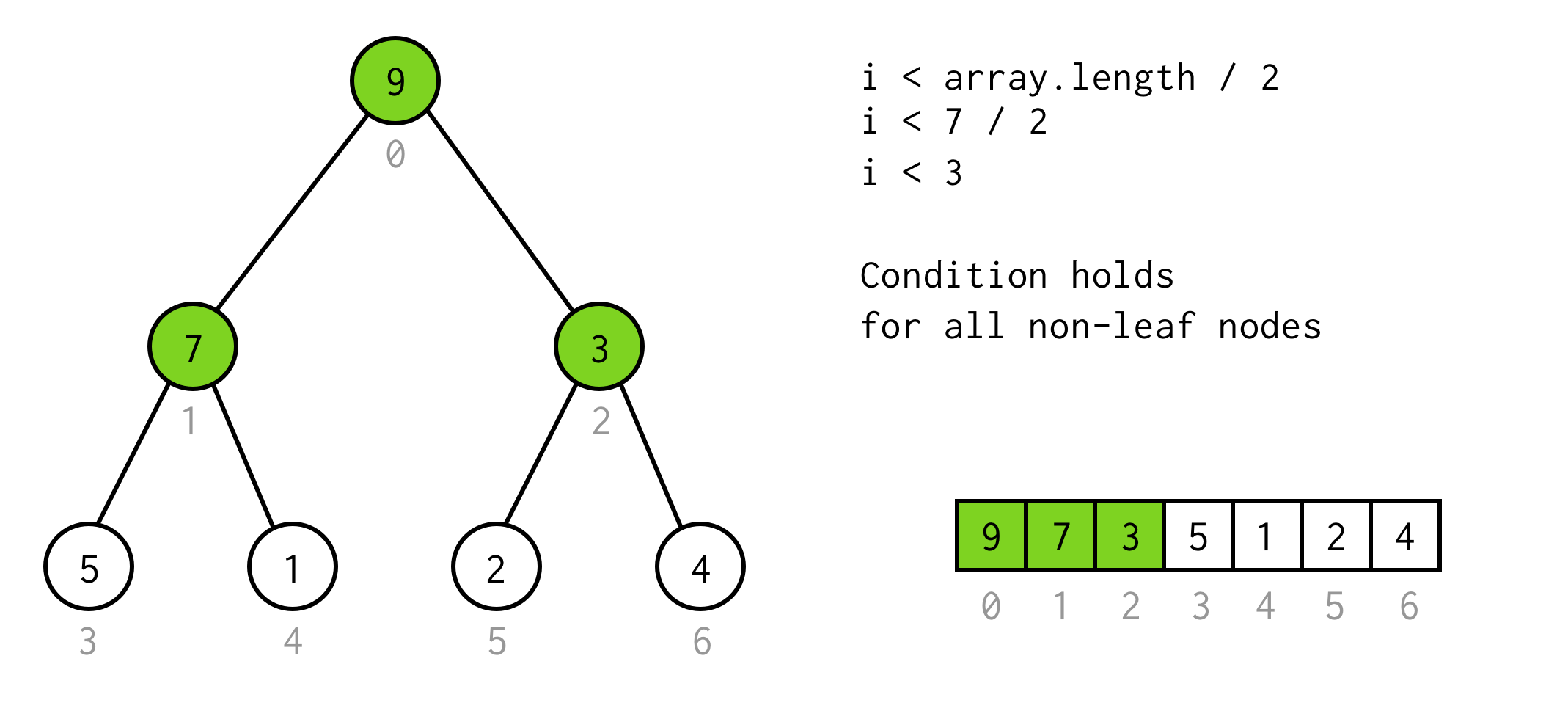
Bien jusque là. Nous pouvons exécuter le doublage, et nous savons même quand nous devons nous arrêter.Mais de cette façon, nous pouvons vérifier seulement les enfants gauches des nœuds.
Lorsque nous sommes bloqués au nœud feuille et que nous ne pouvons plus appliquer le doublage, nous effectuons une opération de saut.Fondamentalement, si le doublage est d’aller à l’enfant gauche, le saut est d’aller au parent et d’aller à l’enfant droit.
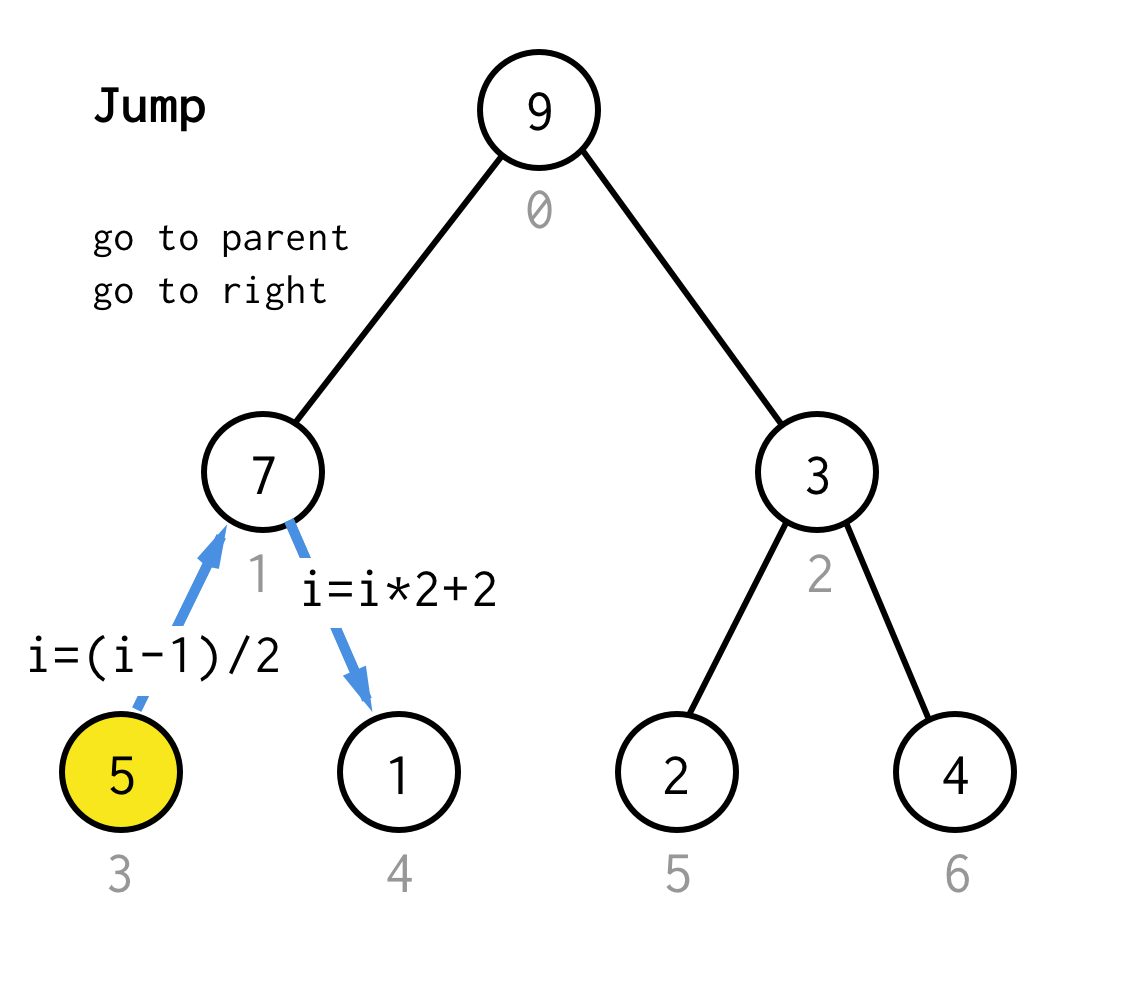
Cette opération de saut peut être mise en œuvre en incrémentant simplement l’index de la feuille.Mais quand nous sommes coincés au prochain nœud de feuille, l’incrémentation ne déplace pas le nœud au prochain nœud, requis pour DFS.Donc nous devons faire un double saut
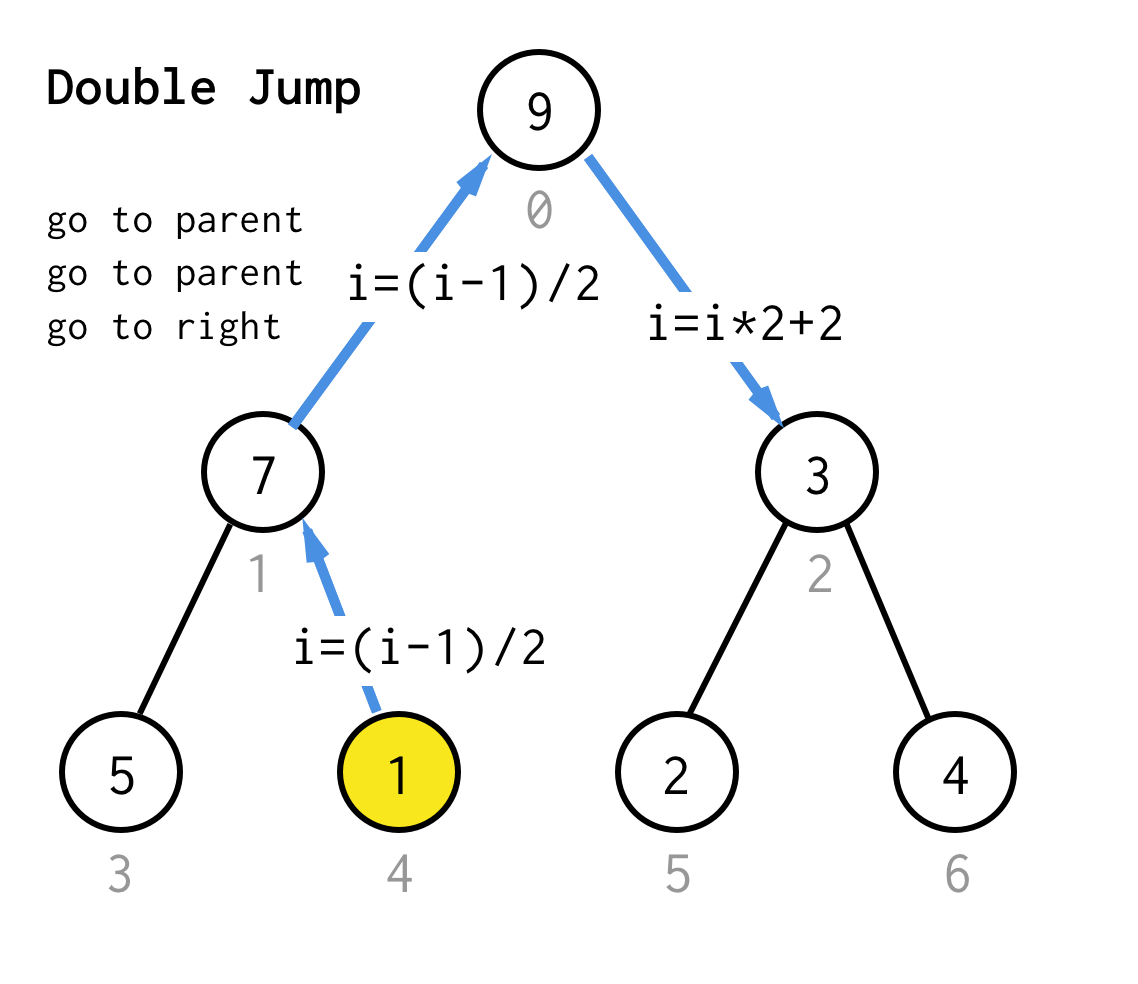
Pour le rendre plus générique, pour notre algorithme nous pourrions définir l’opération saut N, qui spécifie combien de sauts vers le parent il nécessite et se termine toujours par un saut vers le bon enfant.
Pour l’arbre de hauteur 1, nous avons besoin d’un saut, le saut 1
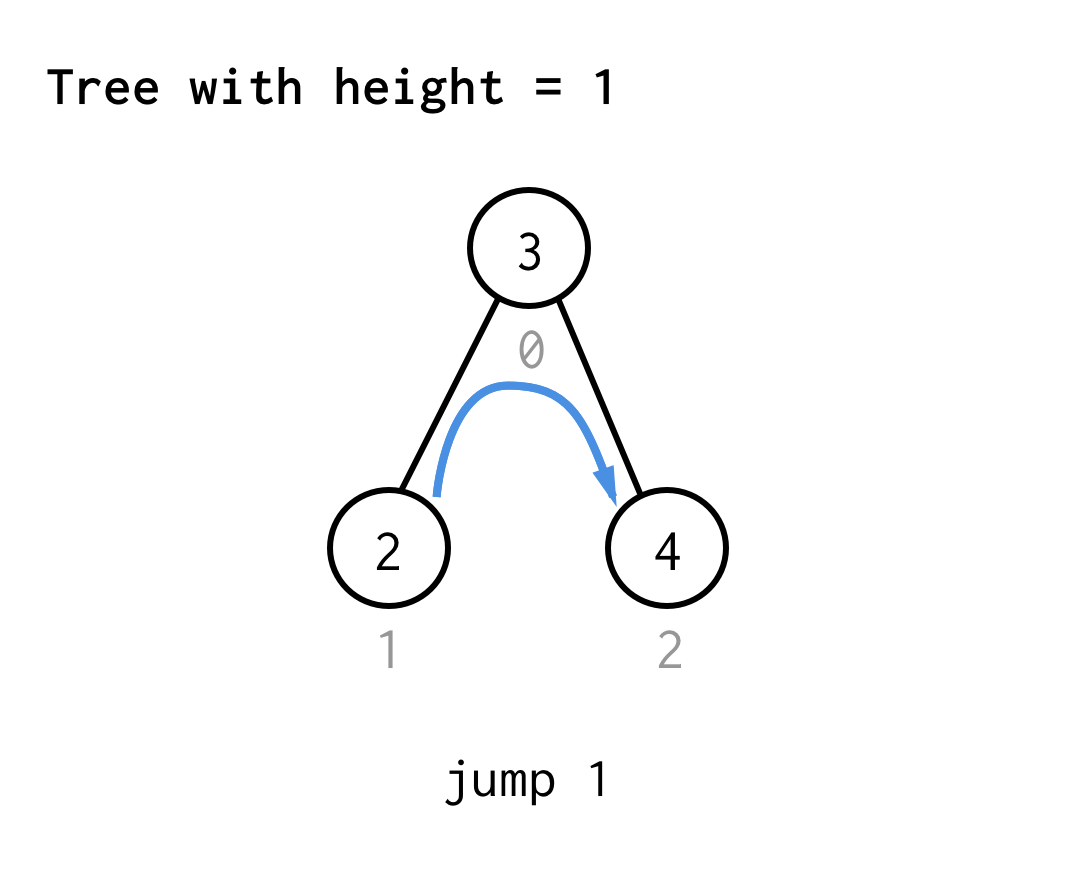
Pour l’arbre de hauteur 2, nous avons besoin d’un saut, d’un double saut, et qu’un saut encore
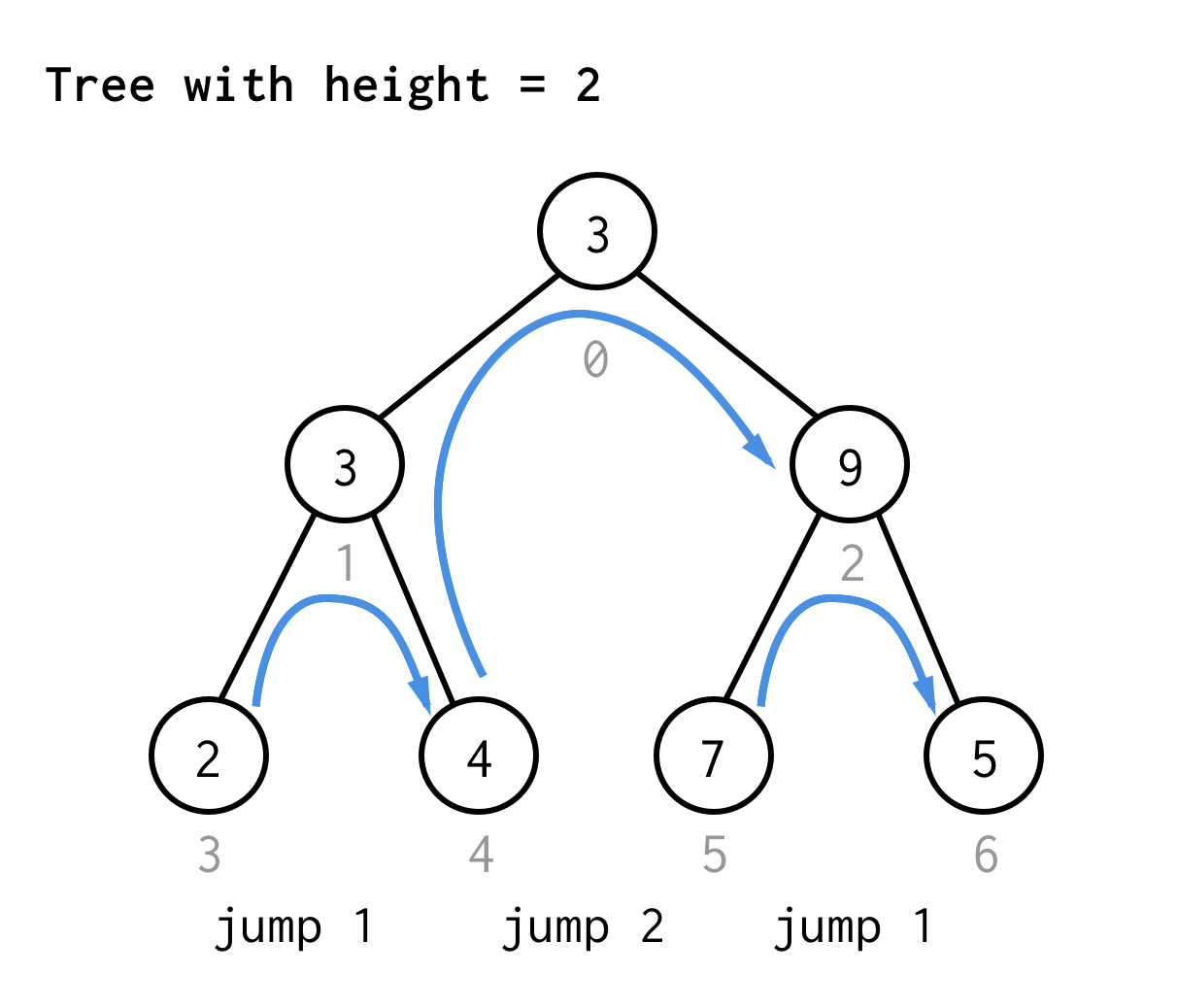
Pour l’arbre de hauteur 3, on peut appliquer les mêmes règles et obtenir 7 sauts.
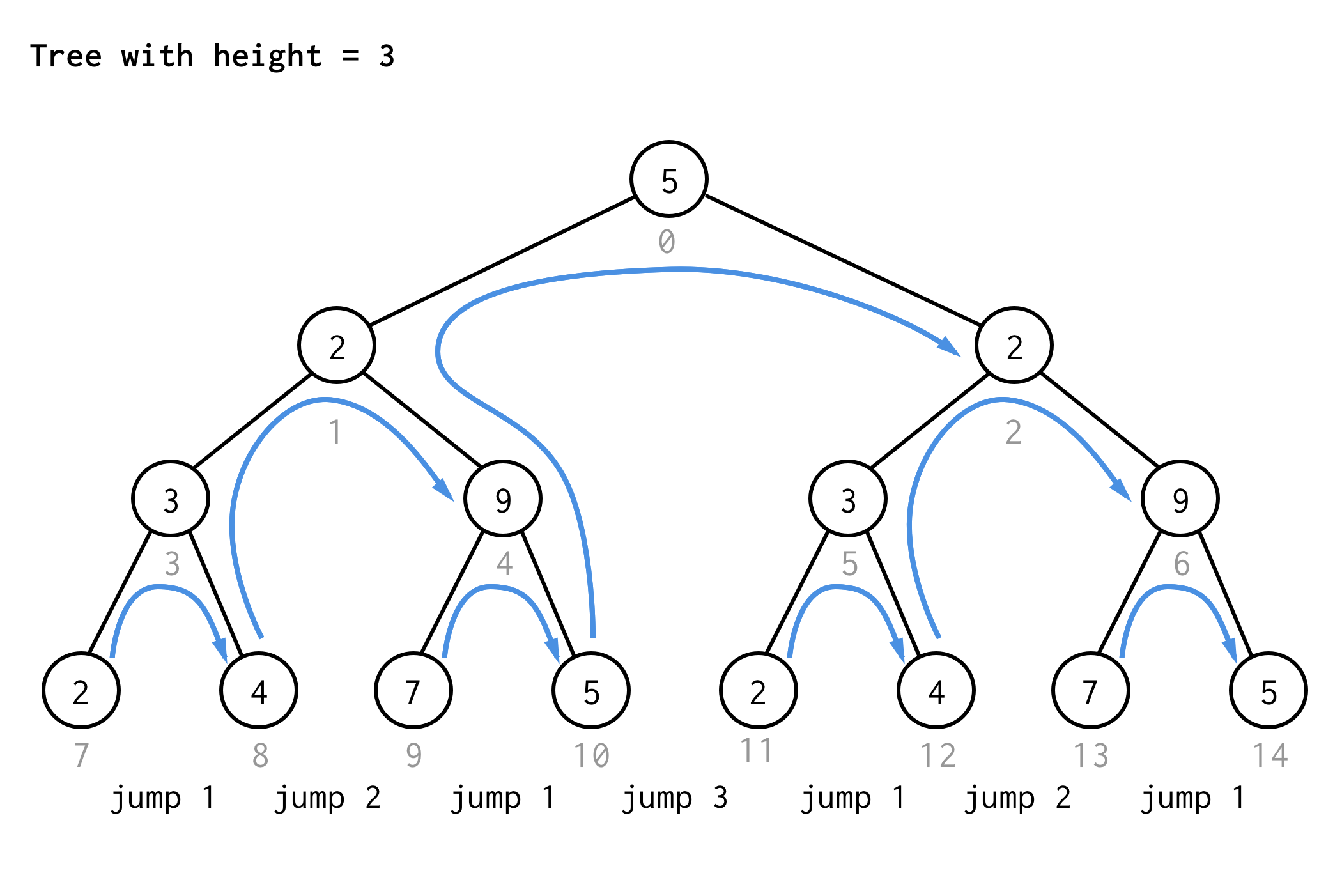
Vous voyez le modèle ?
Si vous appliquez la même règle à l’arbre de hauteur 4 et que vous n’écrivez que les valeurs des sauts, vous obtiendrez le numéro de séquence suivant
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
Cette séquence connue sous le nom de mots Zimin et elle a une définition récursive,ce qui n’est pas génial, car nous ne sommes pas autorisés à utiliser la récursion.
Trouvons une autre façon de le calculer.
Si vous regardez attentivement la séquence de saut, vous pouvez voir un modèle non récursif.
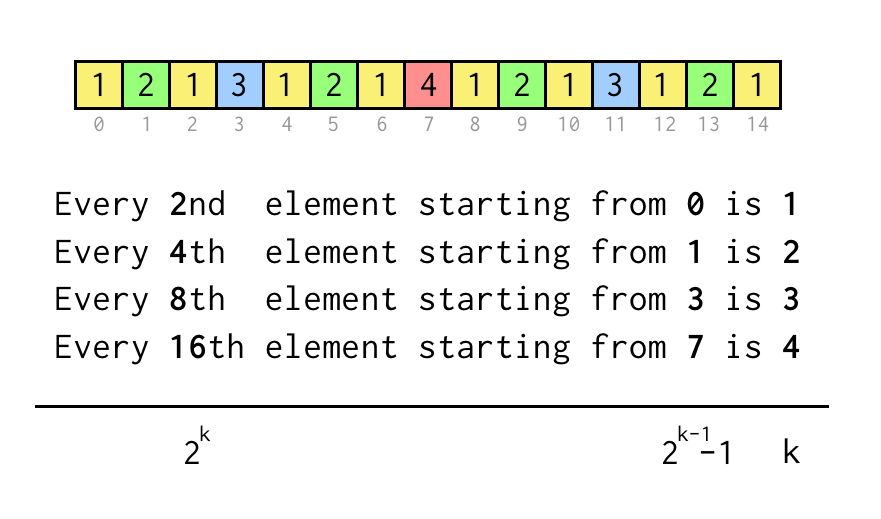
Nous pouvons suivre l’indice pour la feuille actuelle j, qui correspond à l’indice dans le tableau de la séquence ci-dessus.
Pour vérifier une déclaration comme « Chaque 8ème élément à partir de 3 » nous vérifions juste j % 8 == 3,si c’est vrai trois sauts au nœud parent requis.
Le processus de saut itératif sera le suivant
- Débuter avec
k = 1 - Sauter une fois vers le parent en appliquant
i = (i - 1)/2 - Si
leaf % 2*k == k - 1tous les sauts sont effectués, sortir - Sinon, mettre
kà2*ket répéter.
Si vous mettez tout ensemble ce que nous avons discuté
public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}Fait. DFS pour tableau d’arbre binaire sans pile et sans récursion
Complexité
La complexité semble quadratique parce que nous avons une boucle dans une boucle,mais voyons ce qu’est la réalité.
- Pour la moitié des nœuds totaux (
n/2), nous utilisons la stratégie de doublement, qui est constanteO(1) - Pour l’autre moitié des nœuds totaux (
n/2), nous utilisons la stratégie de saut de feuille. - La moitié des nœuds de saut de feuille (
n/4) nécessite un seul saut de parent, 1 itération.O(1) - La moitié de cette moitié (
n/8) nécessite deux sauts, soit 2 itérations.O(1) - …
- Seul un nœud de saut de feuille nécessite un saut complet vers la racine, qui est
O(logN) - Donc, si tous les cas ont
O(1)sauf un qui estO(logN), nous pouvons dire que la moyenne pour le saut estO(1) - La complexité totale est
O(n)
Performance
Bien que la théorie soit bonne, voyons comment cet algorithme fonctionne en pratique, en le comparant aux autres.
Nous testons 5 algorithmes, en utilisant JMH.
- BFS sur arbre binaire (liste chaînée comme file d’attente)
- BFS sur tableau d’arbre binaire (recherche linéaire)
- DFS sur arbre binaire (pile)
- DFS. sur un tableau d’arbres binaires (pile)
- DFS itératif sur un tableau d’arbres binaires
Nous avons précréé un arbre et utilisé un prédicat pour correspondre au dernier nœud,pour s’assurer que nous touchons toujours le même nombre de nœuds pour tous les algorithmes.
Donc, résultats
Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/sEvidemment, BFS sur tableau gagne. C’est juste une recherche linéaire, donc si vous pouvez représenter l’arbre binaire comme un tableau, faites-le.
La DFS itérative, que nous venons de décrire dans l’article, a pris la 2deuxième placeet 4.5 fois plus lente que la recherche linéaire (BFS sur tableau)
Les trois autres algorithmes sont encore plus lents que la DFS itérative, probablement, parce qu’ils impliquent des structures de données supplémentaires, de l’espace supplémentaire et l’allocation de mémoire.
Et le pire cas est la BFS sur arbre binaire. Je soupçonne ici la liste liée d’être un problème.
Conclusion
Le tableau d’arbre binaire est une belle astuce pour représenter une structure de données hiérarchique comme un tableau statique (région contiguë dans la mémoire). Il définit une relation d’indexation simple pour passer du parent à l’enfant, ainsi que pour passer de l’enfant au parent, ce qui n’est pas possible avec la représentation classique du tableau binaire. Quelques inconvénients, comme l’insertion/suppression lente existe, mais je suis msure qu’il y a beaucoup d’applications pour le tableau d’arbre binaire.
Comme nous l’avons montré, les algorithmes de recherche, BFS et DFS implémentés sur les tableaux sont beaucoup plus rapides que leurs frères sur une structure basée sur les références. Pour les problèmes du monde réel, ce n’est pas si important, et, probablement, je vais encore utiliser le tableau binaire basé sur la référence.
En tout cas, c’était un exercice agréable. Attendez-vous à la question « DFS sur tableau binaire sans récursion et pile » lors de votre prochain entretien.
- algorithmes
- structures de données
- programmation
mishadoff 10 septembre 2017.
Laisser un commentaire