![]()
Eigenvektorit ovat lineaariseen yhtälösysteemiin liittyvien vektoreiden erityinen joukko (i.e., matriisiyhtälöön), joita kutsutaan joskus myös ominaisvektoreiksi, ominaisvektoreiksi tai latenttivektoreiksi (Marcus ja Minc 1988, s. 144).
Systeemin ominaisvektoreiden ja ominaisarvojen määrittäminen on äärimmäisen tärkeää fysiikassa ja tekniikassa, jossa se vastaa matriisien diagonalisointia ja tulee esiin esimerkiksi sellaisissa yleisissä sovelluksissa kuin stabiilisuusanalyysi, pyörivien kappaleiden fysiikka ja värähtelevien systeemien pienet värähtelyt, vain muutamia mainitakseni. Jokaiselle ominaisvektorille on parina vastaava niin sanottu ominaisarvo. Matemaattisesti on erotettava kaksi erilaista ominaisvektorityyppiä: vasemmanpuoleiset ja oikeanpuoleiset ominaisvektorit. Monissa fysiikan ja tekniikan ongelmissa riittää kuitenkin, että tarkastellaan vain oikeita ominaisvektoreita. Tällaisissa sovelluksissa ilman tarkennusta käytetty termi ”omavektori” voidaan siis ymmärtää viittaamaan oikeaan omavektoriin.
Neliömatriisin ![]() hajottaminen ominaissuureiksi ja omavektoreiksi tunnetaan tässä työssä ominaissuureiden hajottamisena, ja se, että tämä hajottaminen on aina mahdollista, kunhan matriisin
hajottaminen ominaissuureiksi ja omavektoreiksi tunnetaan tässä työssä ominaissuureiden hajottamisena, ja se, että tämä hajottaminen on aina mahdollista, kunhan matriisin ![]() omavektoreista koostuva matriisi on neliönmuotoinen, tunnetaan ominaissuureiden hajotuslausekkeena.
omavektoreista koostuva matriisi on neliönmuotoinen, tunnetaan ominaissuureiden hajotuslausekkeena.
Määritellään oikea omavektori sarakevektoriksi ![]() , joka täyttää
, joka täyttää
|
(1)
|
jossa ![]() on matriisi, joten
on matriisi, joten
|
(2)
|
joka tarkoittaa, että oikeilla ominaissuureilla on oltava nolladeterminantti, i.e.,
|
(3)
|
Määritellään vastaavasti vasen omavektori rivivektoriksi ![]() , joka tyydyttää
, joka tyydyttää
|
(4)
|
Transponoimalla kumpikin puoli saadaan
|
(5)
|
joka voidaan kirjoittaa uudelleen muotoon
|
(6)
|
Järjestetään uudelleen, jolloin saadaan
|
(7)
|
mikä tarkoittaa
|
(8)
|
Kirjoittamalla uudelleen saadaan
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
jossa viimeinen vaihe seuraa identiteetistä
| det(A)=det(A^(T)). vasemman- ja oikeanpuoleiset ominaisarvot ovat ekvivalentteja, väite, joka ei päde ominaisvektoreille.
Olkoon
Tällöin
ja
so
Mutta tämä yhtälö on muotoa
jossa Eigenvektorit eivät saa olla yhtä suuria kuin nollavektori. Ominaisvektorin nollasta poikkeava skalaarikerrannainen vastaa alkuperäistä ominaisvektoria. Näin ollen, yleisyyden menettämättä, ominaisvektorit normalisoidaan usein yksikköpituisiksi. Vaikka Eigenvektorit voidaan laskea Wolfram-kielessä käyttämällä omavektoreita. Tämä komento palauttaa aina listan, jonka pituus on Annetaan
Sovelletaan matriisia
so
Jos
siten matriisin toistuva soveltaminen mielivaltaiseen vektoriin hämmästyttävällä tavalla johtaa ina vektoriin, joka on verrannollinen suurimman ominaisarvon omaavaan ominaisvektoriin. |
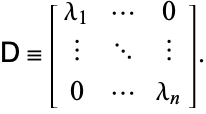
Vastaa