mishadoffin ajatuksia

Syvyys-ensimmäisen haun toteuttaminen binääripuulle ilman pinoa ja rekursiota.

Binääripuujoukko

Tämä on binääripuu.

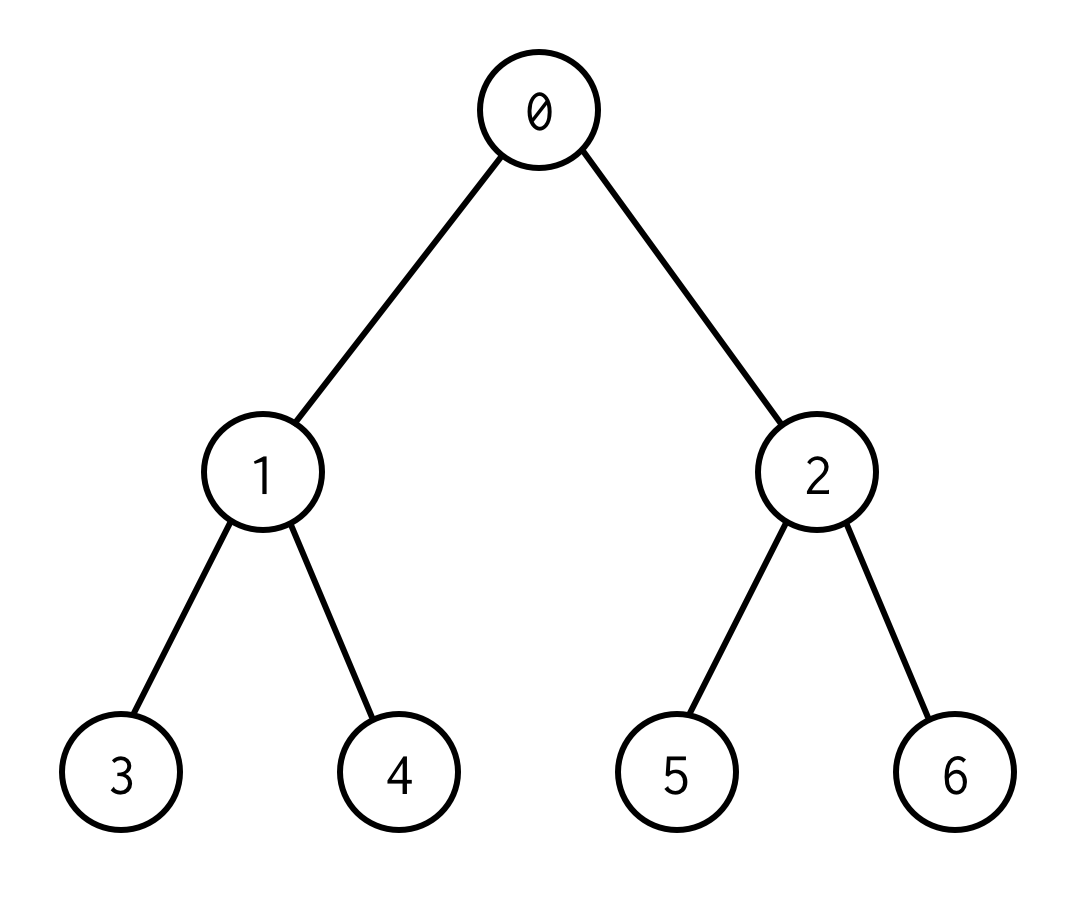
0 on juurisolmu.
0:lla on kaksi lasta: vasen 1 ja oikea: 2.
Kullakin sen lapsella on lapsensa ja niin edelleen.
Solmut, joilla ei ole lapsia, ovat lehtisolmuja (3,4,5,6).

Juuri- ja lehtisolmujen välisten särmien määrä määrittelee puun korkeuden.yllä olevan puun korkeus on 2.

Tavanomainen tapa toteuttaa binääripuu on määritellä luokka nimeltä BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Mutta on olemassa kikka, jolla binääripuu voidaan toteuttaa käyttämällä vain staattisia matriiseja.Jos luetellaan kaikki binääripuun solmut tasoittain nollasta alkaen, voidaan ne pakata matriisiin.

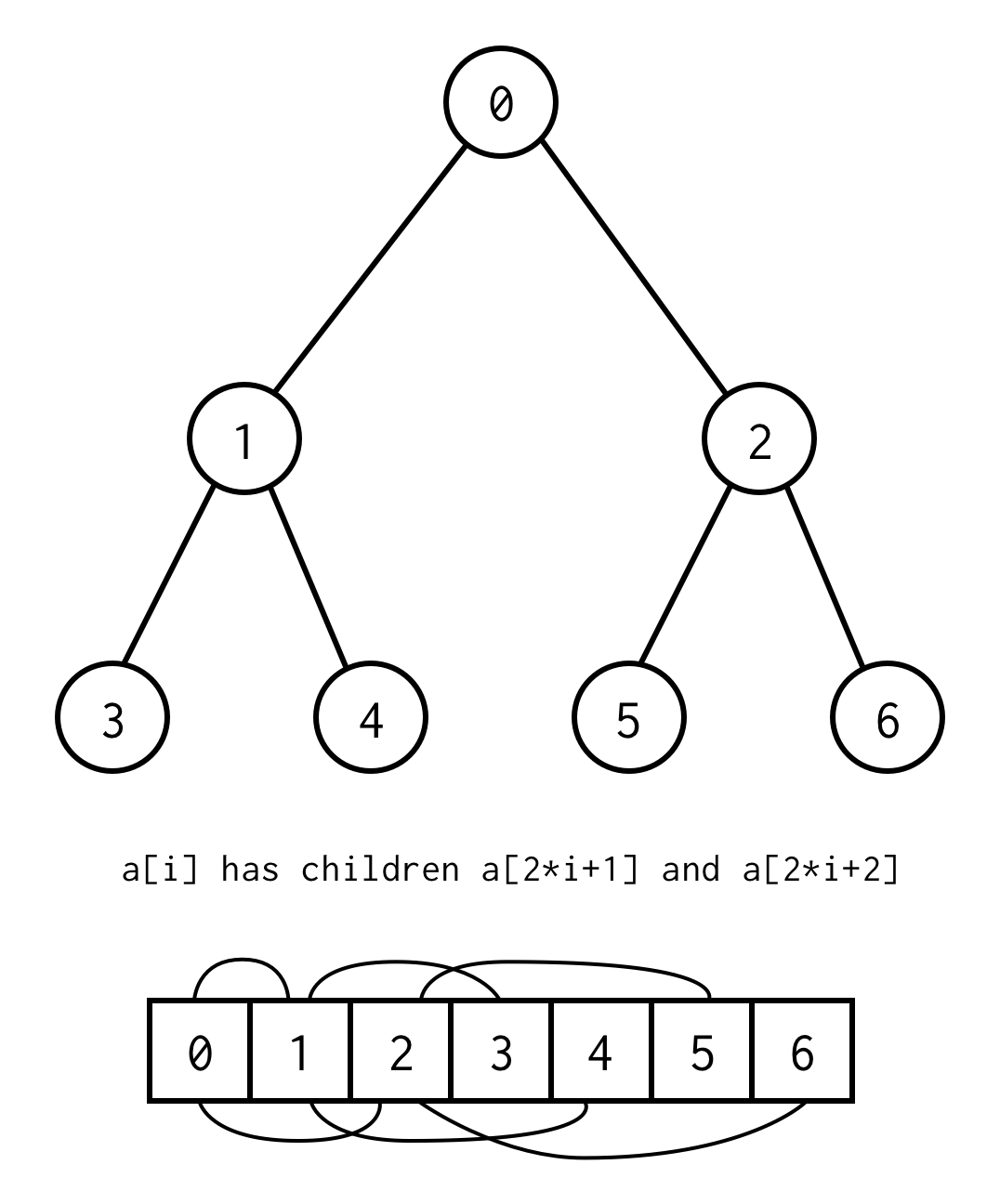
Vanhemman indeksin ja lapsen indeksin välinen suhde,mahdollistaa siirtymisen vanhemmasta lapseen sekä lapsesta vanhempaan

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Tärkeää on huomioida, että puun tulee olla täydellinen, mikä tarkoittaa, että tietyllä korkeudella sen tulee sisältää täsmälleen elementtejä.

Voit välttää tällaisen vaatimuksen sijoittamalla null puuttuvien elementtien tilalle.

Luettelu koskee edelleen myös tyhjiä solmuja. Tämän pitäisi kattaa kaikki mahdolliset binääripuut.

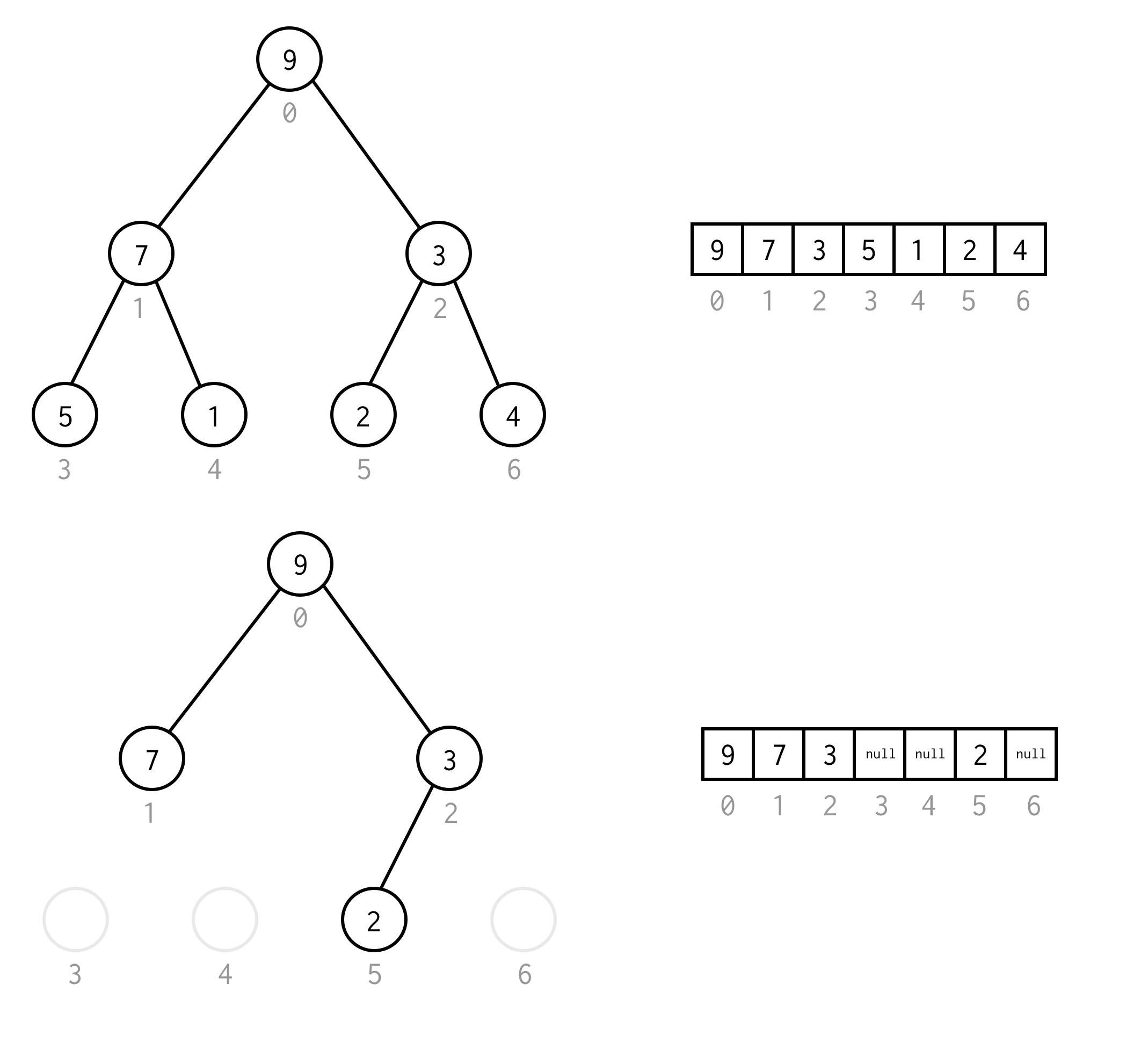
Tällaista array-esitystä binääripuulle kutsumme Binary Tree Array:ksi.Oletamme aina, että se sisältää elementtejä.

BFS vs. DFS

Binääripuulle on olemassa kaksi hakualgoritmia:leveyshaku (breadth-first search, BFS) ja syvyyshaku (depth-first search, DFS).

Parhaimmin ymmärrämme ne visuaalisesti

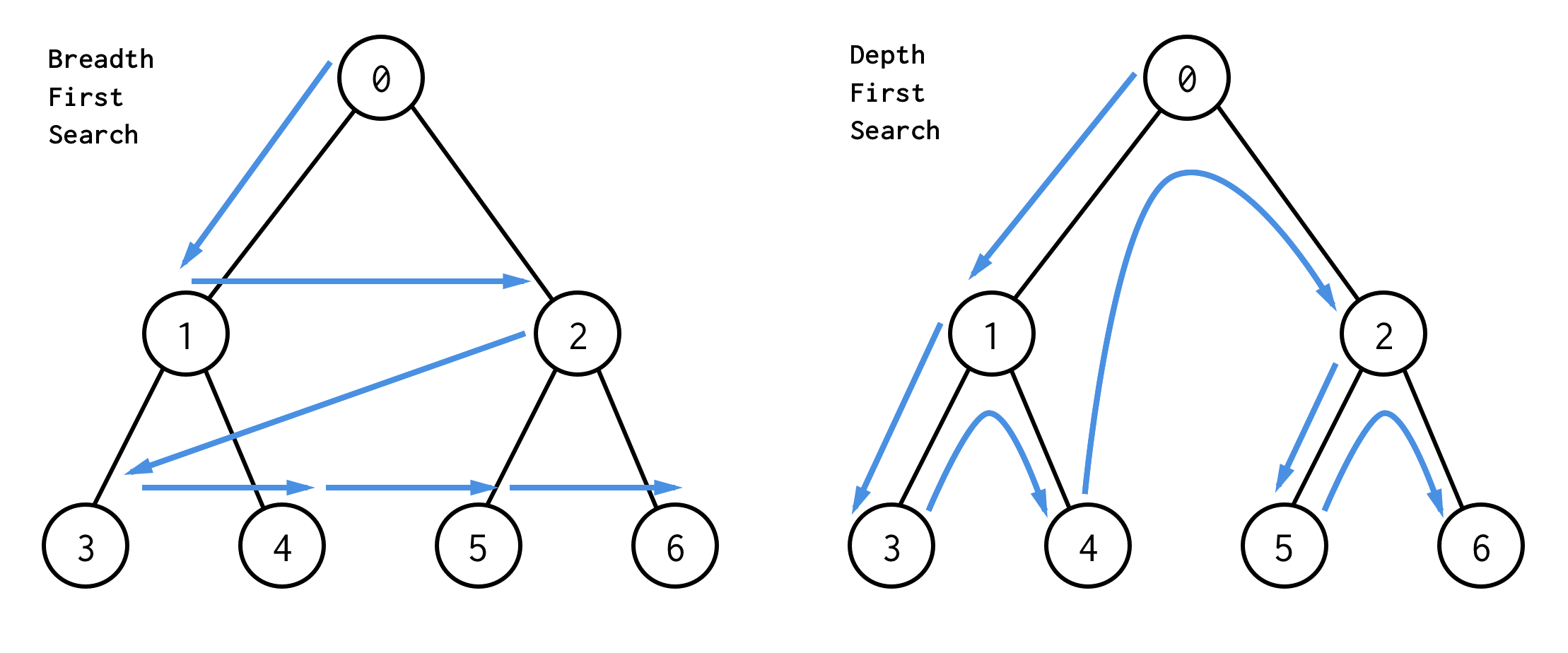
BFS:llä etsitään solmuja taso kerrallaan aloittaen juurisolmusta. Sitten tarkistetaan sen lapset. Kunnes kaikki solmut on käsitelty tai hakuehdon täyttävä solmu on löydetty.

DFS käyttäytyy eri tavalla. Se tarkistaa kaikki solmut vasemmanpuoleisimmasta polusta juuresta lehteen,sitten hyppää ylöspäin ja tarkistaa oikeanpuoleisen solmun jne.

Klassisten binääripuiden osalta BFS on toteutettu käyttämällä Queue-tietorakennetta (LinkedList implements Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Jos korvataan jono pinoilla, saadaan DFS-toteutus.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Esimerkiksi oletetaan, että seuraavasta puusta pitää löytää solmu, jonka arvo on 1.

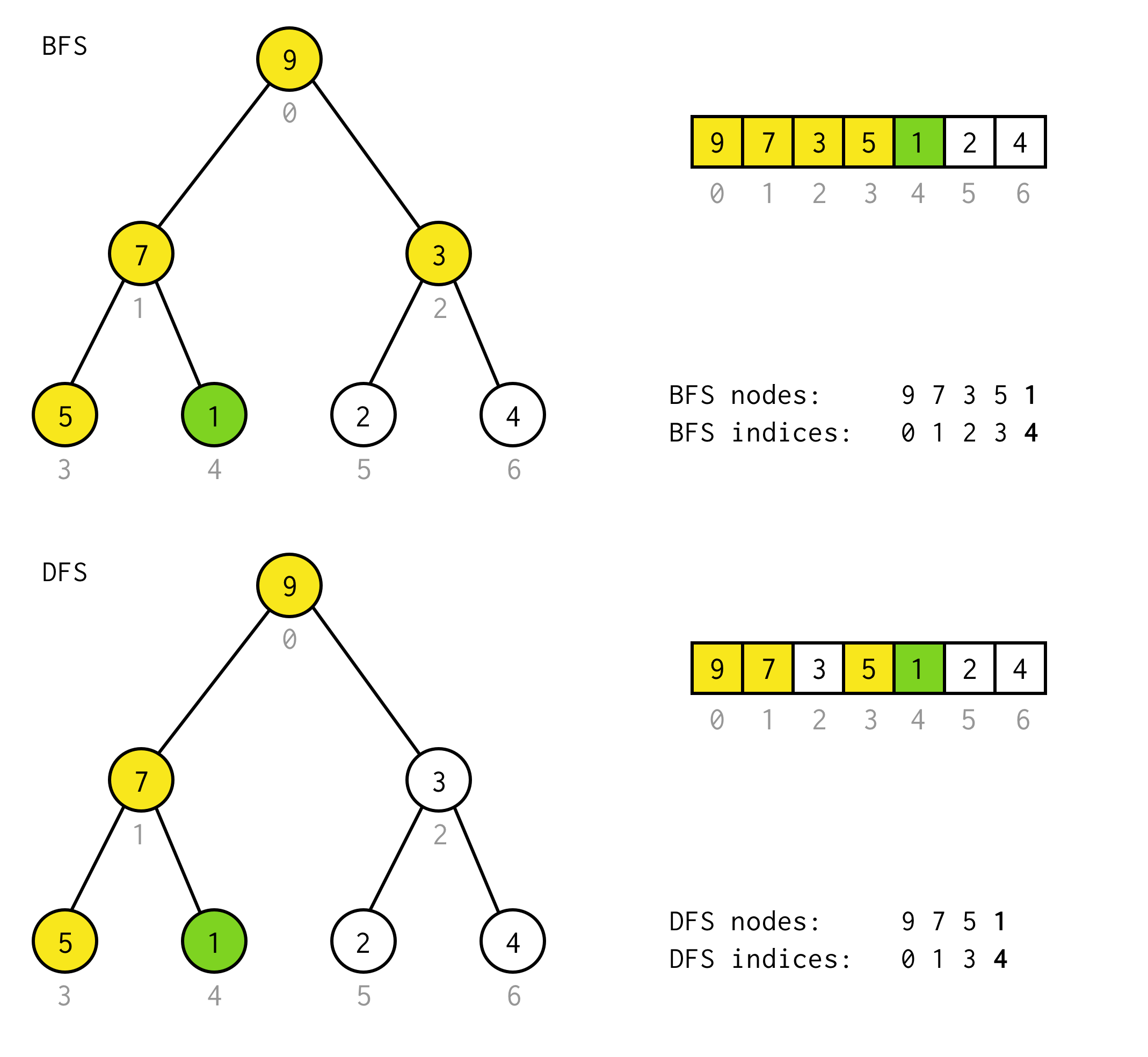
Keltaiset solut ovat soluja, jotka testataan hakualgoritmissa, ennen kuin tarvittava solmu löydetään.Ota huomioon, että joissakin tapauksissa DFS vaatii vähemmän solmuja käsittelyyn.

Pinon tietorakennetta käyttäen se voitaisiin toteuttaa samalla tavalla kuin klassiselle binääripuulle,laitetaan vain indeksit pinoon.

Tältä osin rekursio ei eroa lainkaan,käytetään vain implisiittistä metodikutsupinoa tietorakenteen pinon sijasta.

Mitä jos voisimme toteuttaa DFS:n ilman pinoa ja rekursiota.Loppujen lopuksi on vain oikean indeksin valitseminen jokaisella askeleella?

Kokeillaan.

DFS for Binary Tree Array (ilman pinoa ja rekursiota)

Kuten BFS:ssä aloitamme juuri-indeksistä 0.
Sitten meidän täytyy tarkastaa sen vasen lapsi, jonka indeksi voitaisiin laskea kaavalla 2*i+1.
Kutsutaan prosessia, jossa mennään seuraavaan vasempaan lapseen kaksinkertaistamalla.

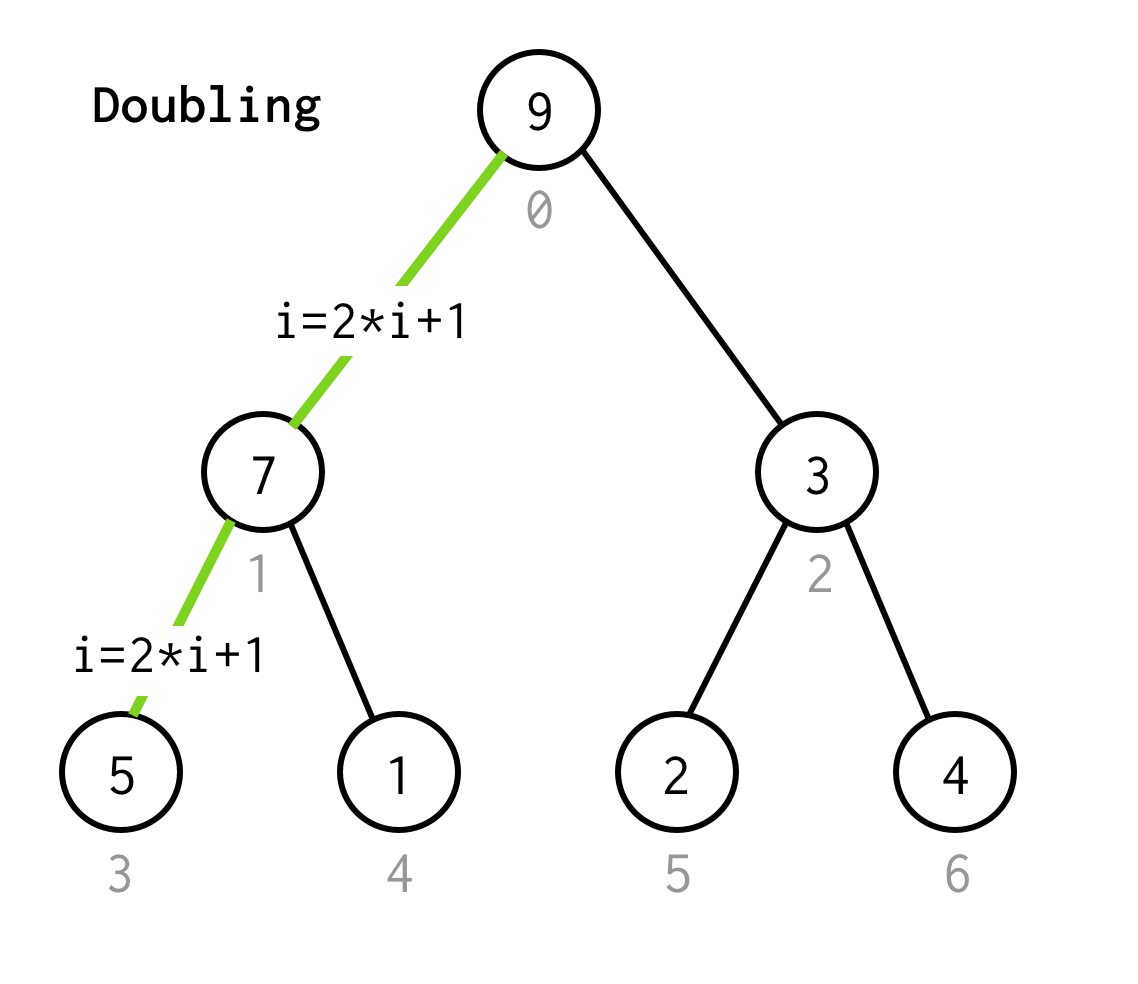
Jatkamme indeksin kaksinkertaistamista kunnes emme pysähdy lehtisolmuun.

Miten siis ymmärrämme, että kyseessä on lehtisolmu?

Jos seuraava vasen lapsi tuottaa indeksin out of array bounds -poikkeuksen, meidän on lopetettava kaksinkertaistaminen ja hypättävä oikeaan lapseen.

Tämä on kelvollinen ratkaisu, mutta voimme välttää tarpeettoman kaksinkertaistamisen.Havainto tässä on se, että elementtien määrä puussa jollain height on kaksi kertaa suurempi (ja plus yksi)kuin puussa jossa on height - 1.

Puussa, jossa on height = 2, on 7 elementtiä, puussa, jossa on height = 3, on 7*2+1 = 15 elementtiä.

Tämän havainnon avulla muodostamme yksinkertaisen ehdon

i < array.length / 2

Voidaan tarkistaa, että tämä ehto pätee mille tahansa puun ei-lehti-solmulle.

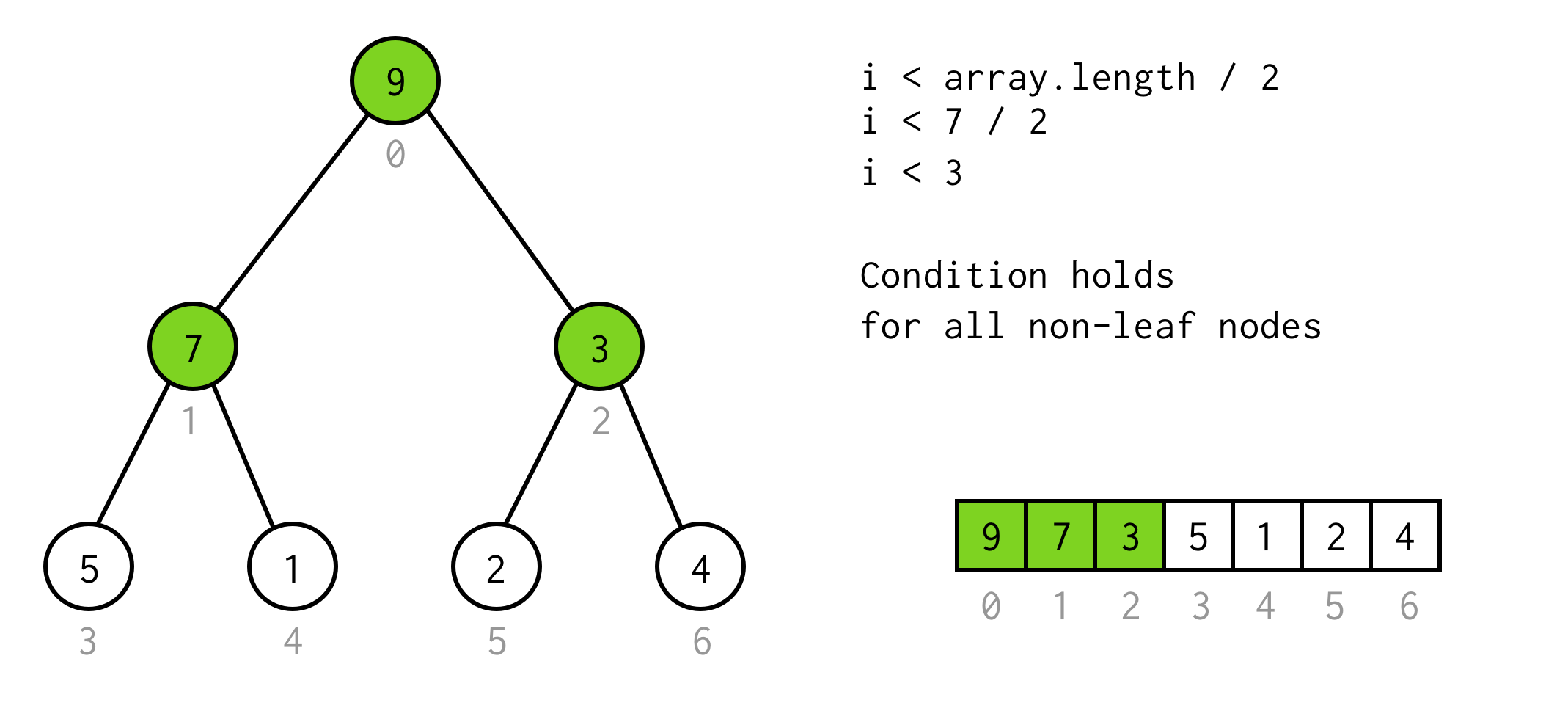
Kiva tähän asti. Voimme suorittaa kaksinkertaistamisen, ja tiedämme jopa, milloin se on lopetettava. mutta tällä tavalla voimme tarkistaa vain solmujen vasemmanpuoleiset lapset.

Kun olemme juuttuneet lehtisolmuun emmekä voi enää soveltaa kaksinkertaistamista, suoritamme hyppyoperaation.Periaatteessa, jos kaksinkertaistaminen on mennä vasempaan lapseen, hyppy on mennä vanhempaan ja mennä oikeaan lapseen.

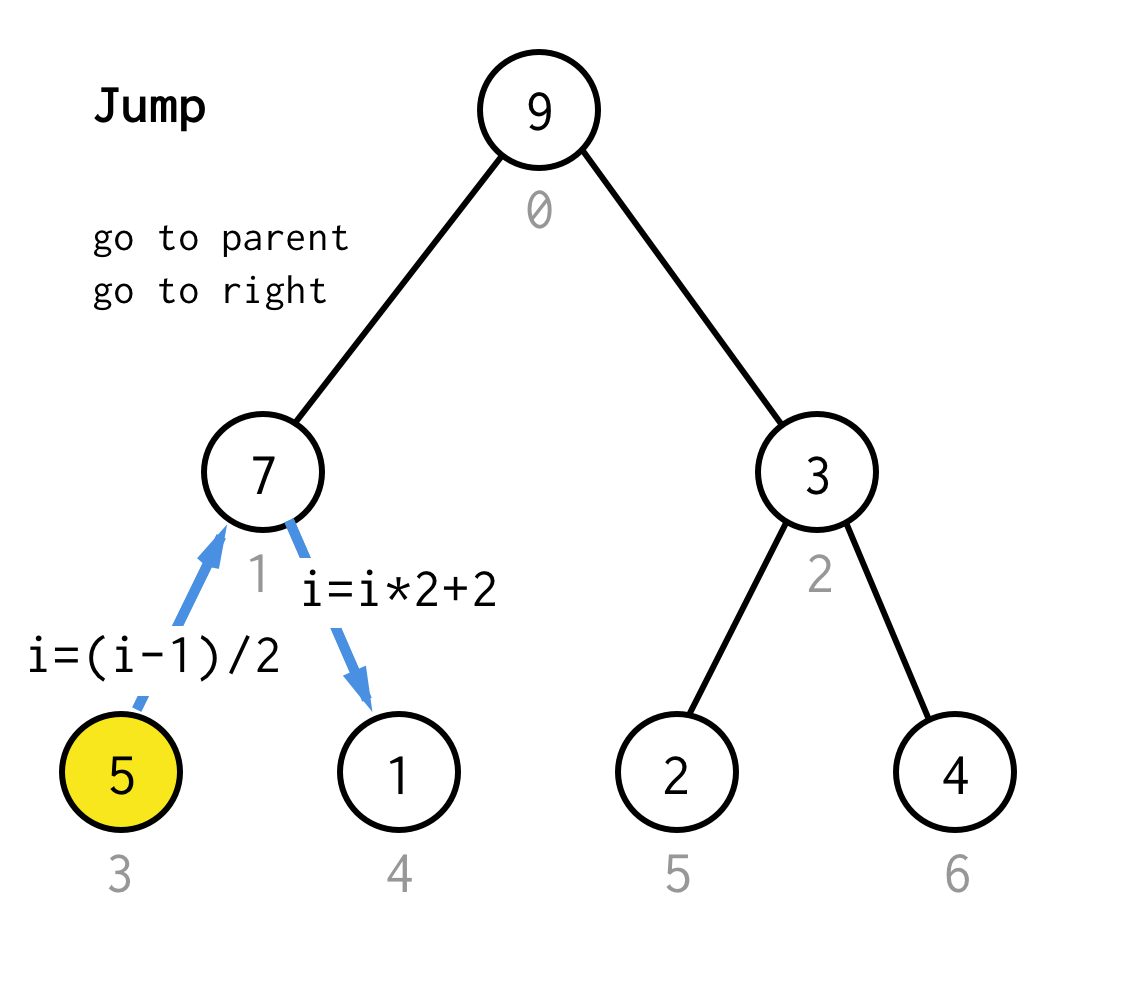
Tällainen hyppyoperaatio voidaan toteuttaa vain inkrementoimalla lehti-indeksiä.Mutta kun olemme juuttuneet seuraavaan lehtisolmuun, inkrementoiminen ei siirrä solmua seuraavaan solmuun, mikä vaaditaan DFS:ssä.Joten meidän on tehtävä kaksinkertainen hyppy

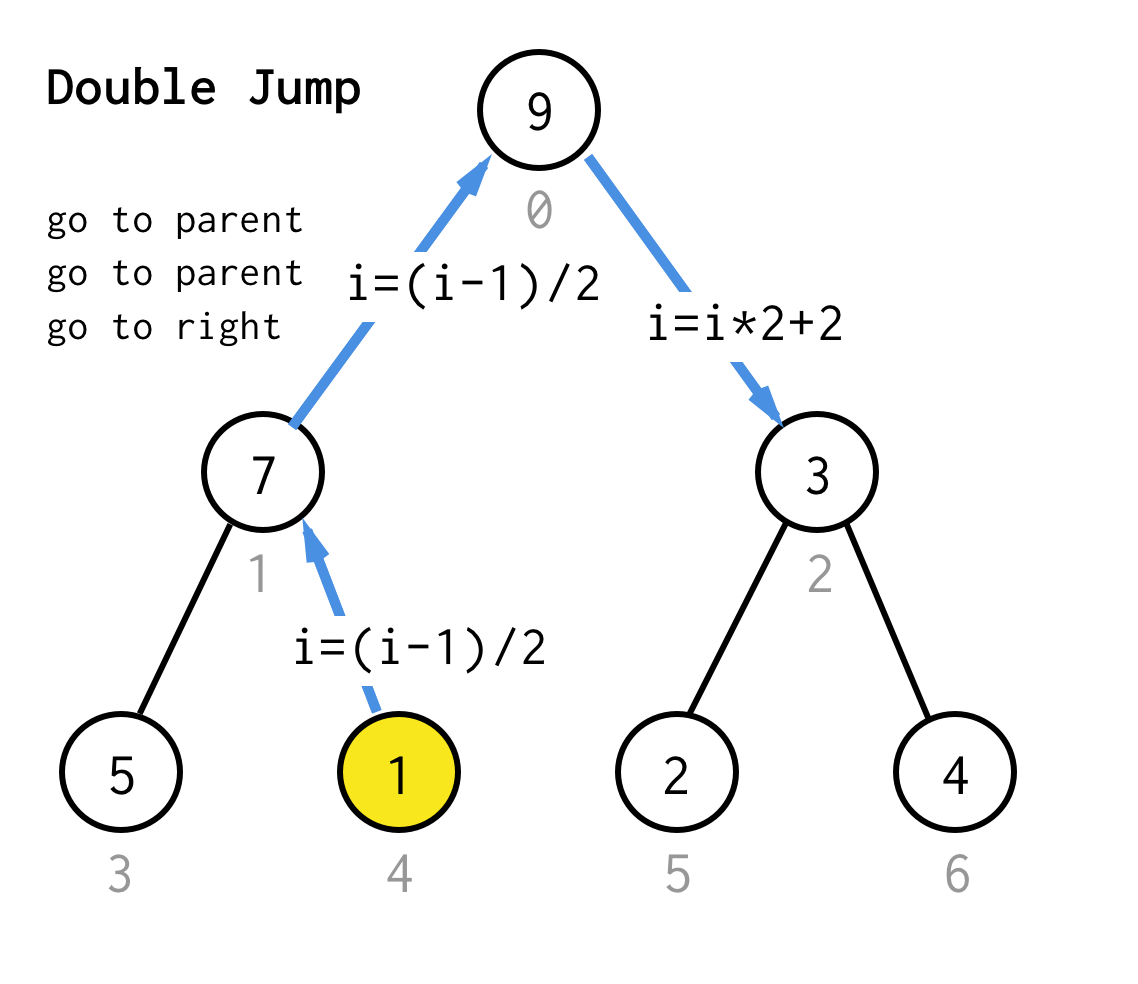
Tehdäksemme siitä geneerisemmän, algoritmillemme voisimme määritellä operaation hyppy N, joka määrittelee, kuinka monta hyppyä vanhempaan se vaatii ja päättyy aina yhteen hyppyyn oikeaan lapseen.

Puulle, jonka korkeus on 1, tarvitaan yksi hyppy, hyppy 1

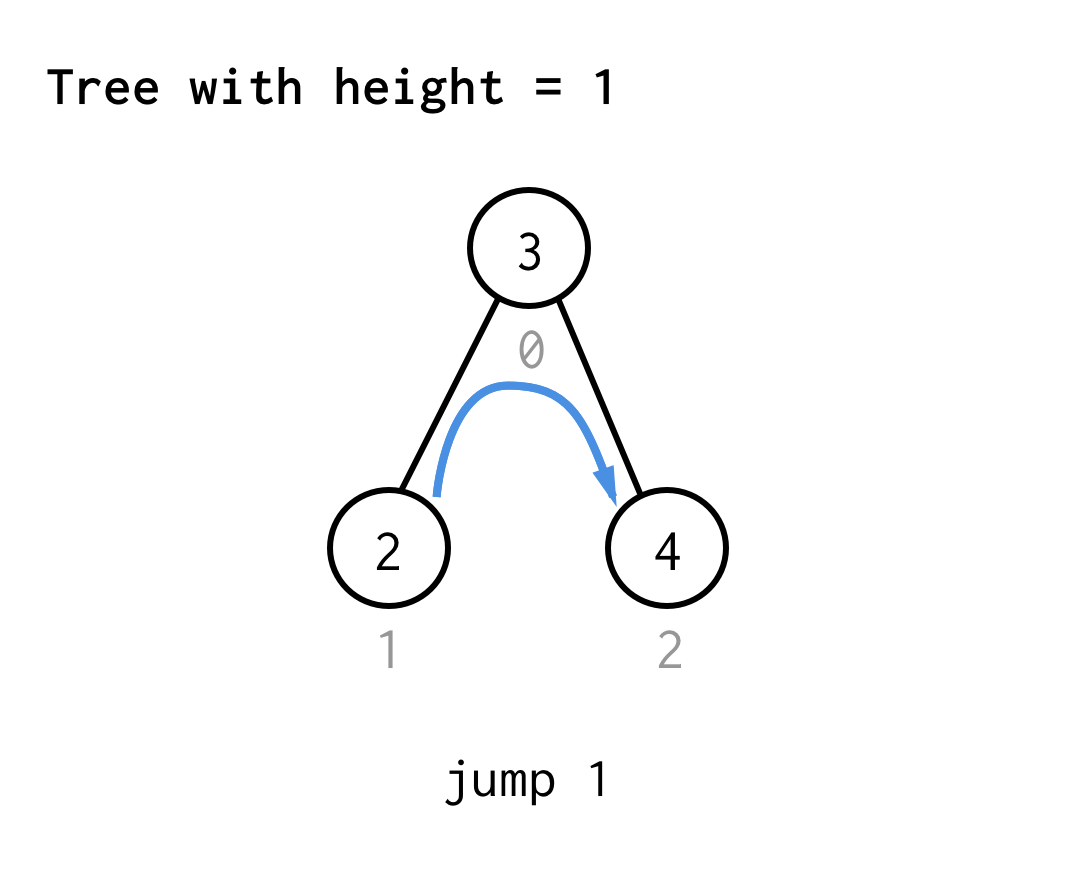
Puulle, jonka korkeus on 2, tarvitaan yksi hyppy, yksi tuplahyppy ja sitten taas yksi hyppy

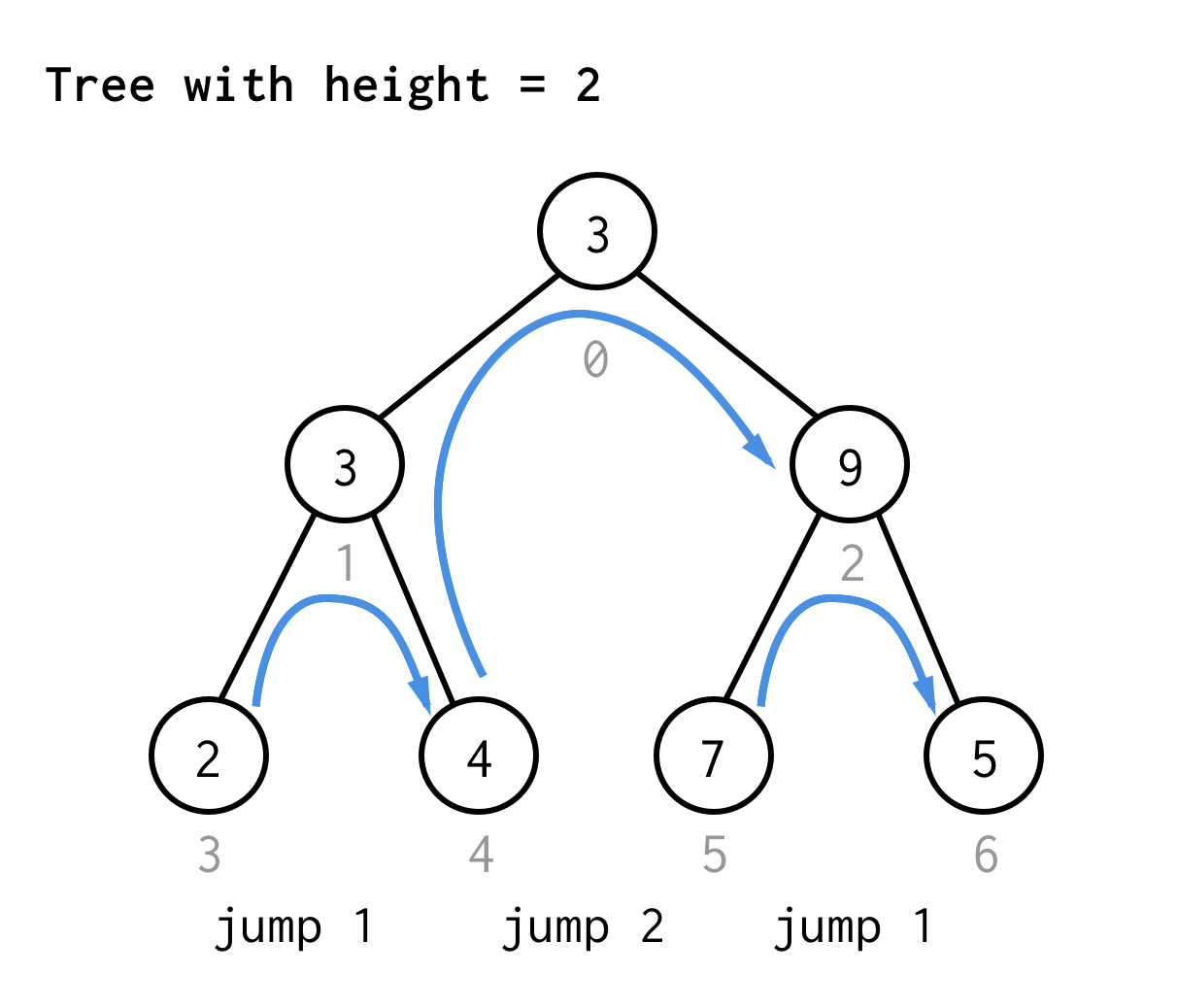
Puuseen, jonka korkeus on 3, voidaan soveltaa samoja sääntöjä ja saada 7 hyppyä.

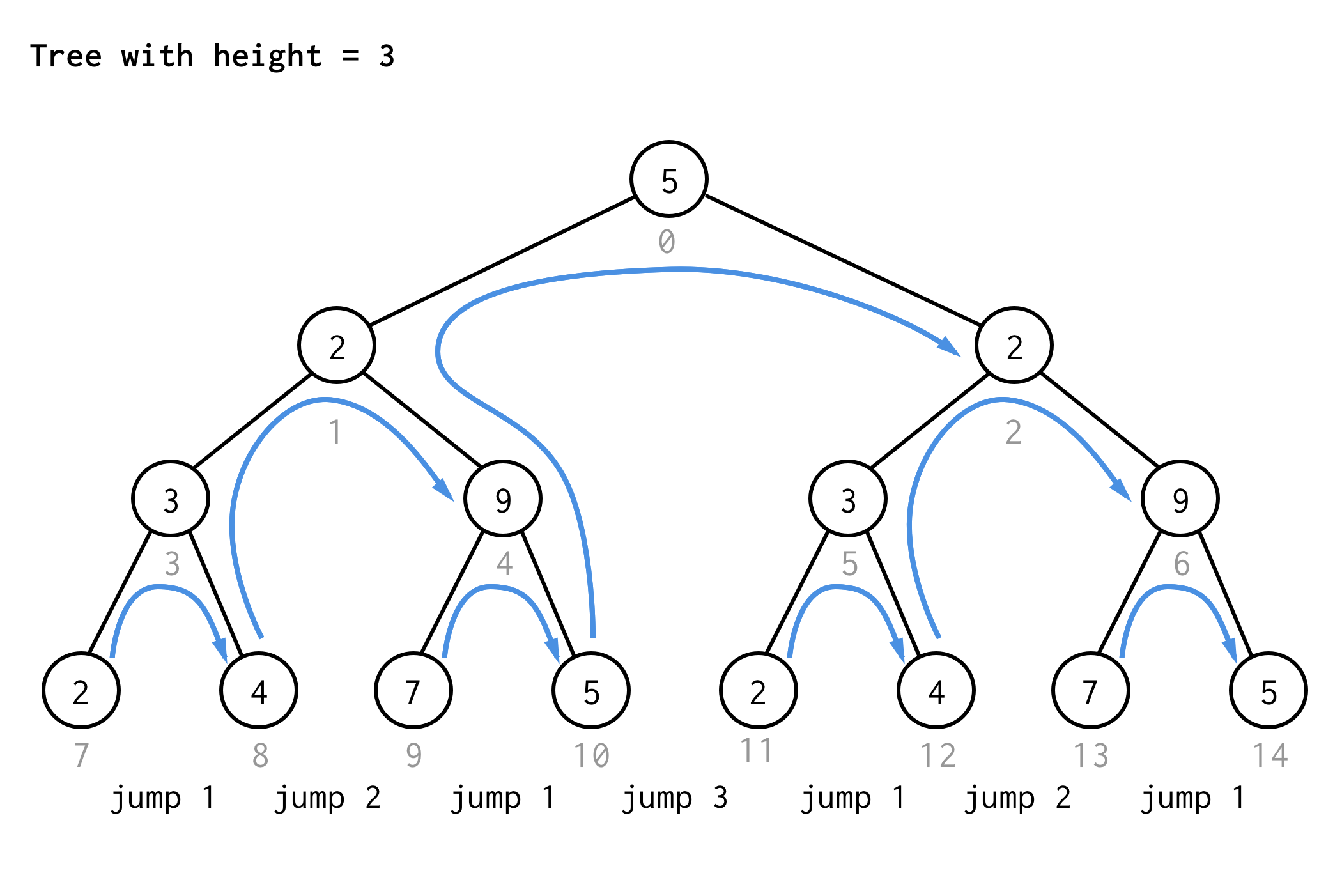
Näkyykö kuvio?

Jos sovellat samaa sääntöä puuhun, jonka korkeus on 4 ja kirjoitat ylös vain hyppyarvot, saat seuraavan järjestysluvun

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Tämä järjestys tunnetaan nimellä Zimin-sanat ja sillä on rekursiivinen määritelmä,joka ei ole hyvä, koska emme saa käyttää rekursiota.

Keksitään jokin toinen tapa laskea se.

Jos katsot tarkkaan hyppysekvenssiä, näet ei-rekursiivisen kuvion.

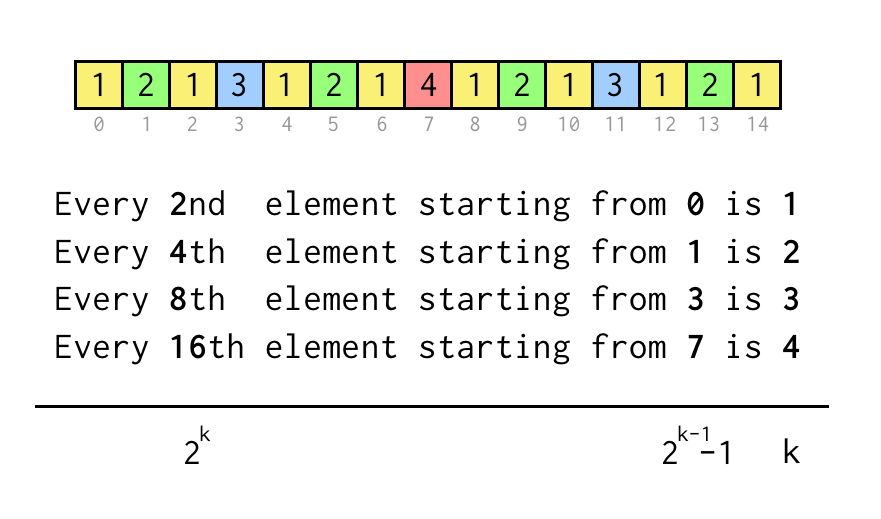
Voidaan seurata nykyisen lehden j indeksiä, joka vastaa indeksiä yllä olevassa sekvenssirakenteessa.

Varmistaaksemme väitteen kuten ”Every 8th element starting from 3” tarkistamme vain j % 8 == 3,jos se on totta kolme hyppyä vanhemman solmun vaatimaan solmuun.

Iteratiivinen hyppyprosessi on seuraava

• Aloitetaan k = 1
• Hyppää kerran vanhempaan solmuun soveltamalla i = (i - 1)/2
• Jos leaf % 2*k == k - 1 kaikki hypyt suoritettu, poistutaan
• Muussa tapauksessa asetetaan k arvoksi 2*k ja toistetaan.

Jos laitat kaikki yhteen, mitä olemme keskustelleet

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Tehdään. DFS binary tree arraylle ilman pinoa ja rekursiota

Kompleksisuus

Kompleksisuus näyttää kvadraattiselta koska meillä on silmukka silmukassa,mutta katsotaanpa mikä on todellisuus.

• Puolelle kaikista solmuista (n/2) käytämme kaksinkertaistamisstrategiaa, joka on vakio O(1)
• Toiselle puolelle kaikista solmuista (n/2) käytämme lehtihyppystrategiaa.
• Puolet lehtihyppysolmuista (n/4) vaativat vain yhden vanhemman hyppytoiminnon, 1 iteraation. O(1)
• Puoli tästä puolesta (n/8) vaatii kaksi hyppyä eli 2 iteraatiota. O(1)
• …
• Vain yksi lehtihyppysolmu vaatii täyden hypyn juureen, joka on O(logN)
• Jos siis kaikissa tapauksissa on O(1) paitsi yhdessä, joka on O(logN), voimme sanoa, että hyppyjen keskiarvo on O(1)
• Kokonaiskompleksisuus on O(n)

Suorituskyky

Vaikka teoria on hyvä, katsotaanpa, miten tämä algoritmi toimii käytännössä verrattuna muihin.

Testaamme 5 algoritmia käyttäen JMH:ta.

• BFS binääripuulla (linkitetty lista jonona)
• BFS binääripuulla Array (lineaarinen haku)
• DFS binääripuulla (pino)
• DFS. on Binary Tree Array (stack)
• Iterative DFS on Binary Tree Array

Olemme luoneet puun valmiiksi ja käyttäneet predikaattia viimeisen solmun löytämiseen,varmistaaksemme, että osumme aina samaan määrään solmuja kaikissa algoritmeissa.

Tulokset

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Ilmeisesti BFS on array voittaa. Se on vain lineaarinen haku, joten jos voit esittää binääripuun arraynä, tee se.

Iteratiivinen DFS, jonka juuri kuvailimme artikkelissa, otti 2toisen sijan ja oli 4.5 kertaa hitaampi kuin lineaarinen haku (BFS on array)

Kolme muuta algoritmia vielä hitaampia kuin iteratiivinen DFS, luultavasti siksi, että niihin liittyylisättömiä tietorakenteita, ylimääräistä tilaa ja muistin allokointia.

Pahin tapaus on BFS binääripuuhun. Epäilen, että tässä linkitetty lista on ongelma.

Johtopäätös

Binary Tree Array on kiva temppu esittää hierarkkinen tietorakenne staattisena arraynä (yhtenäinen alue muistissa). Se määrittelee yksinkertaisen indeksisuhteen siirryttäessä vanhemmalta lapselle sekä siirryttäessä lapselta vanhemmalle, mikä ei ole mahdollista klassisella binäärimassojen esitystavalla. Joitakin haittoja, kuten hidas lisääminen/poistaminen, on olemassa, mutta olen varma, että binääripuumassoille on paljon sovelluksia.

Kuten olemme osoittaneet, hakualgoritmit, BFS ja DFS, jotka on toteutettu matriiseilla, ovat paljon nopeampia kuin niiden veljet referenssipohjaisella rakenteella. Reaalimaailman ongelmissa se ei ole niin tärkeää, ja luultavasti käytän edelleen referenssipohjaista binäärimassaa.

Jokatapauksessa tämä oli mukava harjoitus. Odota kysymystä ”DFS on binary array without recursion and stack” seuraavassa haastattelussasi.

• algorithms
• datastructures
• programming

mishadoff 10. syyskuuta 2017