Propiedades de los ángulos de un triángulo

Temas relacionados:
Más lecciones de geometría
Hojas de trabajo de geometría
Juegos de geometría
En estas lecciones, daremos un resumen de las propiedades de los ángulos de un triángulo.

• Teorema de la suma de triángulos – La suma de los 3 ángulos de un triángulo es siempre 180°
• La suma de un ángulo interior y su ángulo exterior adyacente es 180°
• Teorema del ángulo exterior – Un ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores opuestos
• Un triángulo equilátero tiene 3 ángulos iguales de 60° cada uno. Un triángulo isósceles tiene 2 ángulos iguales, que son los ángulos opuestos a los 2 lados iguales

Los ángulos de un triángulo tienen las siguientes propiedades:

Propiedad 1: Teorema de la suma de triángulos

La suma de los 3 ángulos de un triángulo es siempre 180°.

Ejemplo :

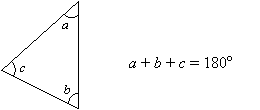
¿Cómo demostrar el Teorema de la suma de triángulos?
El siguiente vídeo muestra cómo demostrar que la suma de los ángulos de un triángulo es 180 grados. (Teorema de la suma de triángulos)

• Mostrar soluciones paso a paso

¿Cómo encontrar el ángulo que falta en un triángulo utilizando el teorema de la suma de triángulos?
Paso 1: Escribir la ecuación sumando todos los ángulos y haciéndolos iguales a 180°.
Paso 2: Resolver para x.
Paso 3: Sustituir para encontrar los ángulos que faltan.

• Mostrar soluciones paso a paso

Propiedad 2:

La suma de un ángulo interior y su ángulo exterior adyacente es 180°.

Ejemplo :

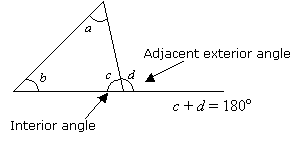
Propiedad 3: Teorema del ángulo exterior

Un ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores opuestos.

Ejemplo :

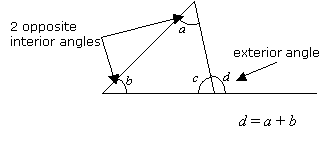
Ángulos exteriores de un triángulo
Hallar el ángulo desconocido de un triángulo
Ejemplo:
1. Evaluar el triángulo abc, donde a = 40° y b = 60°. ¿Cuál es el ángulo exterior a ∠acb?
2. Evalúa el triángulo abc, donde a = 50° y b = 30°. ¿Cuál es el ángulo exterior a ∠acb?
2. Evalúa el triángulo abc, donde a = 90° y b = 40°. Cuál es el ángulo exterior a ∠acb?

• Mostrar soluciones paso a paso

¿Cómo utilizar el teorema del ángulo exterior para resolver problemas que implican ángulos en un triángulo?

• Mostrar soluciones paso a paso

Propiedad 4:

Un triángulo equilátero tiene 3 ángulos iguales de 60° cada uno.
Un triángulo isósceles tiene 2 ángulos iguales, que son los ángulos opuestos a los 2 lados iguales.
¿Cómo encontrar el ángulo que falta en un triángulo isósceles?

• Mostrar soluciones paso a paso

Las líneas paralelas y el teorema de la suma de los ángulos de los triángulos

• Mostrar soluciones paso a paso

Las propiedades de los ángulos anteriores pueden ayudarnos a encontrar ángulos desconocidos en un triángulo.

Ejemplo:

Encuentra el valor de x en el siguiente triángulo.

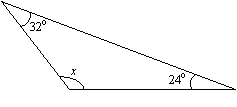
Solución:

x + 24° + 32° = 180° (la suma de los ángulos es 180°)
x + 56° = 180°
x = 180° – 56° = 124°

Ejemplo :

Encuentra los valores de x e y en el siguiente triángulo.

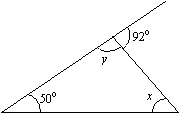
Solución:

x + 50° = 92° (suma de ángulos interiores opuestos = ángulo exterior)
x = 92° – 50° = 42°

y + 92° = 180° (ángulo interior + ángulo exterior adyacente = 180°.)
y = 180° – 92° = 88°

Prueba la calculadora y el solucionador de problemas gratuitos de Mathway que aparecen a continuación para practicar varios temas de matemáticas. Prueba los ejemplos dados, o escribe tu propio problema y comprueba tu respuesta con las explicaciones paso a paso.