pensamientos de Mishadoff

Implementación de la Búsqueda en Profundidad para el Árbol Binario sin pila y recursión.

Array de Árboles Binarios

Esto es un árbol binario.

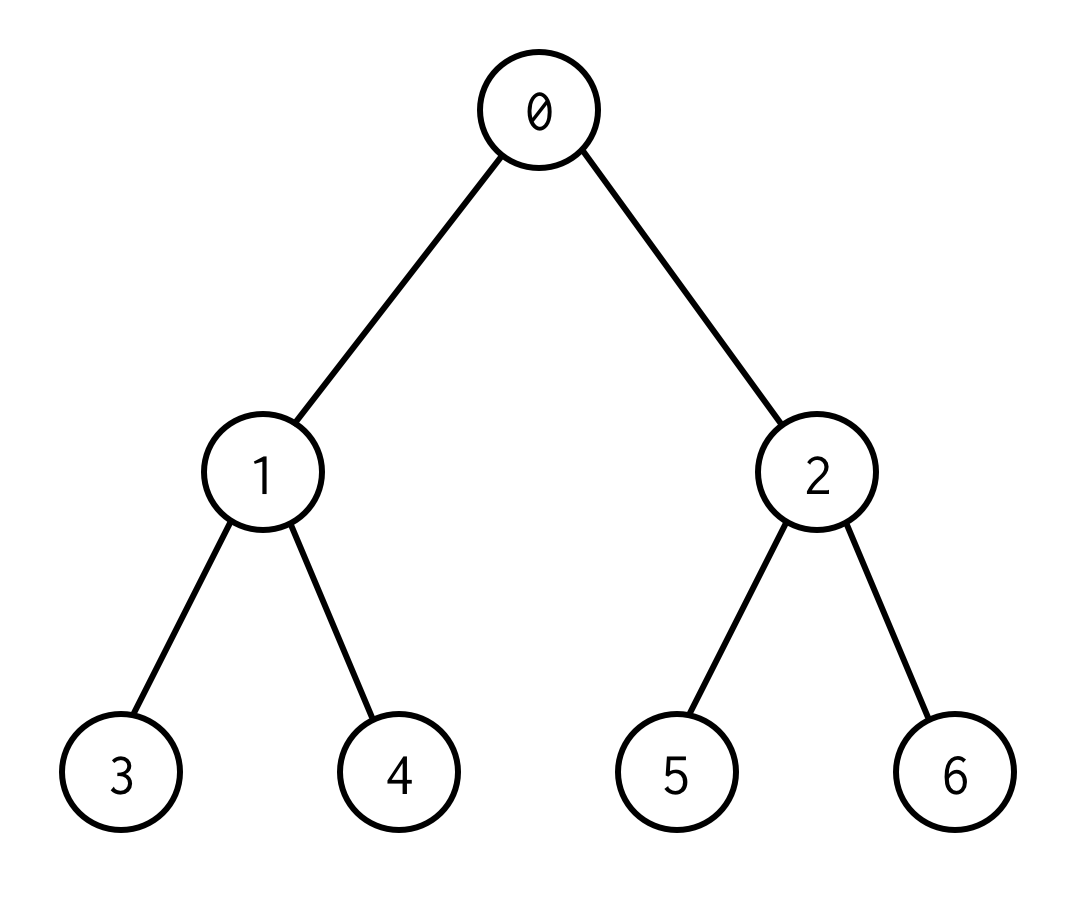
0es un nodo raíz.
0tiene dos hijos: izquierdo 1 y derecho: 2.
Cada uno de sus hijos tiene sus hijos y así sucesivamente.
Los nodos sin hijos son nodos hoja (3,4,5,6).

El número de aristas entre los nodos raíz y hoja definen la altura del árbol.El árbol de arriba tiene la altura 2.

El método estándar para implementar el árbol binario es definir una clase llamada BinaryNode

public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}

Sin embargo, hay un truco para implementar el árbol binario utilizando sólo arrays estáticos.

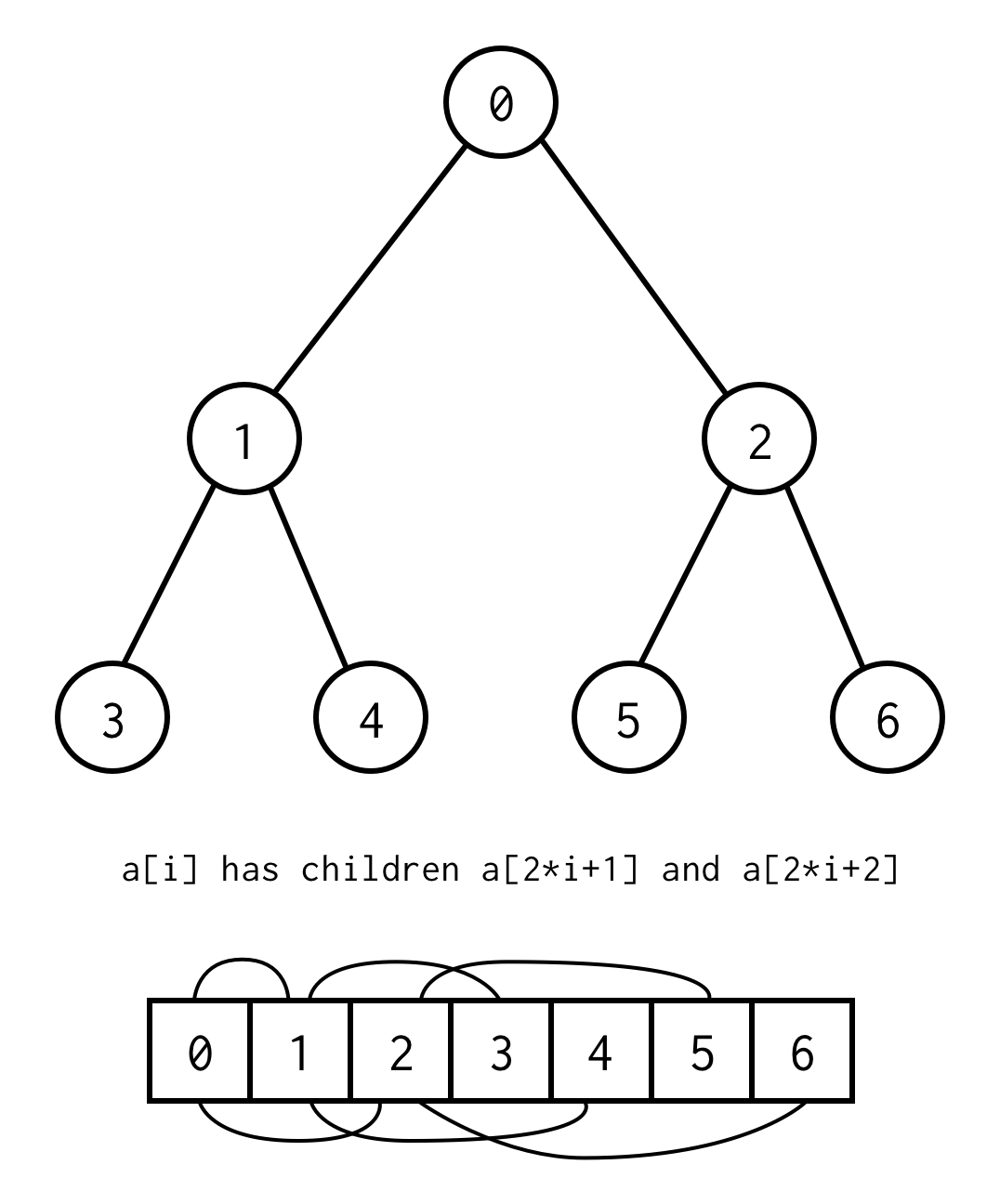
La relación entre el índice padre y el índice hijo, nos permite movernos del padre al hijo, así como del hijo al padre

left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2

Nótese que el árbol debe ser completo, lo que significa que para la altura específica debe contener exactamente elementos.

Se puede evitar este requisito colocando null en lugar de los elementos que faltan. Esto debería cubrir cualquier árbol binario posible.

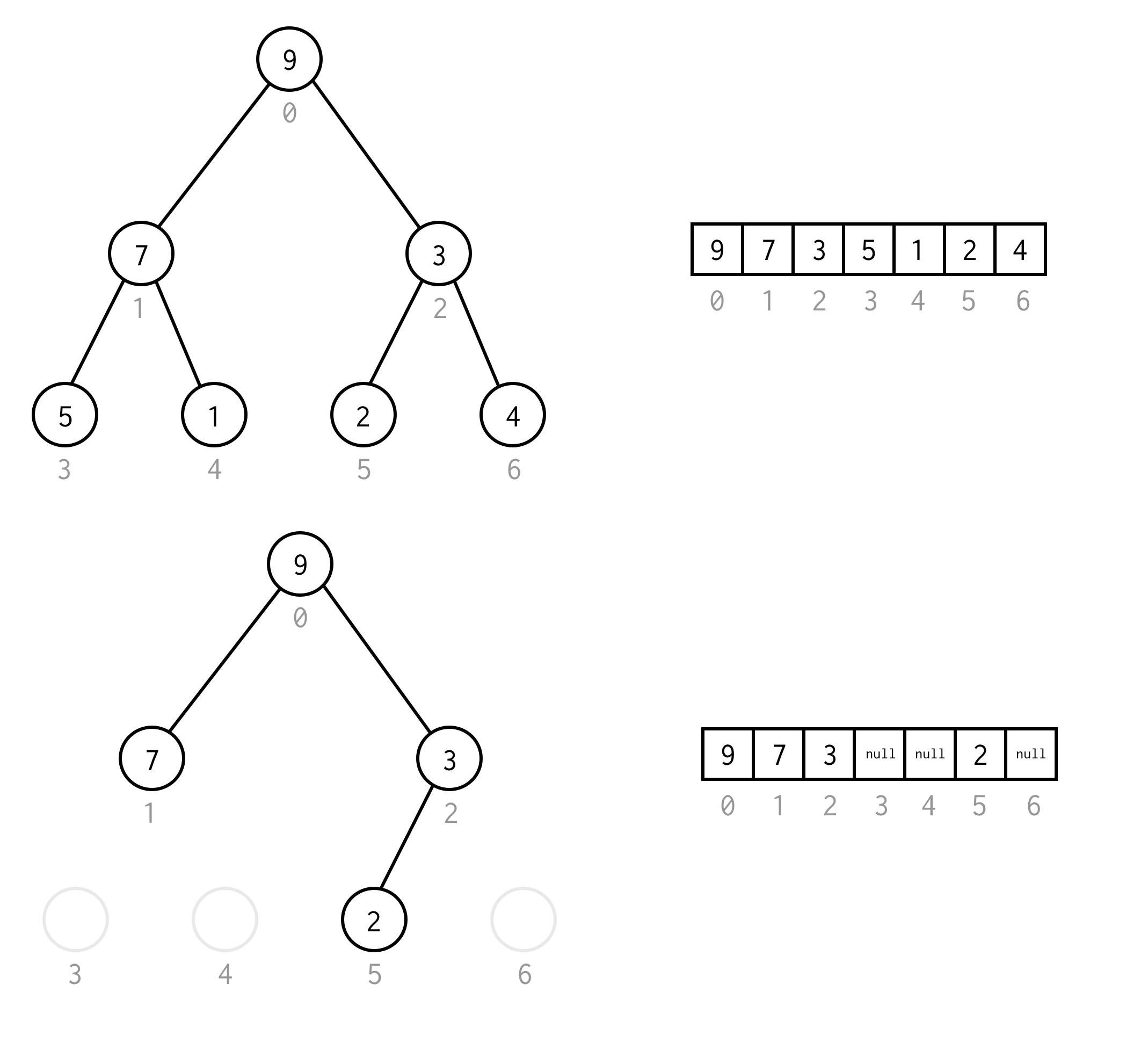
Esta representación de array para el árbol binario la llamaremos Binary Tree Array.Siempre asumimos que contendrá elementos.

BFS vs DFS

Existen dos algoritmos de búsqueda para el árbol binario: la búsqueda en profundidad (breadth-first search, BFS) y la búsqueda en profundidad (depth-first search, DFS).

La mejor manera de entenderlos es visualmente

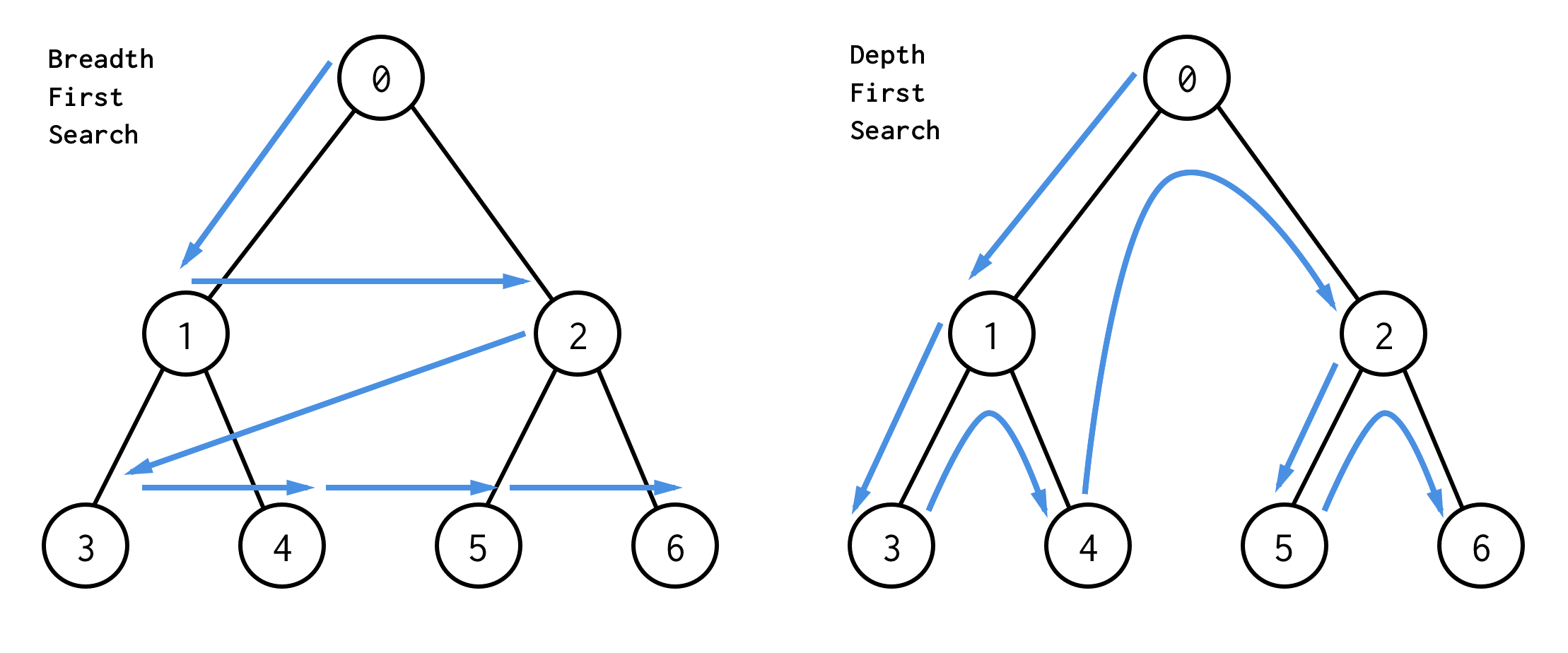
El BFS busca los nodos nivel a nivel, empezando por el nodo raíz. Luego comprobando sus hijos. Hasta que se procesan todos los nodos o se encuentra el nodo que satisface la condición de búsqueda.

DFS se comporta de forma diferente. Comprueba todos los nodos desde el camino más a la izquierda desde la raíz a la hoja, luego salta hacia arriba y comprueba el nodo de la derecha y así sucesivamente.

Para los árboles binarios clásicos BFS implementado utilizando la estructura de datos de cola (LinkedList implementa la cola)

public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}

Si reemplaza la cola con la pila obtendrá la implementación DFS.

public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}

Por ejemplo, suponga que necesita encontrar un nodo con valor 1 en el siguiente árbol.

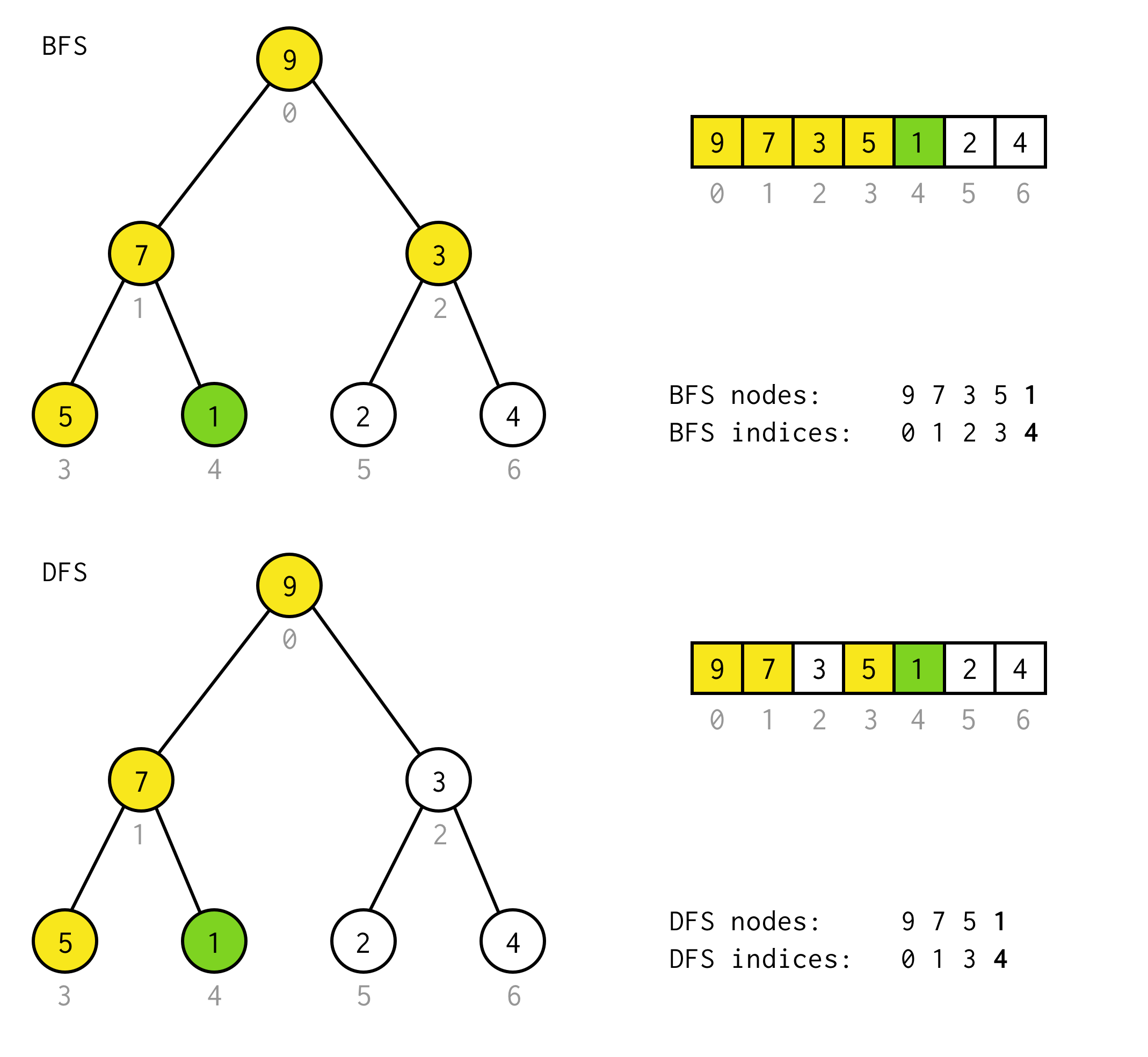
Las celdas amarillas son celdas que se prueban en el algoritmo de búsqueda antes de encontrar el nodo necesario.Tenga en cuenta que para algunos casos DFS requiere menos nodos para el procesamiento.Para algunos casos requiere más.

BFS y DFS para la matriz de árbol binario

La búsqueda en profundidad para la matriz de árbol binario es trivial.Dado que los elementos en la matriz de árbol binario se colocan nivel por nivel ybfs también está comprobando el elemento nivel por nivel, bfs para la matriz de árbol binario es sólo la búsqueda lineal

public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}

La búsqueda en profundidad es un poco más difícil.

Usando la estructura de datos de la pila se podría implementar de la misma manera que para el árbol binario clásico, sólo hay que poner los índices en la pila.

Desde este punto la recursividad no es diferente en absoluto, sólo se utiliza la pila de llamadas a métodos implícitos en lugar de la pila de la estructura de datos.

¿Qué pasaría si pudiéramos implementar el DFS sin pila ni recursividad.Al final es sólo una selección del índice correcto en cada paso?

Bueno, vamos a intentarlo.

DFS para Binary Tree Array (sin pila y recursividad)

Como en el BFS empezamos desde el índice raíz 0.
Entonces necesitamos inspeccionar su hijo izquierdo, cuyo índice podría ser calculado por la fórmula 2*i+1.
Llamemos al proceso de ir al siguiente hijo izquierdo duplicando.

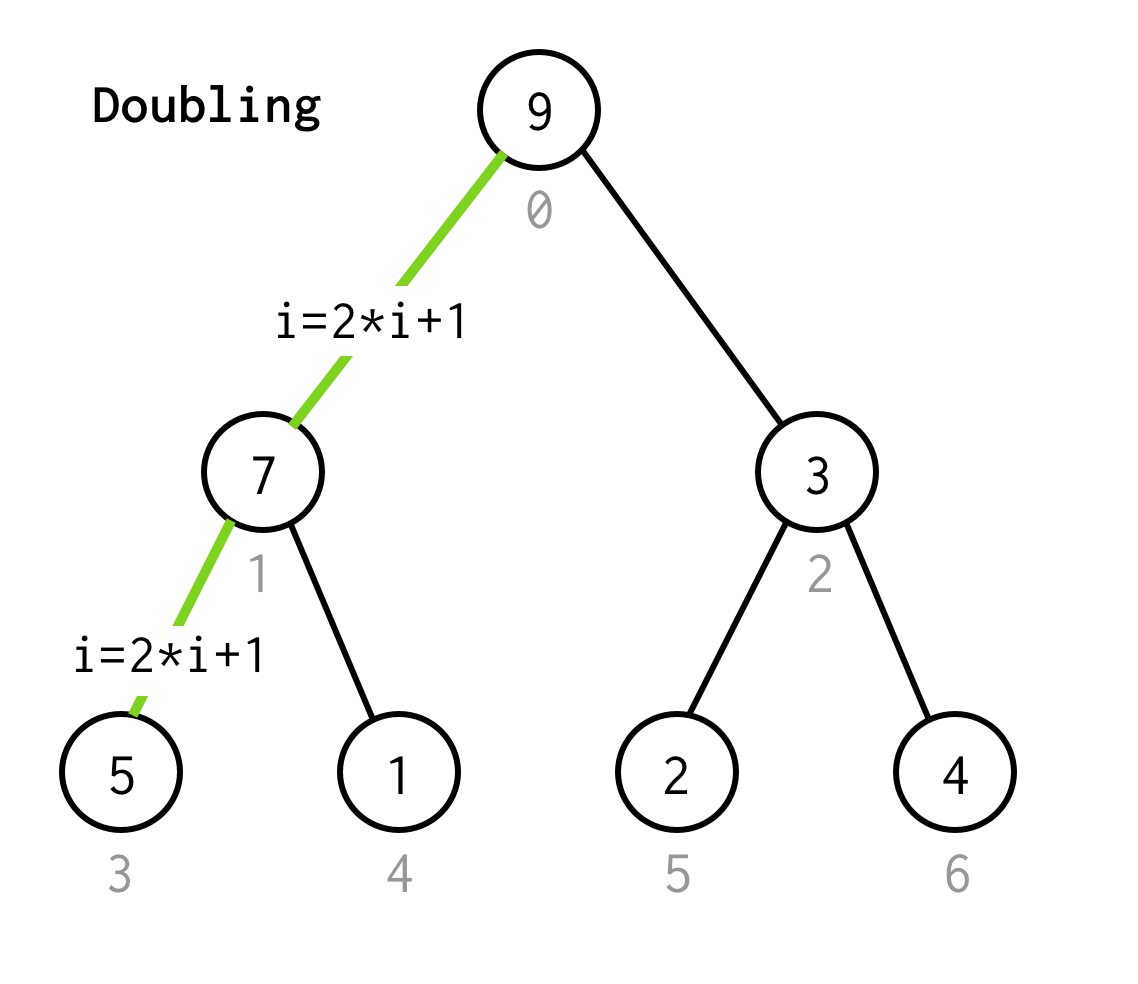
Continuamos duplicando el índice hasta que no paremos en el nodo hoja.

¿Entonces cómo podemos entender que es un nodo hoja?

Si el siguiente hijo de la izquierda produce una excepción de índice fuera de los límites del array, tenemos que dejar de duplicar y saltar al hijo de la derecha.

Esa es una solución válida, pero podemos evitar la duplicación innecesaria.La observación aquí es que el número de elementos en el árbol de unos height es dos veces mayor (y más uno)que el árbol con height - 1.

Para el árbol con height = 2 tenemos 7 elementos, para el árbol con height = 3 tenemos 7*2+1 = 15 elementos.

Usando esta observación construimos la condición simple

i < array.length / 2

Podemos comprobar que esta condición es válida para cualquier nodo no hoja del árbol.

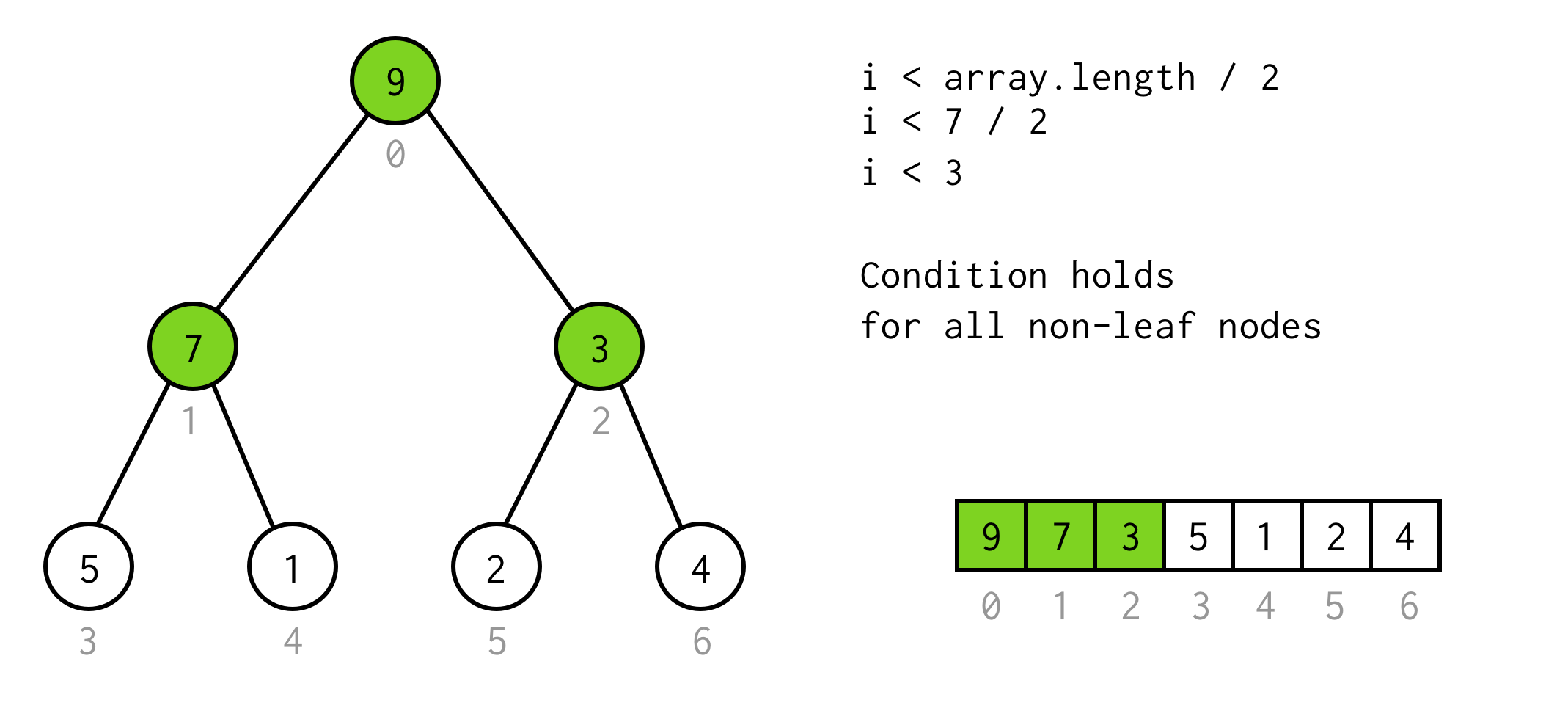
Bien hasta aquí. Podemos ejecutar la duplicación, e incluso sabemos cuándo parar.Pero de esta manera podemos comprobar sólo los hijos izquierdos de los nodos.

Cuando nos atascamos en el nodo hoja y no podemos aplicar la duplicación más, realizamos la operación de salto.Básicamente, si la duplicación es ir al hijo izquierdo, el salto es ir al padre e ir al hijo derecho.

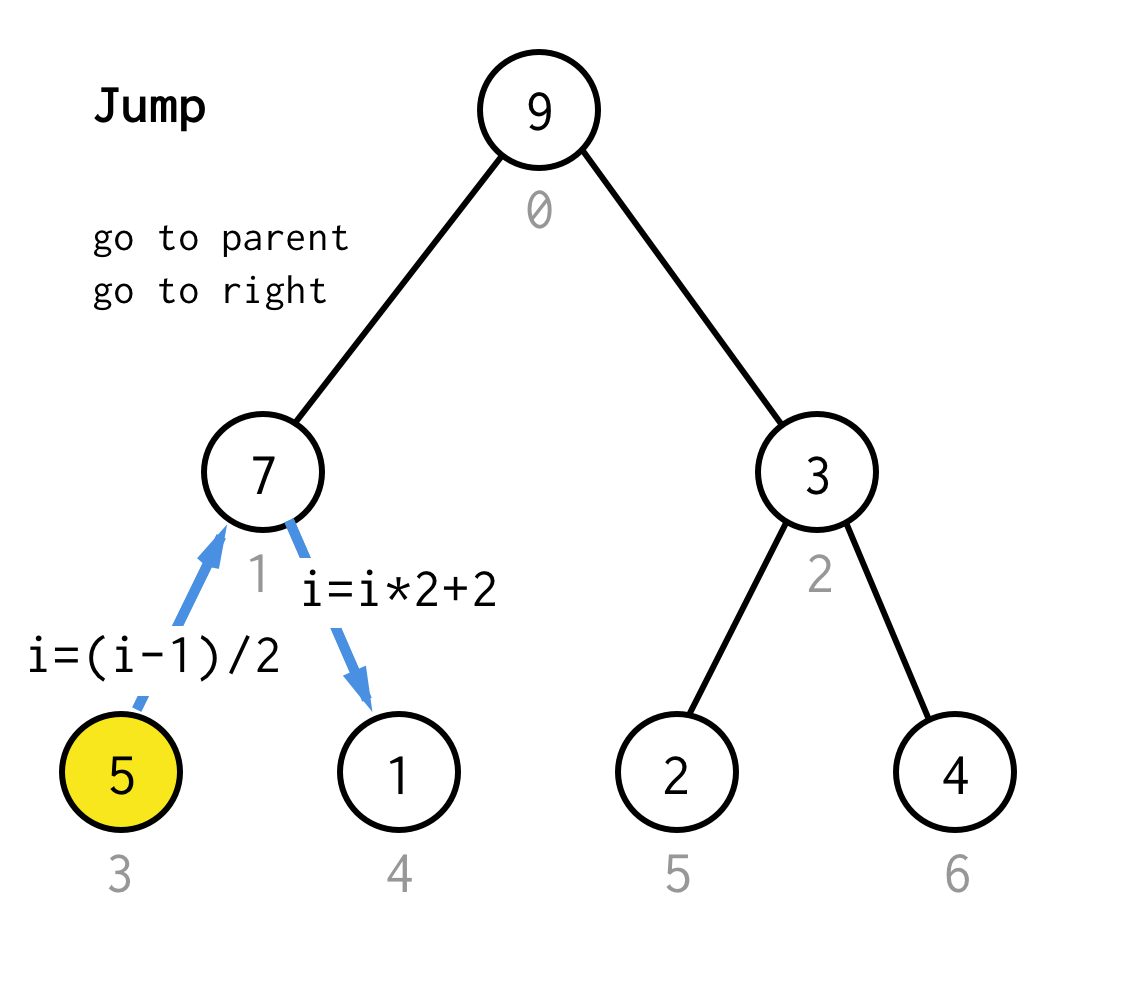
Esta operación de salto puede implementarse simplemente incrementando el índice de la hoja.Pero cuando nos quedamos atascados en el siguiente nodo de la hoja, el incremento no mueve el nodo al siguiente nodo, requerido por DFS.Así que tenemos que hacer doble salto

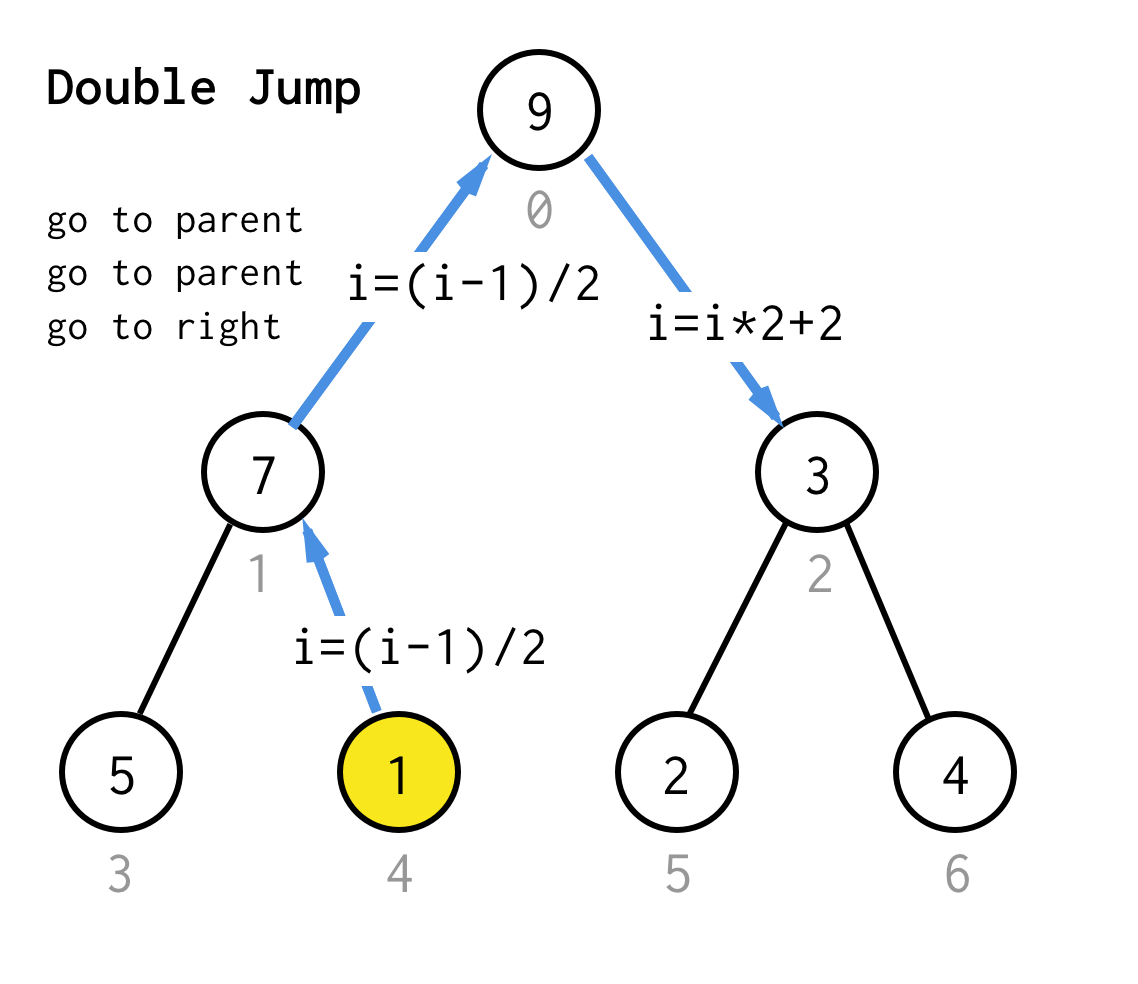
Para hacerlo más genérico, para nuestro algoritmo podríamos definir la operación salto N, que especifica cuántos saltos al padre requiere y siempre termina con un salto al hijo correcto.

Para el árbol con altura 1, necesitamos un salto, el salto 1

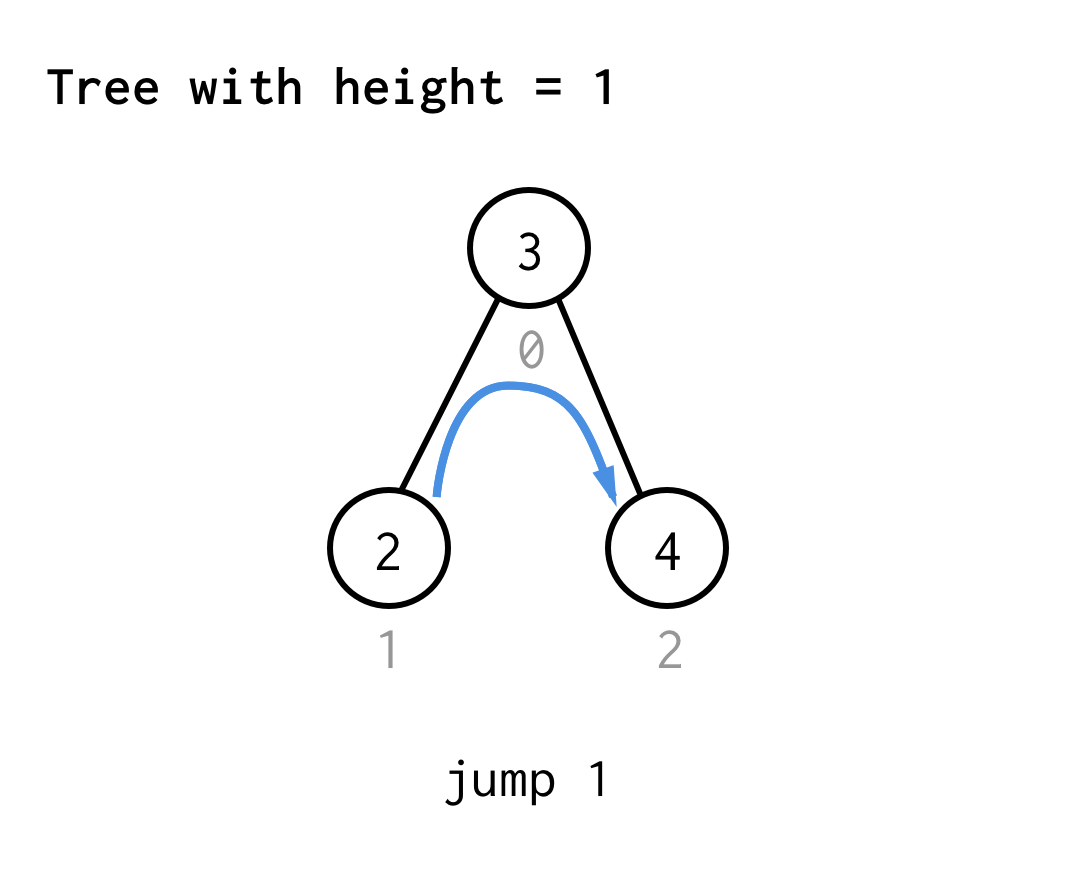
Para el árbol con altura 2, necesitamos un salto, un salto doble, y que un salto de nuevo

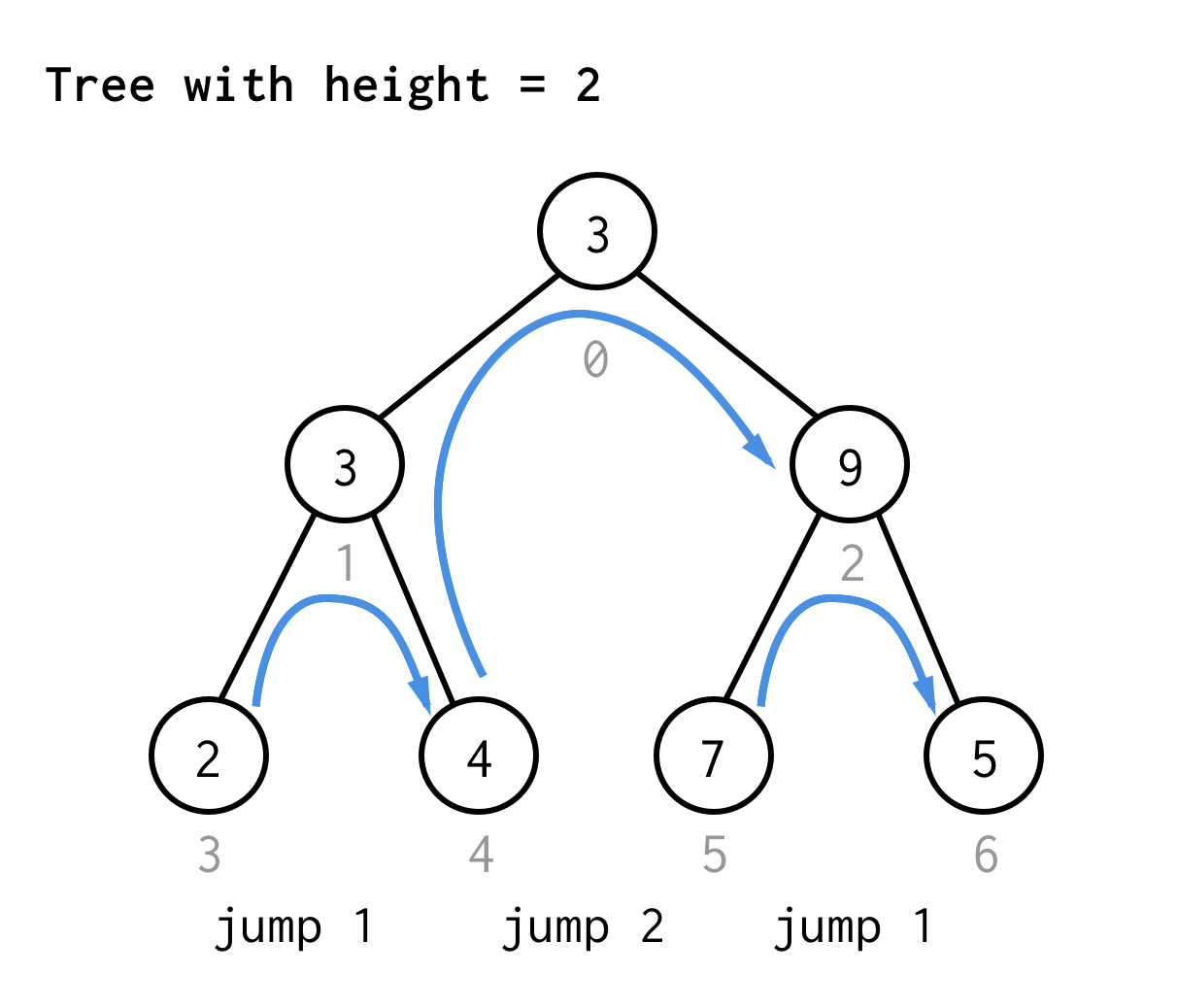
Para el árbol con altura 3, se pueden aplicar las mismas reglas y obtener 7 saltos.

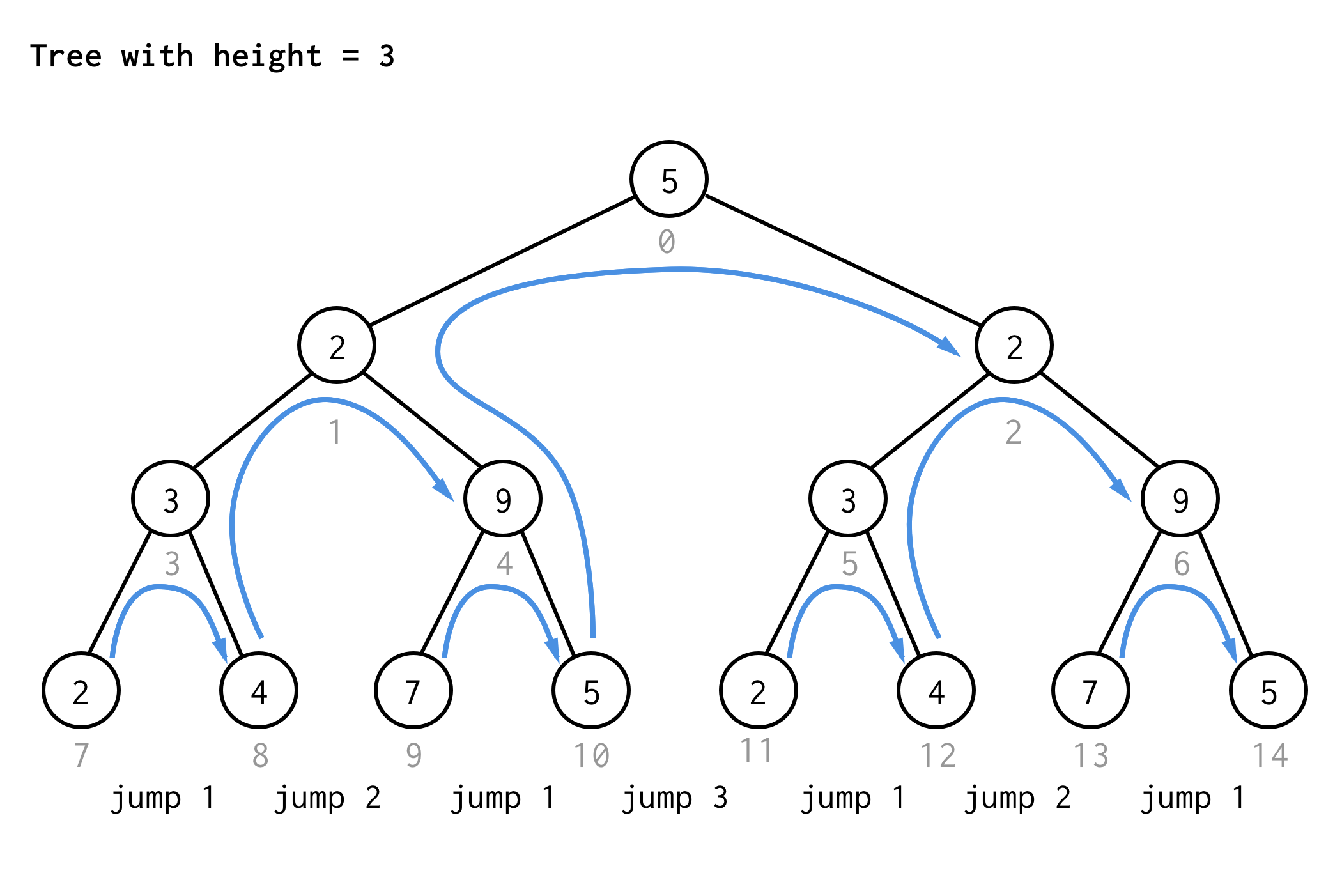
¿Ves el patrón?

Si aplicas la misma regla al árbol de altura 4 y escribes sólo los valores de los saltos obtendrás el siguiente número de secuencia

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

Esta secuencia se conoce como palabras Zimin y tiene definición recursiva, lo cual no es bueno, porque no se nos permite usar la recursión.

Busquemos otra forma de calcularla.

Si observamos con atención la secuencia de saltos, podemos ver un patrón no recursivo.

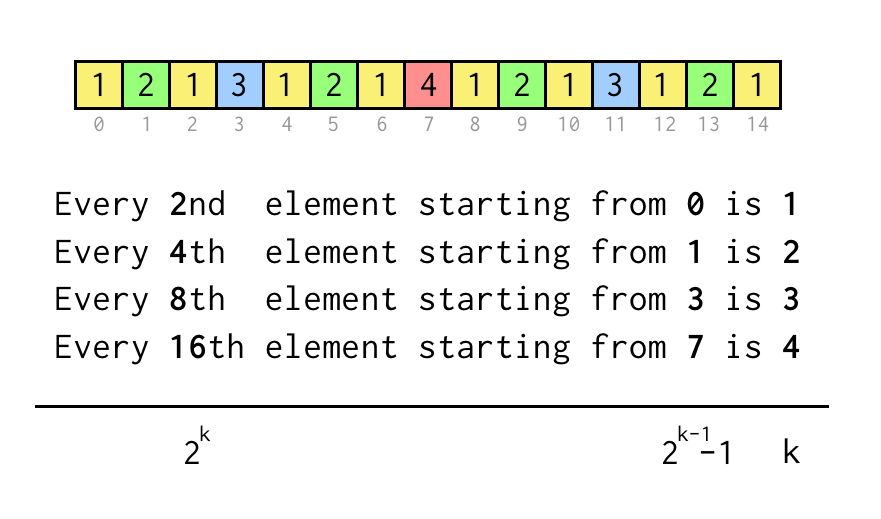
Podemos rastrear el índice de la hoja actual j, que corresponde al índice de la matriz de la secuencia anterior.

Para verificar la declaración como «Cada 8 elementos a partir de 3» sólo comprobamos j % 8 == 3, si es cierto tres saltos al nodo padre requerido.

El proceso de salto iterativo será el siguiente

• Empezar con k = 1
• Saltar una vez al padre aplicando i = (i - 1)/2
• Si leaf % 2*k == k - 1 todos los saltos realizados, salir
• De lo contrario, poner k a 2*k y repetir.

Si se pone todo lo que hemos discutido

public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}

Hecho. DFS para array de árbol binario sin pila y recursión

Complejidad

La complejidad parece cuadrática porque tenemos bucle dentro de un bucle, pero veamos cuál es la realidad.

• Para la mitad de los nodos totales (n/2) utilizamos la estrategia de duplicación, que es constante O(1)
• Para la otra mitad de los nodos totales (n/2) utilizamos la estrategia de salto de hoja.
• La mitad de los nodos de salto de hoja (n/4) requieren sólo un salto de padre, 1 iteración. O(1)
• La mitad de esta mitad (n/8) requieren dos saltos, o sea 2 iteraciones. O(1)
• …
• Sólo un nodo de salto de hoja requiere un salto completo a la raíz, que es O(logN)
• Entonces, si todos los casos tiene O(1) excepto uno que es O(logN), podemos decir que el promedio de salto es O(1)
• La complejidad total es O(n)

Rendimiento

Aunque la teoría es buena, veamos cómo funciona este algoritmo en la práctica, comparándolo con otros.

Probamos 5 algoritmos, usando JMH.

• BFS en árbol binario (lista enlazada como cola)
• BFS en array de árbol binario (búsqueda lineal)
• DFS en árbol binario (pila)
• DFS en Array de Árboles Binarios (pila)
• DFS iterativo en Array de Árboles Binarios

Hemos precreado un árbol y usado el predicado para acertar el último nodo,para asegurarnos de que siempre golpeamos el mismo número de nodos para todos los algoritmos.

Entonces, resultados

Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/s

Obviamente, BFS en array gana. Es sólo una búsqueda lineal, así que si puedes representar el árbol binario como array, hazlo.

El DFS iterativo, que acabamos de describir en el artículo, ocupa el segundo lugar y es 4.5 veces más lento que la búsqueda lineal (BFS sobre array)

El resto de los tres algoritmos son incluso más lentos que el DFS iterativo, probablemente, porque implican estructuras de datos adicionales, espacio extra y asignación de memoria.

Y el peor caso es el BFS sobre árbol binario. Sospecho que aquí la lista enlazada es un problema.

Conclusión

La matriz de árbol binario es un buen truco para representar la estructura de datos jerárquica como una matriz estática (región contigua en la memoria). Define una relación de índice simple para moverse de padre a hijo, así como para moverse de hijo a padre, lo que no es posible con la representación clásica de matriz binaria. Existen algunos inconvenientes, como la lentitud en la inserción/eliminación, pero estoy seguro de que hay muchas aplicaciones para los arrays binarios.

Como hemos demostrado, los algoritmos de búsqueda, BFS y DFS implementados en arrays son mucho más rápidos que sus hermanos en una estructura basada en referencias. Para los problemas del mundo real no es tan importante, y, probablemente, seguiré utilizando la matriz binaria basada en referencias.

De todos modos, fue un buen ejercicio. Esperar la pregunta «DFS en matriz binaria sin recursividad y la pila» en su próxima entrevista.

• algoritmos
• datastructures
• programación

mishadoff 10 de septiembre de 2017