Privacidad &Cookies
Este sitio utiliza cookies. Al continuar, aceptas su uso. Obtenga más información, incluyendo cómo controlar las cookies.
Una espiral es una curva que «emana de un punto, alejándose a medida que gira alrededor del punto».

Hay muchos tipos diferentes de espirales dependiendo de las fórmulas que las crean. En esta entrada del blog, hablaré de las espirales bidimensionales (ten en cuenta que también existe una variedad de espirales tridimensionales).
Espiral de Arquímedes
Se trata de una espiral que lleva el nombre del famoso matemático griego Arquímedes, que fue el primero en describirla en su libro Sobre las espirales. Se describe mediante la siguiente ecuación polar:
donde a y b son números reales.
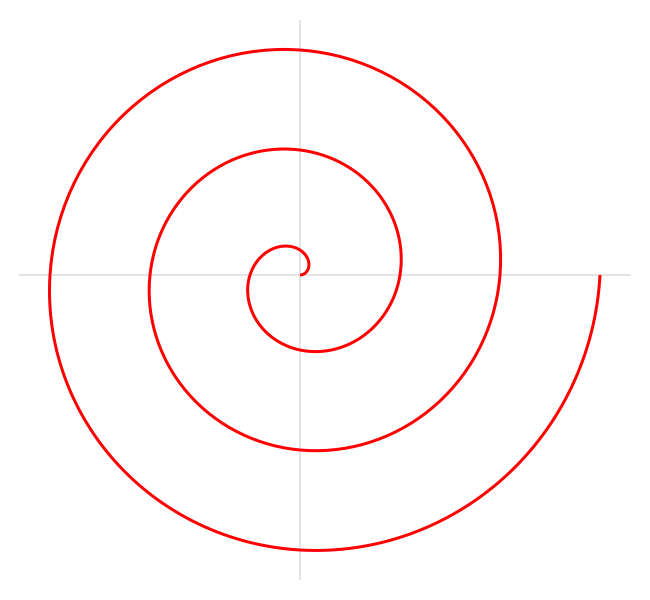
Al cambiar el parámetro a la espiral girará y el parámetro b controla la distancia entre giros sucesivos.
Espiral de Fermat
La espiral de Fermat es una espiral parabólica que obedece a la siguiente ecuación polar:
Es un tipo de espiral arquimediana.

Espiral de Euler
También conocida como espiral de Cornu, es una curva cuya curvatura crece al aumentar la distancia al origen; «la curvatura de una curva circular es igual al recíproco del radio».

La forma paramétrica consta de dos ecuaciones con intervalos de Fresnel, que sólo pueden resolverse de forma aproximada.
Estas integrales, y por tanto la espiral de Euler, pueden utilizarse para describir la distribución de energía de la difracción de Fresnel en una única rendija en la teoría de ondas.
Espiral hiperbólica
Concebida por primera vez por Pierre Varignon en 1704, la espiral hiperbólica es una curva trascendental, lo que significa que «es una función analítica que no satisface una ecuación polinómica». Es lo contrario de una espiral arquimediana y, por tanto, tiene la siguiente ecuación polar:
En el centro, está a una distancia infinita del polo; para θ que empieza en 0, r empieza en el infinito.
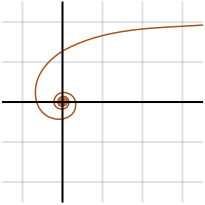
Lituus
El lituus es una espiral con una ecuación polar:
donde k es una constante. Por lo tanto, el ángulo es inversamente proporcional al cuadrado del radio. 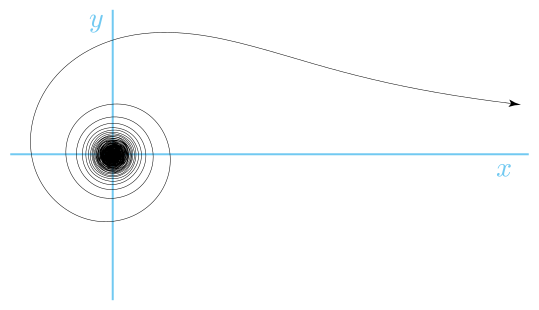
La curva recibió el nombre del antiguo lituus romano (un bastón augural curvado o trompeta de guerra) de Roger Cotes en una colección de artículos publicados en 1722.
Espiral logarítmica
 La espiral logarítmica es una espiral autosimilar, que aparece a menudo en la naturaleza. Fue descrita por primera vez por Descartes, pero fue estudiada en profundidad por Jacob Bernoulli, que la llamó «la espiral maravillosa». Tiene unas ecuaciones polares de
La espiral logarítmica es una espiral autosimilar, que aparece a menudo en la naturaleza. Fue descrita por primera vez por Descartes, pero fue estudiada en profundidad por Jacob Bernoulli, que la llamó «la espiral maravillosa». Tiene unas ecuaciones polares de





Deja una respuesta