Eigenvector

Los vectores propios son un conjunto especial de vectores asociados a un sistema lineal de ecuaciones (i.e., una ecuación matricial) que a veces también se conocen como vectores característicos, vectores propios o vectores latentes (Marcus y Minc 1988, p. 144).

La determinación de los vectores propios y de los valores propios de un sistema es extremadamente importante en física e ingeniería, donde equivale a la diagonalización de matrices y surge en aplicaciones tan comunes como el análisis de estabilidad, la física de los cuerpos en rotación y las pequeñas oscilaciones de los sistemas vibratorios, por nombrar sólo algunas. A cada vector propio le corresponde un valor propio. Matemáticamente, hay que distinguir dos tipos diferentes de vectores propios: vectores propios izquierdos y vectores propios derechos. Sin embargo, para muchos problemas de física e ingeniería, basta con considerar sólo los vectores propios derechos. Por lo tanto, el término «eigenvector» utilizado sin calificación en tales aplicaciones puede entenderse que se refiere a un eigenvector derecho.

La descomposición de una matriz cuadrada en valores propios y vectores propios se conoce en este trabajo como descomposición de los eigen, y el hecho de que esta descomposición sea siempre posible siempre que la matriz formada por los eigenvectores de sea cuadrada se conoce como teorema de la descomposición de los eigen.

Define un vector propio derecho como un vector columna que satisface

(1)

donde es una matriz, así que

(2)

lo que significa que los valores propios de la derecha deben tener determinante cero, es decire.,

(3)

De manera similar, defina un vector propio izquierdo como un vector fila que satisface

(4)

Tomando la transposición de cada lado se obtiene

(5)

que puede reescribirse como

(6)

Regula de nuevo para obtener

(7)

lo que significa

(8)

La reescritura da

			(9)
			(10)
			(11)

donde el último paso se deduce de la identidad

(12)

La equiparación de las ecuaciones (◇) y (11), que son ambas iguales a 0 para y arbitrarias, requiere por tanto que , es decir, los valores propios de la izquierda y de la derecha son equivalentes, afirmación que no es cierta para los vectores propios.

Sea una matriz formada por las columnas de los vectores propios de la derecha y una matriz formada por las filas de los vectores propios de la izquierda. Sea

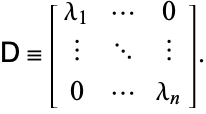(13)

Entonces

			(14)
			(15)

y

			(16)
			(17)

así

(18)

Pero esta ecuación es de la forma

(19)

donde es una matriz diagonal, por lo que debe ser cierto que también es diagonal. En particular, si es una matriz simétrica, entonces los vectores propios izquierdo y derecho son simplemente la transposición de cada uno, y si es una matriz autoadjunta (es decir, es hermitiana), entonces los vectores propios izquierdo y derecho son matrices adjuntas.

Los vectores propios pueden no ser iguales al vector cero. Un múltiplo escalar no nulo de un vector propio es equivalente al vector propio original. Por lo tanto, sin pérdida de generalidad, los vectores propios se normalizan a menudo a la unidad de longitud.

Mientras que una matriz siempre tiene valores propios, algunos o todos los cuales pueden ser degenerados, tal matriz puede tener entre 0 y vectores propios linealmente independientes. Por ejemplo, la matriz sólo tiene el único vector propio .

Los vectores propios pueden calcularse en Wolfram Language utilizando Eigenvectores. Este comando siempre devuelve una lista de longitud , por lo que cualquier vector propio que no sea linealmente independiente se devuelve como vector cero. Los vectores propios y los valores propios pueden devolverse juntos utilizando el comando Eigensystem.

Dada una matriz con los vectores propios , , y y los correspondientes valores propios , , y , entonces un vector arbitrario puede escribirse

(20)

Aplicando la matriz ,

			(21)
			(22)

así

(23)

Si , y , se deduce por tanto que

(24)

por lo que la aplicación repetida de la matriz a un vector arbitrario resulta sorprendentemente en un vector proporcional al vector propio con mayor valor propio.